1. 서 론
우리 나라에서도 최근에 규모가 큰 지진이 발생하였다. 2016년에는 경주 지역에서 5.8 규모의 지진이, 2017년에는 포항 지역에서는 5.4 규모의 지진으로 인하여 인적, 재산적 피해가 발생하였다. 이러한 지진 규모도 피해 규모에 직접적인 연관이 있지만, 지반 특성에 따라 지반 진동이 증폭 되거나 감쇠 되기도 하기 때문에 지반과 상하부 구조물과의 상호 작용에 대한 분석도 중요하다.
말뚝의 자유진동은 지진, 바람, 기계진동과 같은 동적 하중을 받는 말뚝지지 구조물의 설계 시 중요한 고려사항이다. 외부 가진력의 진동수와 말뚝지지 구조물의 고유진동수가 일치할 경우 진폭이 크게 증가하는 공진현상이 발생하여 말뚝과 상부구조물에 큰 손상을 초래할 수 있으므로 말뚝지지 구조물은 공진의 영향을 최소화하도록 설계한다. 말뚝지지 구조물 공진은 하부구조와 상부구조의 조합으로 결정되는데, 이를 위하여 하부구조와 상부구조물의 자유진동에 대한 연구가 필요하다.
그 동안 말뚝의 자유진동에 대한 많은 연구가 수행되었다. Prakash and Chandrasekaran(1977)은 탄성지반에 의해 수평방향으로 지지된 말뚝의 기본진동수(fundamental frequency)에 대한 수치해를 산정하였다. Ragab and Aggour(1986)은 상단 집중질량을 갖는 말뚝의 자유진동 특성을 평가하였고, Valsangkar and Pradhanang(1987)은 수직하중을 받는 부분매립 말뚝의 고유진동수에 대한 정확해를 산정하였다. Halabe and Jain(1996)은 자유진동하는 말뚝의 특성방정식을 유도하고 말뚝의 고유진동수와 모드형상을 분석하였다. Hu et al.(2008)은 지반의 비선형거동을 고려한 말뚝의 자유진동 해석을 수행하였다. Catal(2008)과 Yesilce(2011)는 미분변환법(differential transform method)과 미분구적요소법(differential quadrature element method)을 각각 적용하여 수직재하 말뚝의 고유진동수를 산정하였다. 최근에 Ma et al.(2018)은 지반의 전단특성이 말뚝의 자유진동에 미치는 영향을 평가하였다.
기존 연구에서는 말뚝의 자유진동 거동에 관한 다양한 연구가 수행되었으나, 이들은 모두 등단면 원통형 말뚝을 대상으로 하였다. 그러나 말뚝의 하중전이특성과 그에 필요한 말뚝의 최적단면을 고려할 때 말뚝의 두부에서 선단으로 갈수록 말뚝의 단면이 작아지는 테이퍼 말뚝이 원통형 말뚝보다 구조적 안정성과 경제성이 우수하여 현장에서 많이 적용되고 있다(El Naggar and Wei, 1999; Paik and Lee, 2008). 또한 기존 연구는 상부하중으로 인해 말뚝 주면에 발생하는 상향 저항력을 고려하지 않아 말뚝과 지반 사이의 주면마찰력이 말뚝의 자유진동에 미치는 영향에 대한 정량적 평가가 이루어지지 않았다.
이 논문은 불균질 지반에 설치된 정적 수직하중을 받는 테이퍼 마찰말뚝의 자유진동을 연구하는데 그 목적이 있다. 이를 위해 말뚝-지반 시스템의 자유진동을 지배하는 상미분방정식과 경계조건을 유도하였다. 깊이 방향으로 단면이 일정한 원통형 말뚝에 대한 고유진동수의 수치해를 문헌값과 비교하여 제안된 해석모델의 타당성을 검증하였다. 또한, 말뚝과 지반에 관련된 무차원 변수들이 테이퍼 말뚝의 고유진동수와 모드형상에 미치는 영향을 분석하였다.
2. 말뚝-지반 시스템
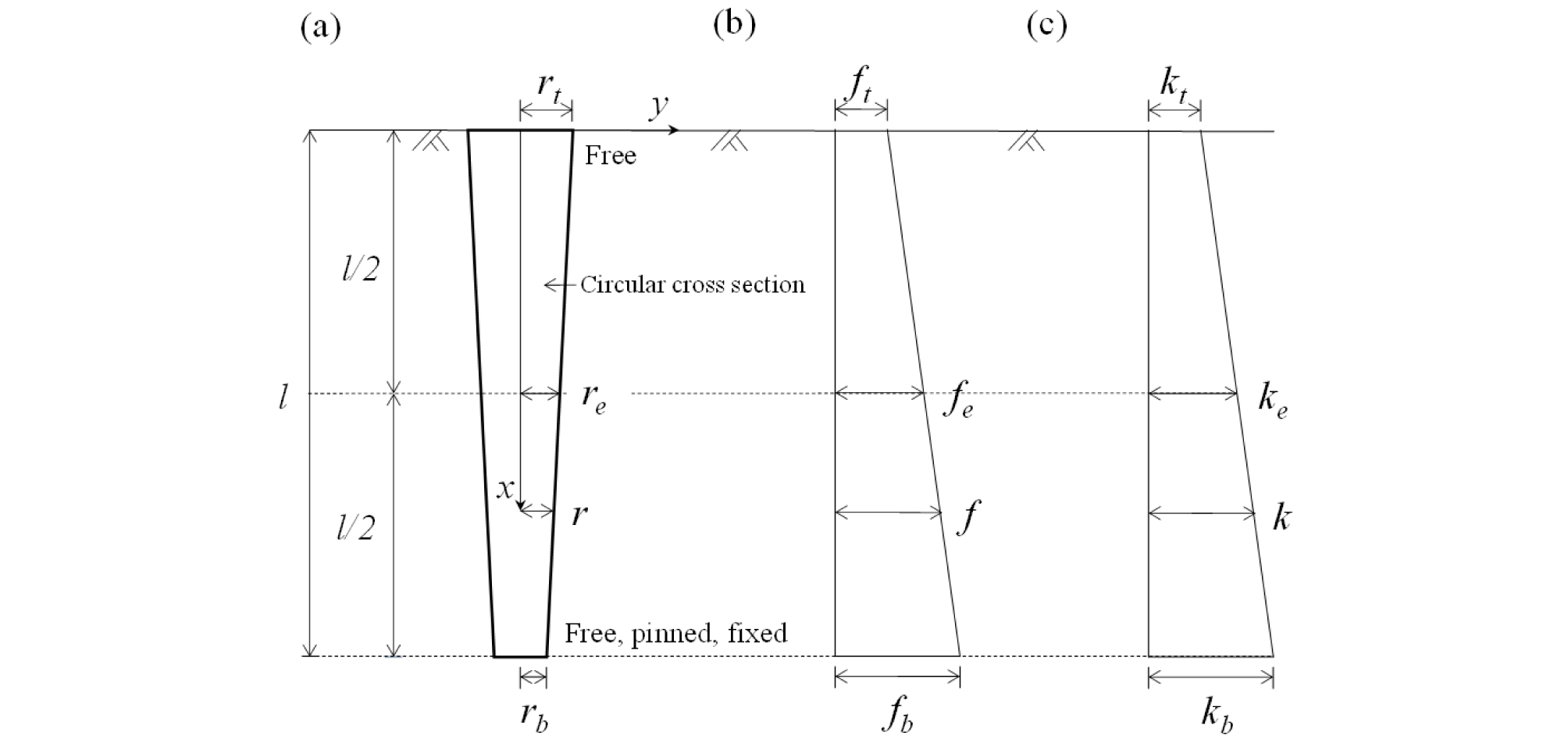
Fig. 1에서는 불균질한 탄성지반 속에 설치된 테이퍼 마찰말뚝의 자유진동 해석을 위한 변수들을 그림으로 표시하였다. Fig. 1(a)에서는 말뚝의 형상에 대한 변수를 나타냈으며, 말뚝길이는 이고, 일반적인 테이퍼 마찰말뚝과 같이 단면은 원형으로 깊이가 증가함에 따라 반경은 선형적으로 감소한다고 가정하였다. Fig. 1(a)와 같이 말뚝두부 x=0에서 말뚝의 반경은 rt이고 말뚝선단 x=l에서는 rb이다. 말뚝중앙에서 반경 re는 rt와 rb의 평균이다.
말뚝중앙에서 말뚝의 직경 we, 원주길이 ue, 단면적 Ae, 단면이차모멘트 Ie는 식 (1)과 같다.
| $$w_e=2r_e,\;\;u_e=2\pi\;r_e,\;\;A_e=\pi r_e^2,\;\;I_e=\pi r_e^4⁄4$$ | (1) |
테이퍼 마찰말뚝의 단면비 ar은 하단의 반지름 rb과 상단의 반지름 rt의 비로 정의한다.
| $$a_r=\frac{r_b}{r_t}$$ | (2) |
이로부터 말뚝 깊이 x에서 반경 r은 다음과 같은 선형식으로 표현할 수 있다.
| $$r=r_t―(r_t―r_b)\;x/l=\frac{2r_e}{m_r}\;H_x$$ | (3) |
여기서 mr=ar+1, Hx=1+nr(x/l), nr=ar-1이다. 이와 유사하게 말뚝 깊이 x에서 직경, 원주길이 u, 단면적 A, 단면이차모멘트 I를 반경 re와 선형식 Hx로 정리하면 다음과 같다.
| $$w=\frac{4r_e}{m_r}\;H_x,\;u=\frac{4\pi r_e}{m_r}H_x,\;\;A=\frac{4\pi r_e^2}{m_r^2}\;H_x^2,\;\;I=\frac{4\pi r_e^4}{m_r^4}\;H_x^4$$ | (4) |
Fig. 1(b)는 수직압축하중을 받는 말뚝의 주면에 발생하는 단위극한주면마찰력(unit skin ultimate friction resistance)을 나타내며 말뚝 깊이에 따라 선형적으로 변화한다(El Naggar and Wei, 1999). 말뚝의 두부와 선단에서 단위극한주면마찰력은 각각 ft와 fb이다. 말뚝중앙에서 단위주면마찰력 fe는 식 (5)와 같이 구할 수 있다.
| $$f_e=\frac12(f_t+f_b)$$ | (5) |
주면마찰력비 af는 식 (6)과 같이 정의하며,
| $$a_f=\frac{f_b}{f_t}$$ | (6) |
이로부터 깊이 x에서 주면마찰력 f는 다음과 같이 표현할 수 있다.
| $$f=\frac{2f_e}{m_f}S_x$$ | (7) |
여기서 mf=af+1, Sx=1+nf(x/l), nf=af-1이다.
Fig. 1(c)는 지반반력계수(coefficient of subgrade reaction) k를 나타내며 깊이 방향으로 선형적으로 변화한다(Reese and Van Impe, 2011). 말뚝의 두부와 선단에서 지반반력계수는 각각 kt와 kb이다. 말뚝중앙에서 지반반력계수 ke는 식 (8)과 같이 구할 수 있다.
| $$k_e=0.5(k_t+k_b)$$ | (8) |
불균질 지반특성은 다음과 같이 지반계수비 ak로 정의되며,
| $$a_k=\frac{k_b}{k_t}$$ | (9) |
이로부터 깊이 x에서 지반반력계수 k는 다음과 같이 표현할 수 있다.
| $$k=\frac{2k_e}{m_k}Q_x$$ | (10) |
여기서 mk=ak+1, Qx=1+nk(x/l), nk=ak-1이다.
테이퍼 마찰말뚝의 자유진동 특성을 분석하기 위하여, 말뚝의 경계조건은 Fig. 1(a)에 나타낸 바와 같이 말뚝두부(x=0)는 자유(free)로 고정하고, 말뚝선단(x=l)은 자유, 회전(pinned), 고정(fixed)으로 가정하여 해석하였다.
3. 수학적 정식화
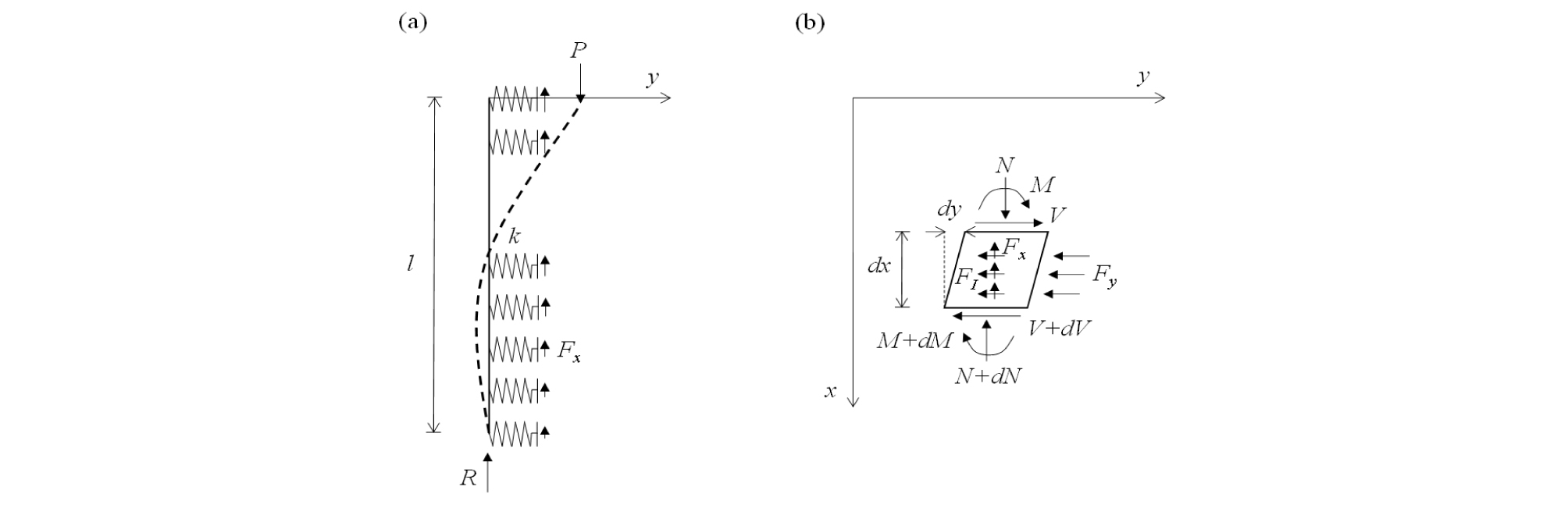
Fig. 2(a)는 자유진동하는 말뚝의 동적 변위의 예를 직교좌표계 (x,y)에 나타내었다. 말뚝의 자유진동은 조화진동(harmonic motion)으로 동적 변위는 깊이와 시간에 따라 y(x,t)=ysin(ωit)로 표현된다. 여기서, y는 진폭, ωi는 고유각진동수, i는 모드번호, t는 시간이다. 본 연구에서는 정적 압축하중이 자유진동에 미치는 영향을 분석하기 위하여 수직방향 외력 P가 말뚝두부에 작용하며 이로 인해 말뚝의 주면과 선단에는 주면마찰력 Fx와 상향반력 R이 각각 발생한다. 말뚝의 변위 y에 저항하는 지반반력 Fy와 질량을 갖는 말뚝요소의 수평방향 관성력 FI가 y의 반대 방향으로 발생한다. 말뚝 내부에는 축방향력 N, 전단력 V, 휨 모멘트 M의 합응력들이 작용한다.
Fig. 2(b)는 미소길이 dx를 갖는 말뚝요소의 자유물체도를 직교좌표계 (x,y)에 나타낸 것이다. 이 요소에는 내력 N, V, M, F1, 외력 Fx, Fy가 작용하여 평형상태에 있다. 이 자유물체도를 이용하여 ΣFx=0, ΣFy=0, ΣM=0의 평형방정식을 구하면 식 (11)∼(13)과 같다.
| $$\frac{dN}{dx}+F_x=0$$ | (11) |
| $$\frac{dV}{dx}+F_y+F_I=0$$ | (12) |
| $$\frac{dM}{dx}-V+N\;\frac{dy}{dx}=0$$ | (13) |
식 (11)∼(13)에서 Fx, Fy, FI는 각각 식 (14)∼(16)과 같이 주어진다(Gabr et. al., 1994; Humar, 1990).
| $$F_x=fu$$ | (14) |
| $$F_y=kwy$$ | (15) |
| $$F_I=―\rho A\omega_i^2y$$ | (16) |
말뚝요소에 대한 다음의 휨-변위 관계식(Goodno and Gere, 2018)은 다음과 같다.
| $$M=EI\;\frac{d^2y}{dx^2}$$ | (17) |
식 (17)을 식 (11)∼(16)과 조합하여 풀면 다음과 같은 4계 상미분방정식을 얻는다.
| $$EI\frac{d^4y}{dx^4}+2E\frac{dI}{dx}\frac{d^3y}{dx^3}+\left(E\frac{d^2I}{dx^2}+N\right)\frac{d^2y}{dx^2}―fu\frac{dy}{dx}+(kw―\rho A\omega_i^2)y=0$$ | (18) |
여기서 E는 말뚝의 탄성계수이고, N은 말뚝 내 축방향력으로 다음과 같이 표현할 수 있다.
| $$N=P-\int_0^xfudx$$ | (19) |
식 (19)에 식 (4)와 식 (7)을 대입하여 적분하면 다음과 같이 정리된다.
| $$N=P-\frac{8\pi r_ef_el}{m_rm_f}T_x$$ | (20) |
여기서 이며, 깊이 x=l에서 축방향력 Nx=l은 상향반력 R과 같다.
식 (18)을 무차원 식으로 유도하기 위하여 다음과 같은 무차원 변수를 도입한다.
| $$\eta=\frac yl,\;\;\xi=\frac xl,\;\;\gamma=\frac{w_e}l$$ | (21a) |
| $$\alpha=\frac l\lambda,\;\;beta=\frac{f_eu_e\lambda^3}{\pi EI_e},\;\;p=\frac{Pl^2}{\pi^2EI_e}$$ | (21b) |
| $$b=\frac{Bl^2}{\pi^2EI_e},\;\;C_i=\omega_il^2\sqrt{\frac{\rho A_e}{EI_e}}$$ | (21c) |
여기서 ξ와 η는 무차원 직교좌표계, γ는 직경비, α는 특성길이비, β는 주면마찰변수, p는 수직하중변수, b는 좌굴하중변수, Ci는 고유진동수변수이며, λ는 아래 식과 같이 정의한다. λ는 물리적으로 말뚝의 특성길이(characteristic length)를 의미하며 지반에 대한 말뚝의 상대강성으로 해석할 수 있다.
| $$\lambda=\sqrt[5]{\frac{EI_e}{k_e}}$$ | (22) |
식 (21)∼(22)를 식 (18)에 대입하고 식 (4), (7), (10), (20)을 이용하여 정리하면 다음과 같은 무차원 4계 상미분방정식을 얻을 수 있다.
여기서 이다.
지배 미분방정식의 경계조건을 다음과 같이 유도한다. 말뚝두부(x=0)은 자유이므로 휨 모멘트 M 및 전단력 V는 0이다. 이로부터 ξ=0에서 자유단의 경계조건을 다음과 같이 구할 수 있다.
| $$\frac{d^2\eta}{d\xi^2}=0$$ | (24) |
| $$d^3\eta/d\xi^3+\frac{\pi^2m_r^4p}{16}\frac{d\eta}{d\xi}=0$$ | (25) |
말뚝선단(x=l)은 자유 또는 회전 또는 고정이다. 자유단의 경우 x=l(ξ=1)에서 휨 모멘트 M 및 전단력 V는 0이므로 그 경계조건은 다음과 같다.
| $$\frac{d^2\eta}{d\xi^2}=0$$ | (26) |
| $$\frac{d^3\eta}{d\xi^3}+\frac{\pi^2m_r^3}{4a_r^4}\left[\frac{m_rp}4-\frac{\alpha^3\beta}{\pi m_f}\left(1\;+\;\frac{n_{r+n_f}}2+\frac{n_rn_f}3\right)\right]\frac{d\eta}{d\xi}=0$$ | (27) |
말뚝선단(x=l;ξ=1)의 회전단에서 변위 y 및 휨 모멘트 M은 0이므로 다음의 경계조건을 얻을 수 있다.
| $$\eta=0$$ | (28) |
| $$\frac{d^2\eta}{d\xi^2}=0$$ | (29) |
말뚝선단(x=l;ξ=1)의 고정단에서 변위 y 및 회전각 dy/dx는 0이므로 그 경계조건은 다음과 같다.
| $$\frac{d\eta}{d\xi}=0$$ | (30) |
4. 말뚝의 자유진동 해석
4.1 해석방법 및 검증
이상에서 불균질 탄성지반에 설치된 테이퍼 마찰말뚝의 자유진동 해석을 위한 지배방정식[식 (23)]과 경계조건식[식 (24)∼(30)]을 유도하였다. 지배방정식의 입력변수는 단면비 ar, 주면마찰력비 af, 지반계수비 ak, 직경비 γ, 특성길이비 α, 주면마찰변수 β, 수직하중변수 p이고, 입력변수에 의해 계산되는 상수는 mr=ar+1, nr=ar-1, mf=af+1, nf=af-1, mk=ak+1, nk=ak-1이다.
이로부터 얻어지는 지배방정식의 해는 말뚝의 고유진동수변수 Ci와 진동형상 (ξ, η)이다. 본 연구에서 미분방정식의 수치적분은 Runge-Kutta 법을 이용하여 직접 적분하였고, 미분방정식의 고유치(eigenvalue)인 Ci는 비선형방정식의 수치해법 중에 하나인 Regula-Falsi 법을 이용하여 계산하였다(Carnahan et al., 1969). 말뚝의 진동형상 (ξ, η)는 미분방정식의 수치적분의 결과로 산정된다. 이와 같은 말뚝-지반 시스템의 고유치 문제에 대한 해석절차는 Lee et al.(2014)의 문헌에서 그 적용성이 검증되었다.
Table 1은 원통형 선단지지말뚝의 고유각진동수 ωi를 나타내며 수치해 산정에 이용한 입력변수는 다음과 같다: l=10m, re=0.5m, fe=0, ke=98kN/m3, E=20GPa, ρ=2,300kg/m3, P=24MN (λ=6.31m, ar=1, ak=1, γ=0.1, α=1.58, β=0 and p=0.25). 말뚝 상단과 하단의 단부조건은 자유-자유와 회전-회전 조건으로 가정하였다. 해석모델의 검증을 위해 진동모드 i=1, 2, 3에 대한 본 해석과 문헌(Valsangkar and Pradhanang, 1987; Karovsky and Lebed, 2001)의 값을 함께 나타내었다. 이로부터 단부조건에 상관없이 두 고유진동수가 우수하게 근접하는 것을 확인할 수 있다.
Table 1. Comparison of natural frequencies for cylindrical end-bearing piles
| Data source | Natural frequency ωi (rad/s) | ||
| i=1 | i=2 | i=3 | |
| ● Free-free end | |||
| Valsangkar and Pradhanang (1987) | 7.372 | 143.7 | 438.5 |
| Present study | 7.366 | 143.7 | 438.5 |
| ● Pinned-pinned end | |||
| Valsangkar and Pradhanang (1987) | 63.15 | 281.2 | 645.3 |
| Karovsky and Lebed (2001) | 63.54 | 282.0 | 645.8 |
| Present study | 63.54 | 282.0 | 645.8 |
4.2 해석결과 및 토의
말뚝-지반 시스템의 재료 및 기하학적 특성이 고유진동수에 미치는 영향을 분석하기 위하여 다음과 같은 입력변수를 적용하였다: E=20GPa; re=0.5m; ke=10MN/m3. 이들 값으로 계산한 특성길이는 λ=2.5m이며, 이 경우 γα=0.4로 직경비 γ와 특성길이비 α는 서로 종속적인 관계를 갖는다. 해석결과는 실무에서 널리 적용되는 1차 모드(i=1)에 대한 기본진동수변수 Ci=1과 진동형상 (ξ,η)을 분석하였다(Carpinteri et al., 2014).
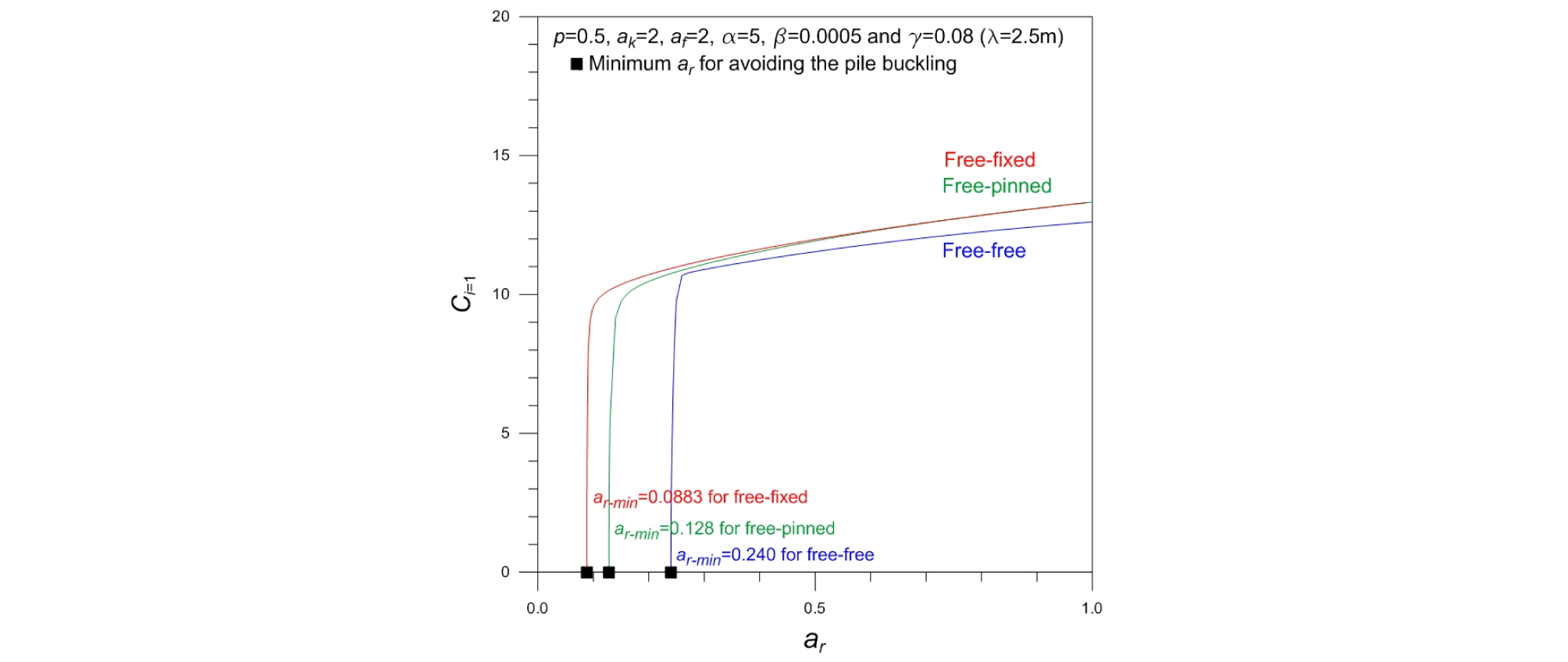
Fig. 3은 깊이 방향으로 단면이 작아지는 테이퍼 말뚝의 기본진동수변수 Ci=1에 대한 단면비 ar의 영향을 나타낸다. 원형통 말뚝(ar=1)에서 가장 큰 Ci=1값을 갖으며 ar가 감소함에 따라 Ci=1는 감소하여 “■”로 표시한 좌표에서 Ci=1이 된다. 이는 말뚝선단의 단면비가 임계값(critical value) 이하로 작아지면 정적 수평거동이 동적 자유진동보다 우세하여 말뚝이 좌굴되기 때문이다. 한 예로서 자유-자유의 단부조건에서 주어진 수직하중변수 p=0.5에 대한 임계 단면비 ar=0.240에서 테이퍼 말뚝은 좌굴되며, 이는 해당 말뚝의 좌굴하중변수가 b=0.5임을 의미한다.
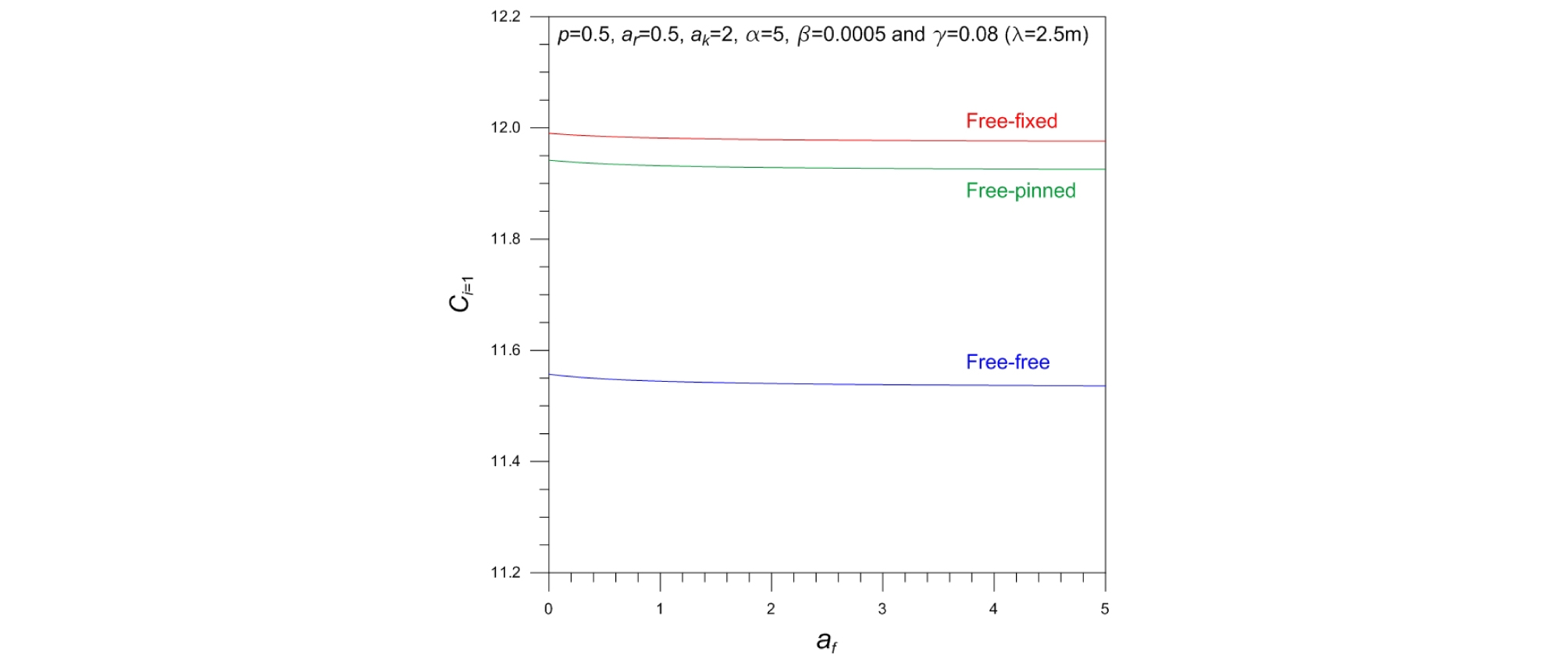
Fig. 4는 테이퍼 말뚝의 기본진동수변수 Ci=1에 대한 주면마찰력비 af의 영향을 나타낸다. 여기서 주면마찰력비는 0 < af < 5의 값을 가지며 af=1은 깊이 방향으로 주면마찰력이 일정한 경우이다. 말뚝의 단부조건에 상관없이 af가 증가하면 Ci=1는 감소하며 af의 영향성은 af가 작을수록 큰 것을 확인할 수 있다.
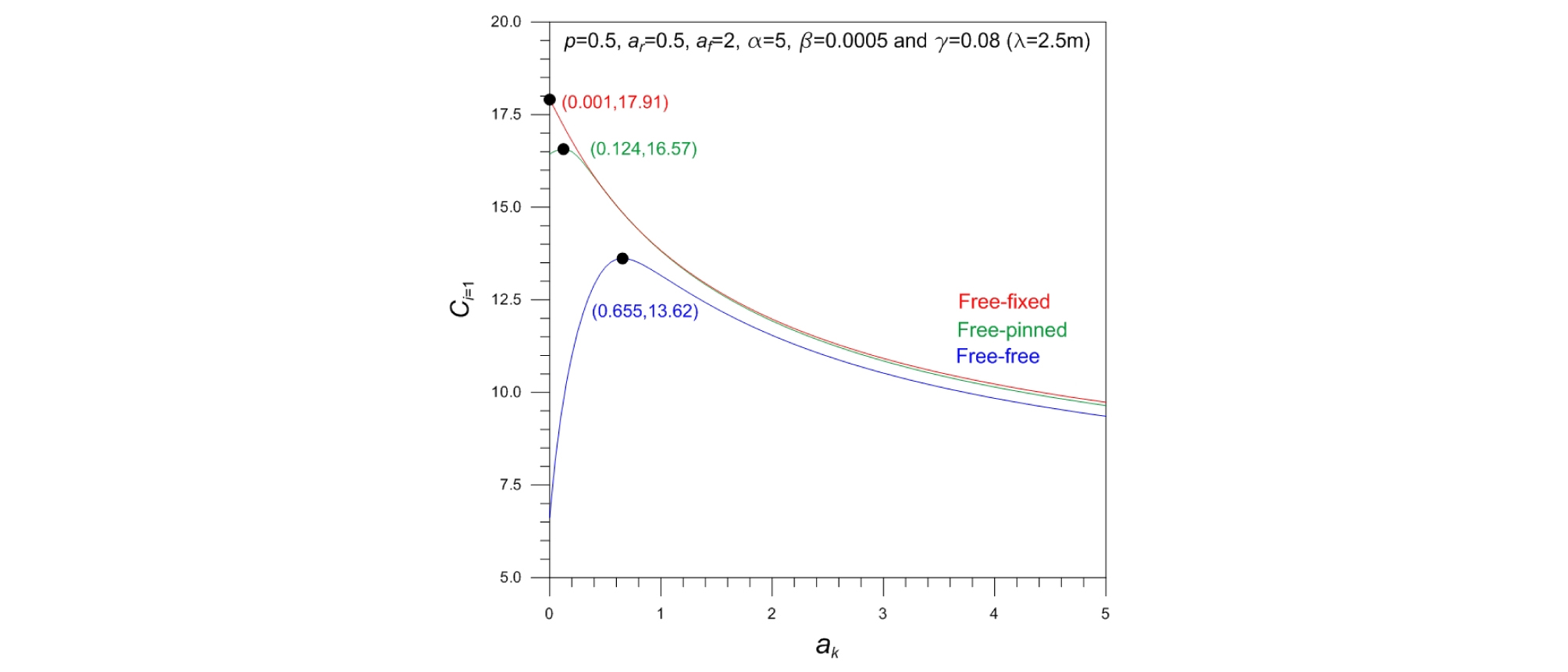
Fig. 5는 테이퍼 말뚝의 기본진동수변수 Ci=1에 대한 지반계수비 ak의 영향을 나타낸다. 여기서 ak < 1는 지반반력이 깊이에 따라 작아지는 경우이며 ak > 1는 그 반대의 경우이다. ak=1인 균질지반을 경계로 하여 ak < 1에서 지반반력이 자유진동에 미치는 영향성이 ak > 1에 비해 크다. 또한, Ci=1에 대한 ak의 영향성은 말뚝의 단부조건에 의존하는 것을 확인할 수 있다. 예로서 자유-회전 말뚝의 경우 ak가 증가하면 Ci=1은 증가하다가 “●”로 표시한 좌표에서 최대치를 보인 후 감소한다. 이는 주어진 말뚝조건에서 가장 큰 Ci=1을 갖는 지반계수비 ak가 존재함을 의미한다.
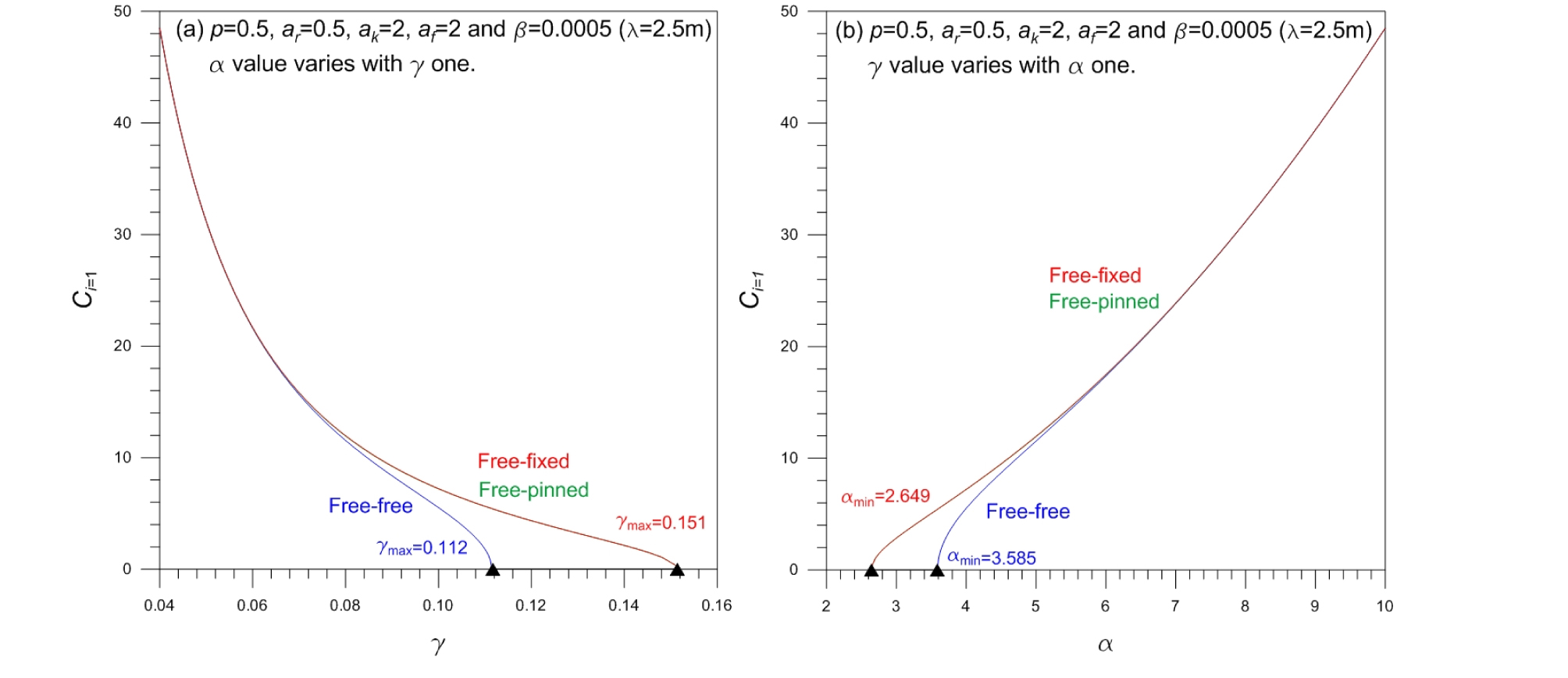
Fig. 6은 테이퍼 말뚝의 기본진동수변수 Ci=1에 대한 직경비 γ와 특성길이비 α의 영향을 나타낸다. 앞서 설명한 바와 같이, γ와 α는 상호 종속적인 관계에 있으므로 Fig. 6에 Ci=1에 대한 γ와 α의 관계를 함께 도시하였다. γ의 증가는 α의 감소를 의미하며 이 경우 Ci=1은 감소한다. Fig. 3과 유사하게 Fig. 6에서도 Ci=1=0인 γ와 α가 존재(“▲”로 표시)한다. 한 예로 자유-고정 조건에서 γ=0.151, α=2.649(즉, γα=0.4)를 갖는 말뚝의 좌굴하중변수는 b(=p)=0.5이다. Prakash and Sharma(1990)에 따르면 α > 2인 말뚝은 연성말뚝(flexible pile)으로 평가되며 이로부터 주어진 수치예는 연성말뚝의 자유진동 특성을 나타낸다.
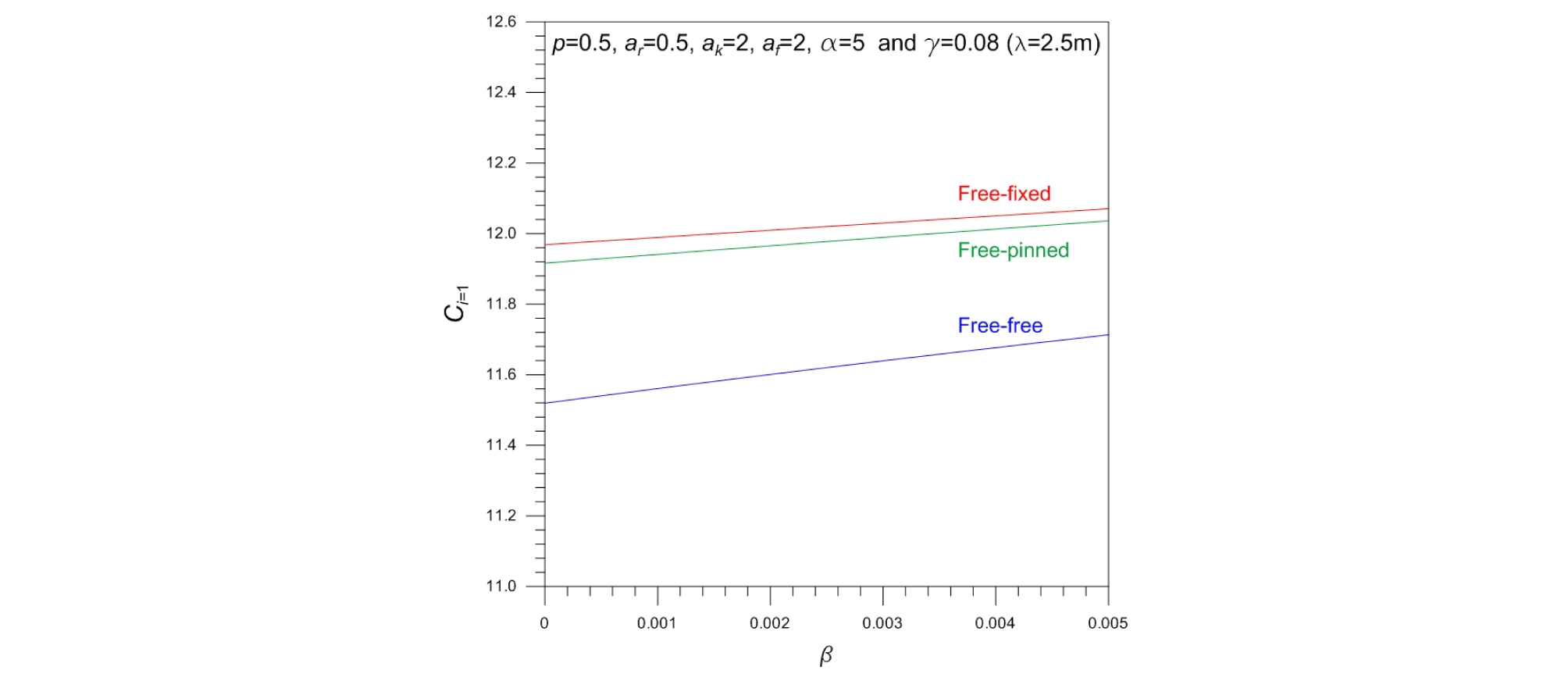
Fig. 7은 테이퍼 말뚝의 기본진동수변수 Ci=1에 대한 주면마찰변수 β의 영향을 나타낸다. β가 증가하면 Ci=1는 거의 선형적으로 증가하나, β에 따른 Ci=1의 변화율은 자유-자유조건이 가장 큰 것을 확인할 수 있다. 이는 일정한 수직압축하중 하에서 테이퍼 말뚝의 주면마찰력이 크고 말뚝단부의 구속 정도가 작을수록 고유진동수가 크다는 것을 의미한다.
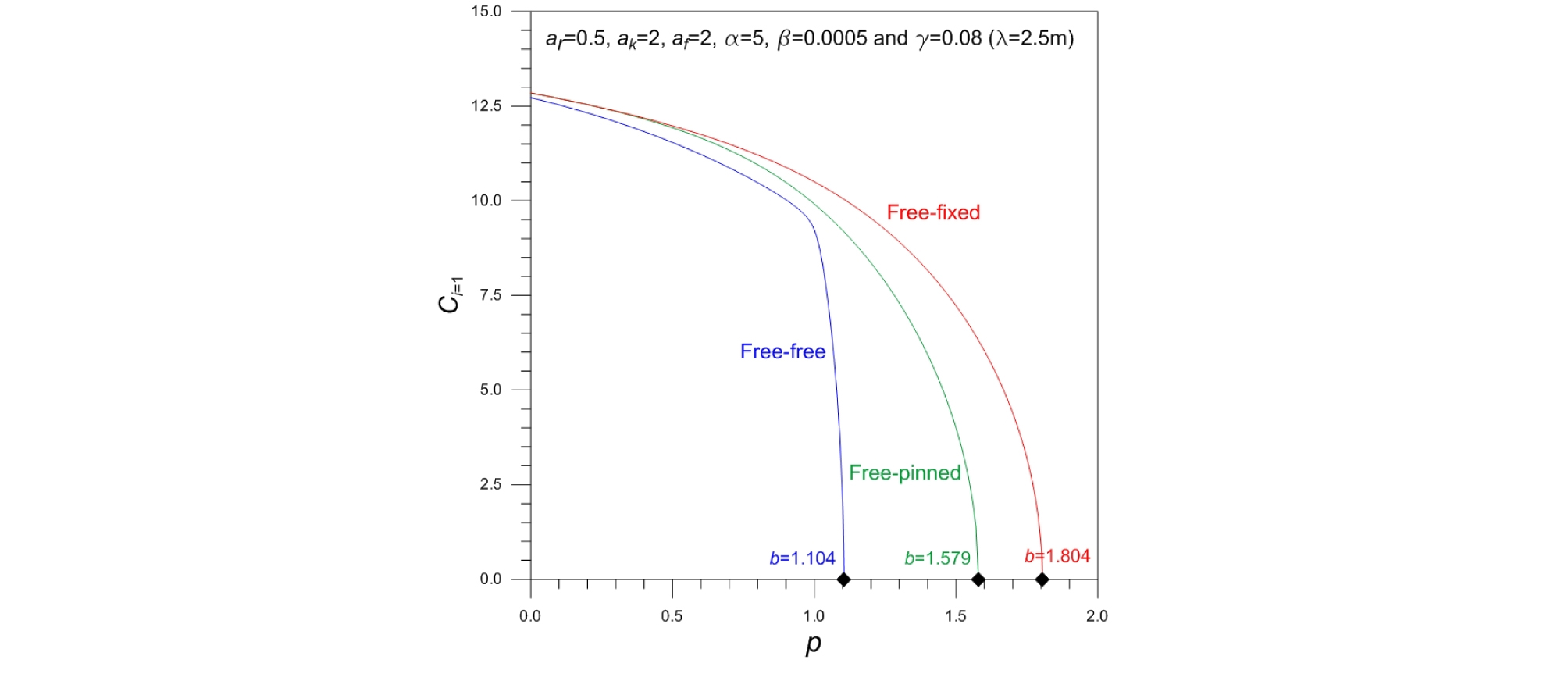
Fig. 8은 테이퍼 말뚝의 기본진동수변수 Ci=1에 대한 수직하중변수 p의 영향을 나타낸다. p가 증가할수록 Ci=1은 감소하고 그 감소율은 증가하여 “◆”로 표시한 p에서 Ci=1=0이 된다. 이는 수직압축하중이 좌굴하중에 도달하면 말뚝은 수평방향 굽힘으로 인해 좌굴하여(Bhattacharya et al., 2009) 말뚝은 정적 상태, 즉 Ci=1=0이 되기 때문이다. 예로서 자유-자유 조건에서 테이퍼 말뚝은 수직하중변수 p=1.104에서 Ci=1=0이 되며, 이는 테이퍼 말뚝의 좌줄하중변수가 p=1.104임을 의미한다.
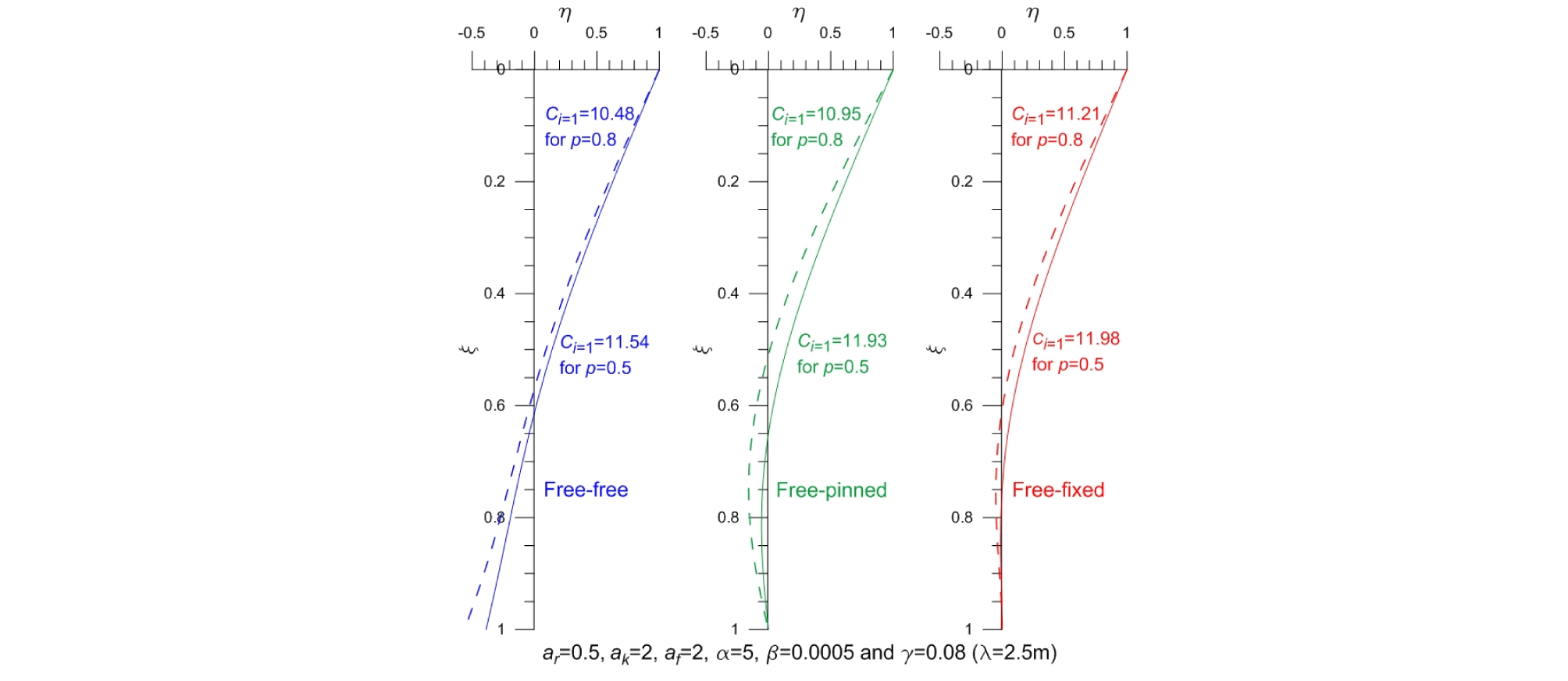
Fig. 9는 수직하중변수 p=0.5와 p=0.8인 테이퍼 말뚝의 모드형상을 보여준다. 모드형상은 수직하중변수에 따라 그 형태는 크게 변화하지 않으나 그 동적변위는 수직하중변수가 클수록 큰 것을 확인할 수 있다. 또한, 모드형상은 단부조건에 의존하여 말뚝선단이 자유조건인 경우 동적변위가 발생하고 회전과 고정인 경우 동적변위가 발생하지 않는다.
5. 결 론
본 연구에서는 정적 수직하중을 받는 테이퍼 마찰말뚝의 자유진동 특성을 평가할 수 있는 해석모델을 제안하였다. 제안한 해석모델의 검증을 위하여 원통형 말뚝에 대한 기존 문헌과 해석모델의 고유진동수를 비교한 결과, 두 값은 잘 일치하였다. 수치해석 결과로부터 다음과 같은 결론을 도출하였다. 말뚝의 단면비 ar가 감소할수록 Ci=1는 감소한다. ar에 따른 Ci=1 변화를 분석하면 말뚝의 좌굴이 발생하는 임계 단면비를 결정할 수 있다. 기본진동수변수 Ci=1는 말뚝의 주면마찰력비 af가 증가할수록 감소하나, 주면마찰변수 β가 증가할수록 증가한다. 지반반력이 깊이에 따라 작아지는 경우, 즉 지반계수비 ak < 1에서 자유진동에 대한 지반반력의 영향성이 반대의 경우(ak > 1)에 비해 크다. 직경비 γ와 특성길이비 α는 상호 종속적인 관계이며 γ가 증가하면 Ci=1는 감소하고, α가 증가하면 Ci=1는 증가한다. 수직하중변수 p가 증가할수록 Ci=1은 감소하고, 좌굴하중변수 b(=p)에서 말뚝은 좌굴되고 Ci=1=0이 된다. 이와 같이 제안된 해석모델은 말뚝의 변단면, 주면마찰력, 단부조건, 수직압축하중 및 지반의 불균질성이 반영된 말뚝의 고유진동수와 진동형상을 산정할 수 있으며, 이는 지진과 같은 동적하중을 받는 말뚝의 설계에 활용될 수 있다.