1. 서 론
2. 이론적 고찰
2.1 수평지반반력계수 산정법
2.2 말뚝의 수평지지력 산정
2.3 p-y곡선의 특성
3. 비선형해석
3.1 해석조건
3.2 비선형 해석결과
4. 수평거동특성 평가
4.1 수평지지력 평가
4.2 수평변위 평가
4.3 휨모멘트 평가
4.4 케이싱 보강조건의 효율성 평가
5. 결 론
1. 서 론
최근 대형 구조물 및 교량의 건설이 활발해짐으로 인해 큰 하중을 지지하기 위한 대구경 현장타설말뚝의 시공이 증가하고 있다. 대구경 현장타설말뚝은 말뚝 한 본당 차지하는 하중분담률이 상대적으로 크기 때문에 지지력이 부족할 경우 구조물에 큰 피해를 일으킬 수 있다. 이러한 대구경 현장타설말뚝의 지지력은 소구경 말뚝보다 크기 때문에 시공시 소요개수가 적으며, 큰 수평하중이나 휨모멘트에 저항할 수 있다. 또한 조밀한 모래나 자갈층에서 대구경 현장타설말뚝을 설치하는 것이 용이하며, 소음 및 진동, 지반융기나 인접말뚝의 변형 등과 같은 문제가 발생하지 않아 시공성이 좋은 장점을 가지고 있다. 그러나 시공 후의 품질검사가 어려우며, 시공을 위한 깊은 굴착이 지반 침하 및 인접구조물의 피해를 유발시킬 수 있는 단점을 가지며 이러한 단점을 해결하기 위해 현장타설말뚝 공법인 파일벤트(Pile Bent) 구조물이 제시되었다. 말뚝과 기둥이 일체화된 파일벤트 구조물의 경우 말뚝과 기둥의 경계부가 모호하지만 최근 지표면을 기준으로 지표면 아래는 말뚝체, 지표면 위로는 기둥부로 구분하자는 의견이 제시되었다. 이러한 의견에 따르면 파일벤트 구조물의 경우 대구경 철근 콘크리트말뚝을 사용하기 때문에 지표면 아래의 말뚝체는 대구경 현장타설말뚝과 동일하다 판단할 수 있다.
파일벤트 구조물의 구조적 특성은 수직하중에 대한 저항성이 크지만 교각기둥과 코핑에 작용하는 수평하중에는 상대적으로 취약하다는 단점이 존재한다. 따라서 이러한 단점을 보완하기 위한 수평저항력을 확보하는 방법은 말뚝 자체의 강성을 증가시키는 방법과 말뚝 주변지반의 강성을 증가시키는 방법이 있으며 최근 두 방법 중에서 말뚝체의 강성을 증가시키는 방법을 많이 사용하는 추세이며 올케이싱(All Casing)공법이 이에 해당한다. 그러나 케이싱 보강공법은 보강길이가 늘어남에 따라 강성이 증가하지만 공비 또한 점차적으로 증가하기 때문에 All Casing공법을 적용하기보다는 지반조건별로 적정 케이싱 보강길이를 판단하여 적용한다면 공사기간과 공사비를 감축시킬 수 있을 것으로 판단된다.
말뚝의 수평거동은 말뚝의 직경과 재료에 따른 강성조건과 인접지반의 강성에 관련된 수평지반반력계수(kh)에 큰 영향을 받는다. 이 계수는 기존 연구자들(Bowles, 1988; Chen, 1978; Hukuoka, 1966; KGS, 2015; Vesic, 1961 등)의 경험식을 통해 산정할 수 있다. 또한 이 경험식을 통해 대구경 현장타설말뚝에 대한 수평거동특성을 평가하는 연구가 최근 진행되었다(Yang, 2020). 또한 현장타설말뚝의 지지력특성에 관한 실험적 연구를 통해 중구경 현장타설말뚝의 말뚝의 강도에 따른 지지력을 비교분석하였으며 수평하중을 받는 말뚝의 수평거동은 p-y곡선을 이용한 비선형해석으로 국내에서 많이 수행되어 왔으며(Baek, 1998; Ryu, 2003 등) p-y곡선은 기존 연구진들에 의해 지반조건에 따라 연구되어 왔다(Matlock, 1970; Reese et al., 1974 등). 이와 같이 p-y곡선을 통한 파일벤트 구조물의 수평거동특성 또한 기존에 연구되었다(Jeong et al., 2006).
따라서 본 연구에서는 말뚝의 수평저항력을 확보하기 위해 말뚝체의 강성을 증가시키는 케이싱 보강공법에 대하여 연구하였으며 지반조건에 따라 효과적인 케이싱 보강길이를 판단하기 위해 지반조건은 현장실무에서 많이 사용하는 SPT의 N치(5, 25, 45)를 사용하였다. 또한 수치해석시 적용할 케이싱 보강길이는 기존 연구(Yang, 2020)에서 제안한 케이싱 길이상수(κ=0.4, 1.2, 2.0)를 적용하여 각 지반 및 케이싱 보강길이 조건에 따라 어느 정도의 수평지지력을 확보하는 것이 가능한지 분석하기 위해 비선형해석프로그램인 L-Pile을 이용하여 p-y곡선해석을 수행하였으며 수치해석 된 결과를 이용하여 말뚝의 수평거동특성을 비교 분석하여 적정 케이싱 보강길이를 제안하였다.
2. 이론적 고찰
2.1 수평지반반력계수 산정법
본 연구에서 비선형 해석(L-PILE 프로그램)을 수행하는 경우 수평지반반력계수(kh)가 요구되며 이 계수는 말뚝체의 휨거동 특성 인자인 1/β 산정에도 주요 고려 인자임과 동시에 대구경 현장타설의 수평지지력 산정시에도 중요한 인자이다. 수평지반반력계수의 산정은 Bowles(1988), Chen(1978), Hukuoka(1966), Vesic(1961) 그리고 상시와 지진시의 KGS(2015) 경험식을 바탕으로 산정하는 것이 일반적이며, 각각의 산정방법은 Table 1에 나타내었다.
Table 1.
Estimate method of horizontal subgrade reaction coefficient, kh (Yang et al., 2020)
| Proposer | Equation |
| Bowles (1988) | |
| Chen (1978) | where, C=3.0 (sand) ; C=1.6 (clay) |
| Hukuoka (1966) | |
| KGS (2015) | where, α=1.0(Normal condition) ; α=2.0(Earthquake condition) |
| Vesic (1961) |
여기서, Es : 지반의 탄성계수, D : 말뚝의 직경 , N : SPT, N치, EpIp : 말뚝의 휨강성, μ : 지반의 포아송비
2.2 말뚝의 수평지지력 산정
말뚝의 수평지지력을 산정하는 방법은 대표적으로 Broms(1964)가 제시한 극한평형법이 있으며 이 방법은 Table 2에 나타낸 것처럼 지반을 점성토와 사질토로 구분하여 말뚝의 극한수평지지력을 평가하는 방법을 제시하였다. 말뚝의 구분은 짧고 단단하거나 길고 유연한 말뚝으로 분류하였으며 말뚝머리의 조건도 자유와 고정으로 구분하였다. 따라서 파괴형태가 짧고 단단한 말뚝의 경우에는 주변 지반의 파괴로 인한 말뚝의 회전거동에 의해 파괴되는 것으로 간주하였으며 길고 유연한 말뚝의 경우 최대휨모멘트가 말뚝의 휨강성을 초과했을 때 파괴되는 것으로 가정하여 지표면 아래 일정깊이에서 소성힌지가 형성되었다고 판단하였다.
Table 2.
Classification of pile condition (Yang et al., 2020)
| Pile condition | Clay | Sand | Remarks |
| Short pile | βL ≤ 2.25 | ηL < 2.0 | and |
| Medium Pile | - | 2.0 ≤ ηL ≤ 4.0 | |
| Long Pile | βL > 2.25 | ηL > 4.0 |
2.3 p-y곡선의 특성
p-y곡선은 일반적으로 수평하중이 재하 된 말뚝의 거동을 해석하는 방법이며 p는 수평지반반력을 뜻하며 y는 말뚝의 변위를 뜻한다. 따라서 말뚝에 수평하중이 재하되는 경우 말뚝의 변위가 커짐으로 인해 지반의 반력이 항복치에 도달하는 관계를 나타내는 곡선이다.
p-y곡선으로 분석하는 경우 휨에 관련된 말뚝의 물리적 거동은 휨강성으로 나타내며 일반적으로 수평하중을 받는 말뚝의 거동을 설명하기 위해 말뚝 자체가 선형 및 탄성구조를 가진다는 가정에 기초한다.
| $$EI\frac{d^4y}{dx^4}+k_hy=0$$ | (1) |
여기서, EI는 말뚝의 휨강성을 의미하며 x는 특정위치의 말뚝길이, y는 말뚝의 수평변위를 의미한다. 이를 통해 말뚝의 수평 거동은 말뚝의 휨강성 및 수평지반반력계수와 큰 상관관계를 가진다는 것을 알 수 있다.
3. 비선형해석
본 연구는 대구경 현장타설말뚝의 수평지지력을 증가시키기 위해 말뚝체에 케이싱을 보강할 경우 그 보강길이에 따른 보강효과를 평가하는데 목적이 있다. 따라서 이를 위해 지반조건인 SPT의 N치를 적용하고 실무에서 사용성이 높은 비선형해석 프로그램인 L-Pile 프로그램을 활용하여 케이싱 보강길이별 수평거동특성을 연구하였다.
3.1 해석조건
3.1.1 모델링 및 지반해석
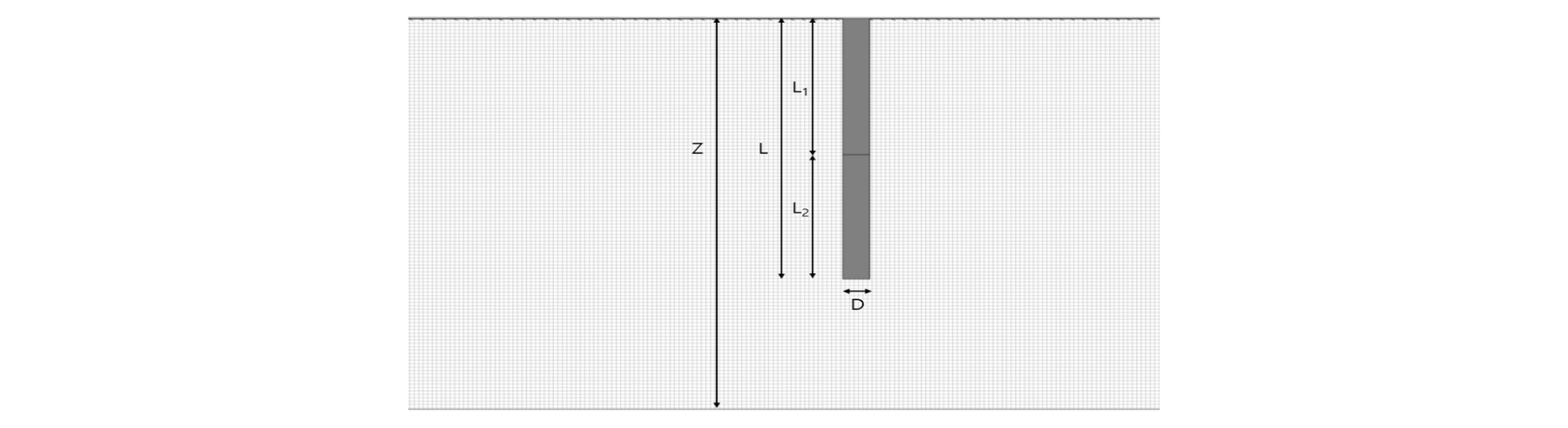
Fig. 1은 본 연구에서 활용한 L-Pile 프로그램의 모델링을 나타낸 것으로 L1은 말뚝의 케이싱 보강길이를 뜻하며, L2는 케이싱 보강을 하지 않은 콘크리트 말뚝을 뜻한다. 그리고 L은 말뚝의 전체길이를 뜻하며 D는 말뚝의 직경, Z는 지반의 깊이를 의미한다. 지반의 깊이는 비선형해석모델에서는 말뚝의 구속조건을 무시하지만 유한요소해석의 경우 바닥부의 구속조건에 따라 해석결과에 차이가 있을 것으로 판단되기 때문에 이를 고려하여 말뚝길이의 1.5배로 적용하였다.
본 연구에서는 모래지반에서 적용 가능한 p-y곡선인 Reese et al.(1974)의 Sand모델을 사용하였으며 이 모델은 기본적으로 해석절차가 간편하고 수평하중을 받는 말뚝의 수평거동분석에 일반적으로 사용되는 모델이다. 수치해석시 해당 모델에 필요한 지반해석조건을 산출하기 위해 지반조건은 실무적으로 많이 활용되는 SPT의 N치를 이용하였으며 N치는 Table 3과 같이 5, 25, 45를 선택하여 각각 느슨함, 보통, 조밀한 특성에 대해 나타내도록 설정하였다. 여기서 적용된 N치에 따른 흙의 단위중량(γ')과 내부마찰각()은 한국지반공학회(KGS)에서 제안한 값을 고려하였다.
말뚝의 수평거동을 분석하는데 중요한 수평지반반력계수의 결정은 기존에 연구된 Yang(2020)의 연구에서 대구경 현장타설말뚝을 대상으로한 수평지반반력계수는 Vesic(1961)의 제안식을 적용하는 것이 타당하다고 제안하였기 때문에 Vesic(1961)의 제안식을 적용하였으며 제안식에 필요한 지반의 탄성계수는 NAVFAC DM-7(1986)에서 제안한 공식인 700N을 적용하였으며 이를 지반 물성치인 N치에 따라 산출하여 수평지반반력계수를 적용하였다.
위에서 언급한 지반의 수치해석모델링을 토대로 지반의 해석조건 및 물성치를 정리하면 Table 3과 같다.
Table 3.
Soil condition of numerical analysis
| Material | SPT-N | Soil Density | γ' (kN/m3) | (°) | Kh (kN/m3) | Depth (m) |
| Sand | 5 | Loose | 16.0 | 25° | 1,244 | L*1.5 |
| 25 | Medium | 17.0 | 30° | 6,410 | L*1.5 | |
| 45 | Dense | 18.0 | 33° | 11,966 | L*1.5 |
3.1.2 말뚝 및 케이싱 해석조건
비선형해석 시 말뚝의 재료는 가장 많이 활용되는 콘크리트를 적용하였으며 케이싱 보강재료는 강관으로 적용하였다. 해석조건으로 말뚝의 직경은 대구경 현장타설말뚝의 경우 장비특성상 직경이 3m를 초과할 경우 시공성이 저하되며 경제성도 낮은 것으로 확인되어 실무적으로 사용 가능한 가장 큰 단면인 3m를 적용하였다. 말뚝의 총 길이의 경우 휨거동 영향 범위인 1/β과 케이싱 보강길이를 고려하여 2·(1/β)에 말뚝의 하부 구속력에 따른 차이를 줄이기 위해 여유길이를 5m 추가적으로 더하여 산정하였다.
유한요소해석은 말뚝재료의 해석조건 중 하나인 탄성계수의 경우 콘크리트말뚝의 탄성계수 및 2차단면모멘트와 케이싱 보강재료인 강관의 탄성계수 및 2차단면모멘트를 적용하면 프로그램 상 산출을 해주지만 비선형해석의 경우 직접 계산하여 케이싱 보강된 콘크리트말뚝의 탄성계수를 산출해야 한다. 따라서 본 연구에서 모델링 한 케이싱 보강 말뚝의 경우 케이싱 보강두께는 30mm를 적용하였으며 이를 토대로 탄성계수를 계산하여 적용하였다. 결론적으로 말뚝 및 케이싱 재료의 비선형 해석조건은 Table 4에 나타내었다.
Table 4.
Pile and casing condition of numerical analysis
본 연구의 목적인 케이싱 보강길이에 따른 말뚝의 수평지지특성의 보강효과를 판단하기 위한 핵심 조건인 케이싱 보강길이는 Yang(2020)의 연구에서 제안한 케이싱 보강 길이비(κ)를 이용하였으며 해당 길이비와 휨거동 영향 범위를 통해 케이싱 보강길이를 적용하였다.
| $$케\mathrm 이\mathrm 싱\;\mathrm{보강}\;\mathrm{길이비}(\mathrm{Reinforced}\;\mathrm{Length}\;\mathrm{Ratio},\;\mathrm\kappa)=l/(1/\beta)$$ | (2) |
여기서, l는 케이싱 보강길이(m)를 나타내며 휨거동 영향범위인 1/β(m)은 Table 2에 나타낸 것처럼 산정할 수 있다. 따라서 본 연구에서 적용한 수치해석 조건은 Table 5과 같이 케이싱 보강길이를 무보강 조건(Non Reinforced), κ=0.4, 1.2, 2.0, All Casing 조건에 따라 산출하여 적용하였다.
Table 5.
Pile and casing condition of numerical analysis
| SPT-N | Reinforced Length Ratio (κ) | Casing Reinforced Length (m) |
| 5 | 0.4 | 6.8 |
| 1.2 | 20.4 | |
| 2.0 | 34 | |
| All Casing | 39 | |
| 25 | 0.4 | 4.8 |
| 1.2 | 14.4 | |
| 2.0 | 24 | |
| All Casing | 29 | |
| 45 | 0.4 | 4 |
| 1.2 | 12 | |
| 2.0 | 20 | |
| All Casing | 25 |
3.1.3 수평하중 해석조건
본 연구에서 진행한 비선형 해석시 말뚝에 작용하는 하중조건은 정적하중조건을 적용하였으며 대구경 현장타설말뚝의 경우 일반적으로 수직하중에 대해서는 지지력이 크며 본 연구에서는 수평 하중이 재하된 대구경 현장타설말뚝의 수평거동특성을 알아보기 위해 수직하중과 모멘트하중은 적용하지 않고 수평하중만 적용하였다.
말뚝의 수평지지력의 경우 KR(2012), KGS(2015) 등의 관련기관별로 제시된 말뚝의 허용수평변위는 직경이 1,500mm 이하인 경우 말뚝의 허용변위는 15mm 이하를 적용하며, 직경이 1,500mm 이상인 경우 말뚝의 허용변위를 직경의 1% 이하에 해당하는 수평변위를 적용하기 때문에 현장타설말뚝직경의 1%에 해당하는 변위를 나타내는 수평하중을 Fig. 2와 같이 반복해석하여 산출한 후 적용하였다. 지반조건에 따른 케이싱 보강 길이별 수평하중 해석조건은 Table 6에 나타내었다.
Table 6.
Lateral load value of numerical analysis
| Pile | SPT-N | Lateral Load (kN) |
| Non Reinforced | 5 | 1,390 |
| 25 | 3,720 | |
| 45 | 5,410 |
3.2 비선형 해석결과
3.2.1 수평지지력
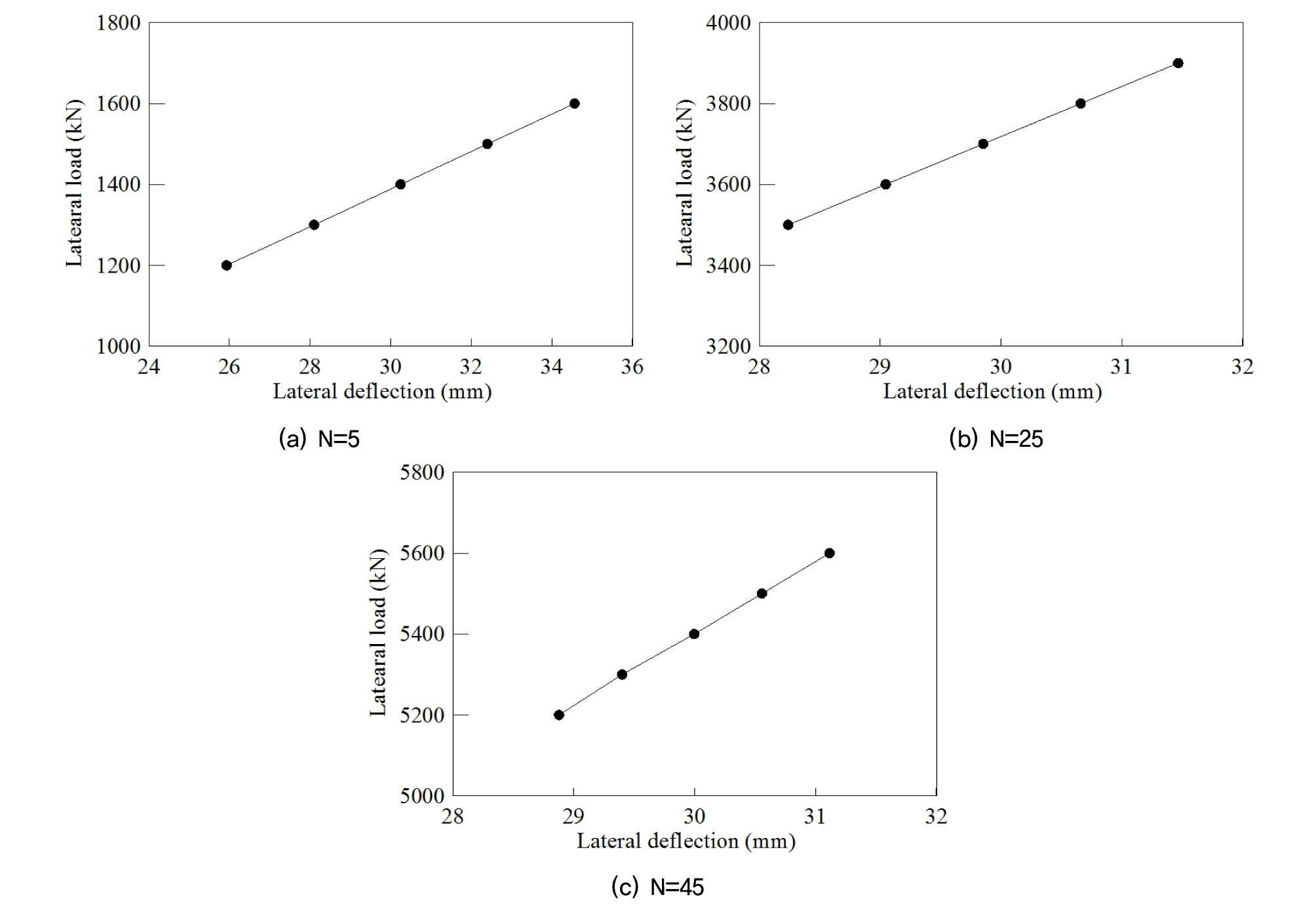
Fig. 3은 비선형해석을 이용하여 케이싱 보강길이별로 말뚝의 수평지지력을 나타낸 것으로 본 연구에서 말뚝의 직경을 3,000mm로 적용하여 말뚝의 변위가 30mm에 해당하는 수평하중을 말뚝의 수평지지력으로 판단하였으며 말뚝의 수평지지력은 SPT의 N치의 크기와 상관없이 케이싱 보강조건에 비례하여 증가하는 것을 알 수 있다.
3.2.2 수평변위 및 휨모멘트
Fig. 4는 수평하중조건을 적용할 경우 수평변위의 해석결과를 나타낸 것이다. 수평변위의 경우 무보강 조건은 허용수평변위인 30mm를 만족하였으며 케이싱의 보강길이가 늘어남에 따라 수평변위는 점차적으로 감소하는 경향을 나타냈다. 또한 케이싱의 보강조건과 관계없이 휨거동이 발생되는 것으로 예측되었다.
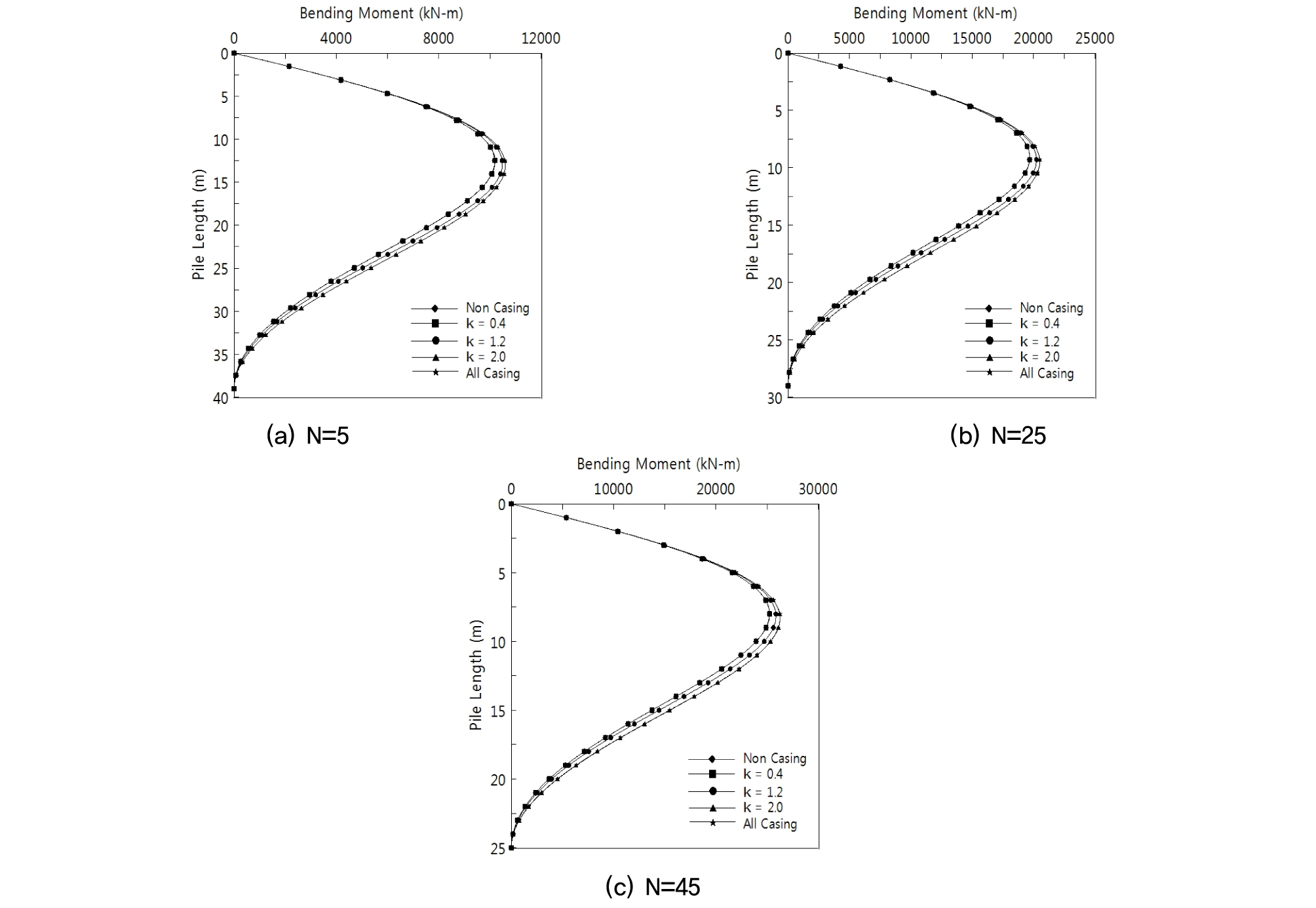
Fig. 5는 말뚝체에 발생한 모멘트 결과를 나타낸 것이며 지반이 조밀할수록 또는 케이싱 보강길이가 증가함에 따라 더 큰 휨모멘트를 받는 것으로 나타났다. 최대휨모멘트의 위치는 지반별 말뚝 길이의 약 30%에 위치한 것으로 확인되었다.
4. 수평거동특성 평가
4.1 수평지지력 평가
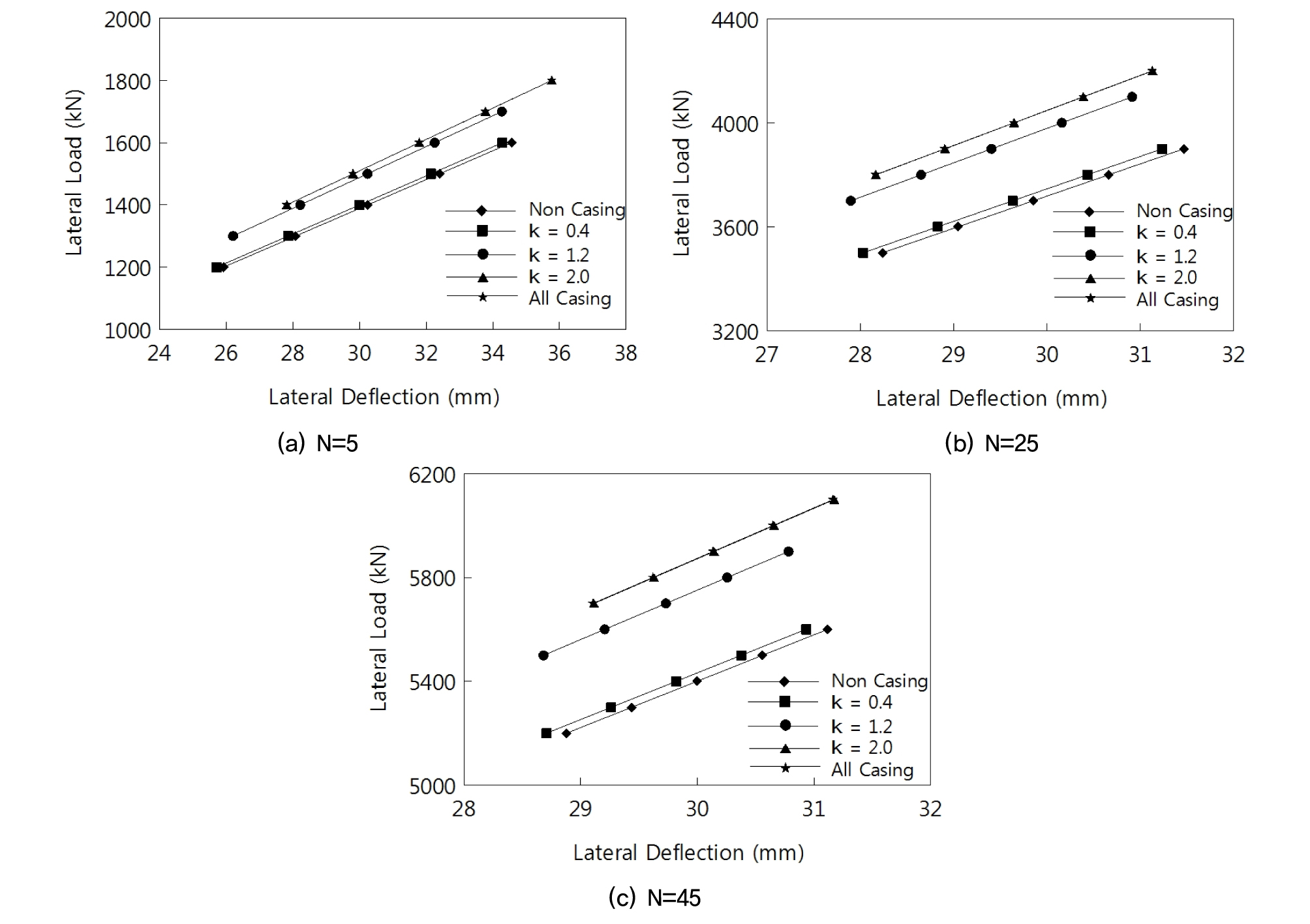
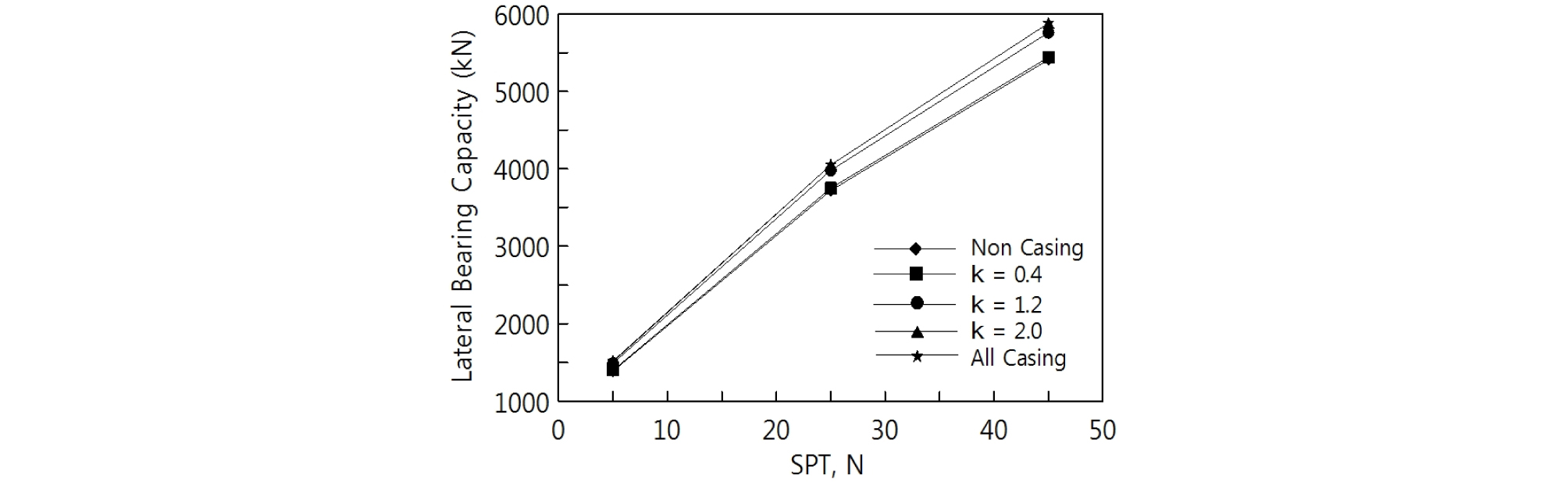
Fig. 6은 KR(2012), KGS(2015) 등에서 제시한 말뚝직경의 1%인 허용변위를 만족하는 수평하중을 대구경 현장타설말뚝의 수평지지력으로 판단하였으며 이를 케이싱 보강길이에 따라 비교하여 나타낸 그림이다. 이를 분석하면 지반조건에 따라 말뚝의 수평지지력이 큰 차이를 나타낸다. 이러한 결과는 지반조건인 N치에 비례하여 수평지반반력계수는 증가하며 이 수평지반반력계수는 말뚝의 수평지지력에 큰 영향을 준다는 것을 알 수 있다.
또한 케이싱 보강길이에 비례하여 말뚝의 수평지지력은 점차 증가하는 것을 알 수 있으며 케이싱보강길이에 의한 수평지지력의 보강효과는 약 9%의 증대효과를 나타내었다. 그러나 무보강조건에서 κ=0.4조건의 수평지지력의 차이는 크게 나타나지 않으며 κ=1.2조건부터 All Casing조건까지도 큰 보강효과를 나타내지 않았다. 그러나 κ=0.4조건에서 κ=1.2조건의 구간은 다른 구간에 비해 상대적으로 큰 수평지지력의 차이를 보였다.
4.2 수평변위 평가
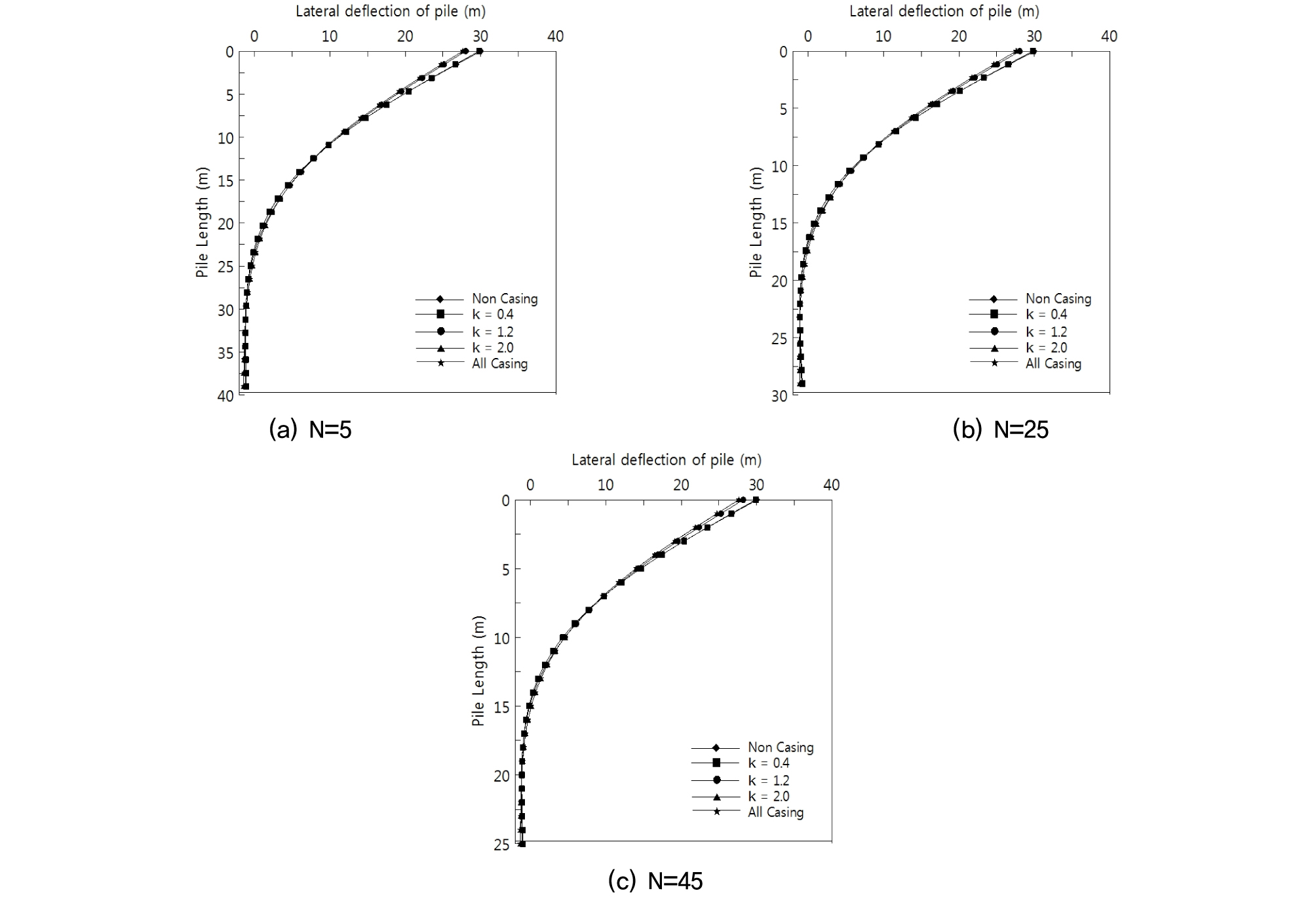
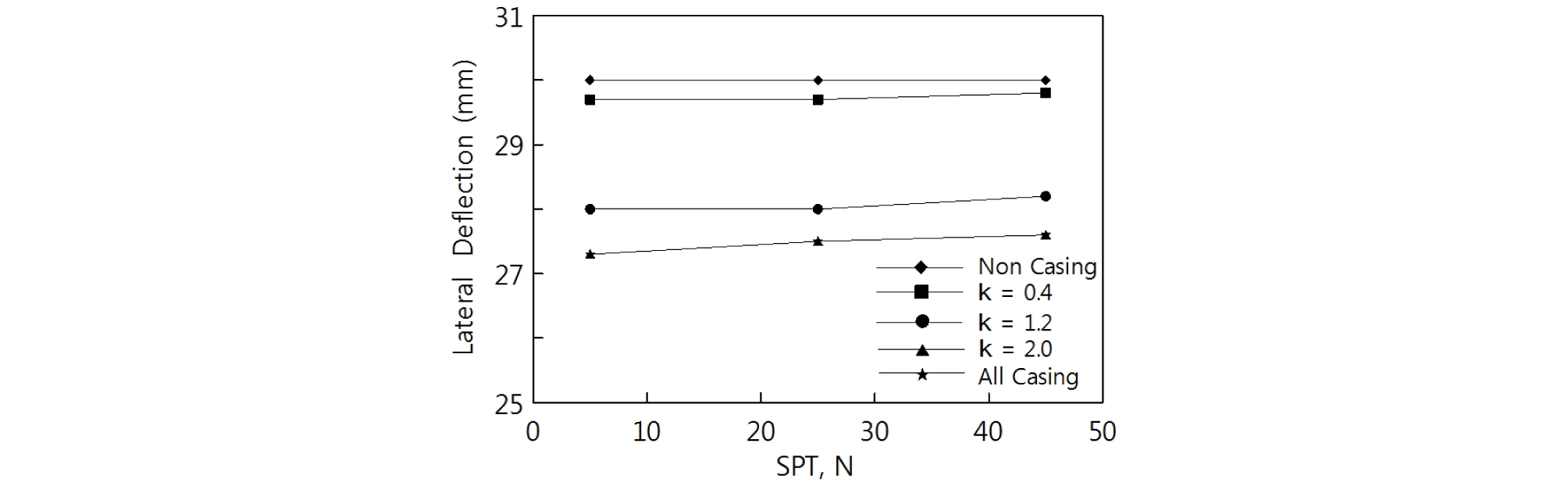
Fig. 7은 비선형해석을 통해 조사된 케이싱 보강길이별 대구경 현장타설말뚝의 수평변위를 비교한 것이다. 이를 보면 지반조건인 N치에 따라 무보강조건과 All Casing을 비교하였을 때 N치는 5일 때 말뚝의 수평변위는 약 2.7mm 감소한 것으로 나타나며 N치가 25인 경우 2.5mm, N치가 45인 경우 2.4mm가 감소한 것으로 나타났다. 이러한 결과는 지반조건이 느슨함에 따라 보강효과가 더 뛰어나다는 것을 나타낸다.
또한 케이싱 보강길이에 따라 말뚝의 강성이 증가하기 때문에 점차적으로 수평변위가 줄어드는 것을 알 수 있으며 최대 8.4%의 변위억제효과를 나타내었다. 그러나 케이싱 보강 길이비에 따라 수평변위의 감소 폭이 상이 한 것을 볼 수 있다. 무보강조건에서 κ=0.4조건의 수평변위의 변화는 약 0.3mm로 소폭 감소한 것으로 나타나지만 κ=0.4에서 κ=1.2조건의 변화는 약 1.7mm로 상대적으로 큰 감소 폭을 나타낸다. 이러한 결과는 All Casing으로 보강길이를 적용할 경우 말뚝체의 강성을 가장 많이 보강할 수 있지만 가장 효율적인 보강조건은 아님을 의미한다.
4.3 휨모멘트 평가
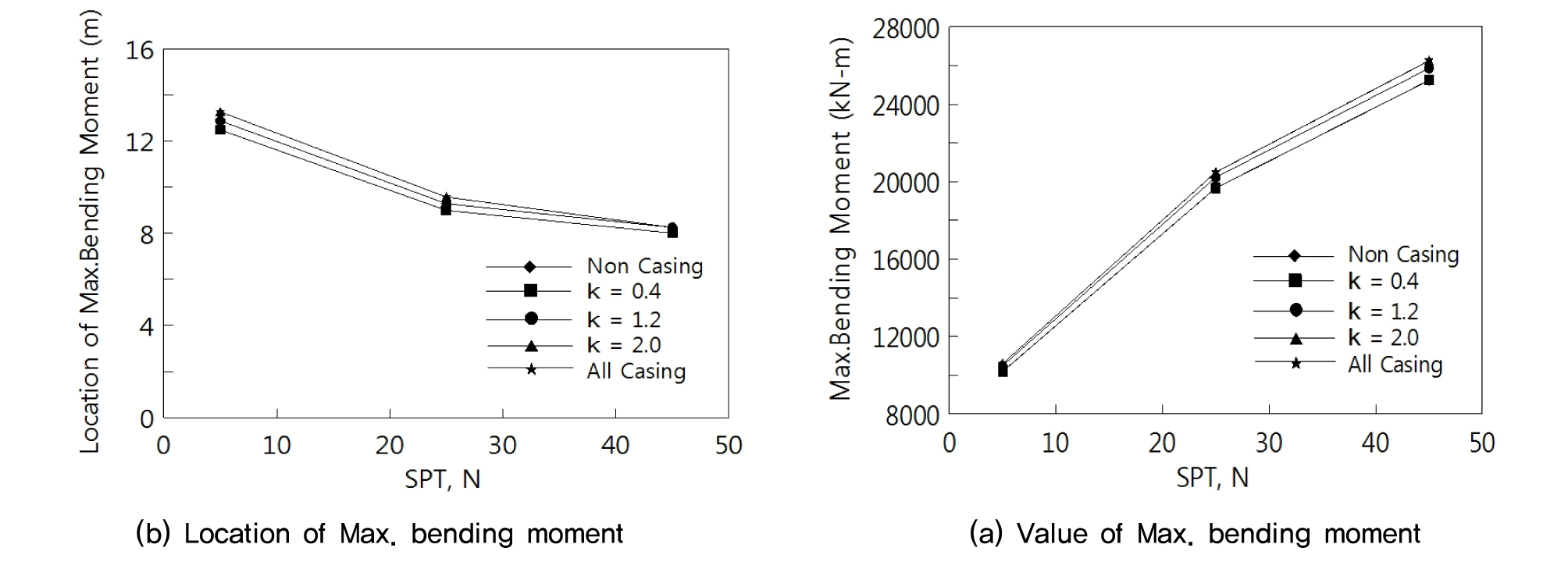
Fig. 8은 케이싱 보강길이에 따른 대구경 현장타설말뚝의 최대휨모멘트 위치와 크기를 비교하여 나타낸 것이며 Fig. 8(a)에서 나타낸 말뚝의 최대휨모멘트 위치는 지반조건에 따라 상이한 것으로 보인다. 이러한 차이는 본 연구에서 적용한 말뚝의 길이를 2・(1/β)+5m로 산정하였으며 여기서 1/β은 N치에 관련이 있어 지반조건에 따라 말뚝의 길이가 달라져서 나타난 차이로 판단된다. 따라서 객관적인 평가를 위해 각 말뚝 길이에 따라 최대휨모멘트의 위치를 비율로 환산한다면 N치가 5인 경우 지반으로부터 말뚝 길이의 약 32∼34%정도에 위치하였으며 N치가 25인 경우 31∼33%, N치가 45인 경우 32∼33%에 위치하여 지반조건과는 큰 관련이 없음을 알 수 있다. 반면에 케이싱 보강길이에 비례해서 최대휨모멘트의 위치가 깊어지는 결과를 나타내었으며 이는 최대휨모멘트의 위치는 말뚝체의 강성과 관련이 있는 것으로 판단된다.
Fig. 8(b)를 보면 케이싱 보강길이에 따라서 최대휨모멘트가 더 커지는 결과를 볼 수 있는데 최대 4%의 보강효과를 보였으며 이는 말뚝이 보강됨에 따라 분담할 수 있는 휨모멘트 크기가 커지는 것을 의미한다. 이러한 최대휨모멘트 크기의 차이를 비교분석 한 결과 다른 수평 지지특성과 마찬가지로 케이싱 보강길이에 따라 동일한 증가 폭을 나타내지 않았으며 가장 큰 증가 폭은 κ=0.4에서 κ=1.2의 구간에서 나타났으며 κ=2.0조건과 All Casing의 구간이 가장 큰 휨모멘트를 받으나 증가 폭은 가장 적은 것으로 나타났다.
4.4 케이싱 보강조건의 효율성 평가
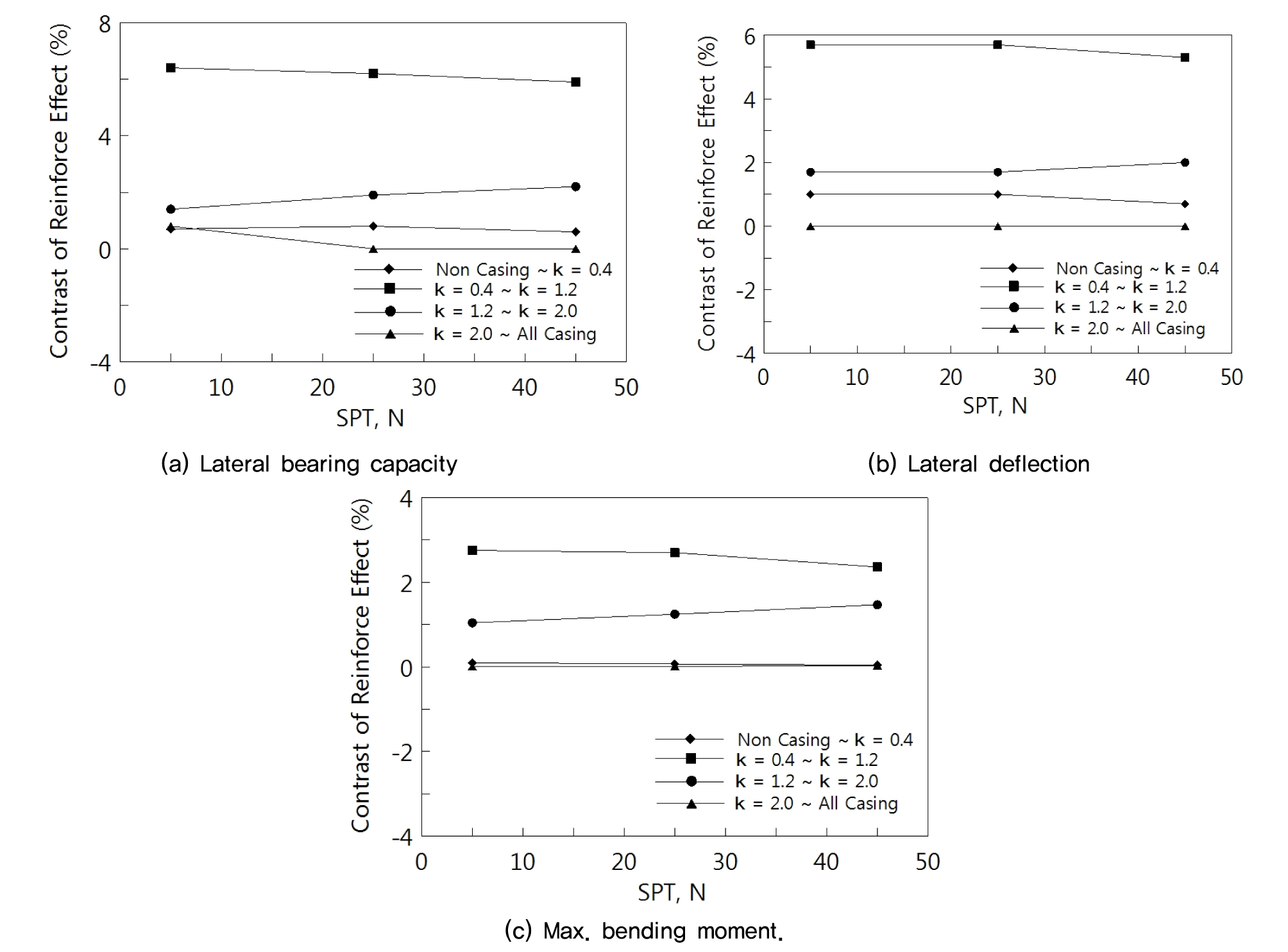
Fig. 9에 케이싱 보강조건에 따른 수평지지특성의 보강효과를 나타낸 것이며 객관적인 비교를 위해 본 연구에서 적용한 케이싱 보강조건을 구간별로 나누어서 판단하였다.
Fig. 9(a)는 수평지지력의 보강효과를 나타낸 것으로 κ=0.4에서 κ=1.2구간에서 약 6%의 가장 큰 보강효과로 나타났고 그 뒤로 κ=1.2∼2.0구간, κ=0.4∼1.2구간이 효과적인 것으로 나타났으며 κ=2.0에서 All Casing구간이 가장 작은 보강효과를 나타내었다. 따라서 본 연구에서 적용한 케이싱 보강길이 중 가장 효율적인 보강조건은 κ=1.2조건으로 나타났다.
Fig. 9(b)는 수평변위의 보강효과를 나타낸 것으로 수평지지력과 마찬가지로 κ=0.4에서 κ=1.2구간이 약 5.5%의 보강효과로 가장 크게 나타났으며 κ=2.0에서 All Casing구간이 가장 작은 보강효과를 나타내었다. 따라서 수평변위측면에서도 κ=1.2조건이 가장 효율적인 보강조건으로 나타났다.
Fig. 9(c)는 최대휨모멘트의 보강효과를 나타낸 것으로 수평지지력 및 수평변위조건과 동일한 결과를 나타내었다. 따라서 본 연구에서 진행한 케이싱 보강길이에 따른 효율성을 판단한 결과 κ=1.2조건이 지반조건과 관계없이 가장 효율적인 보강조건으로 판단된다.
5. 결 론
본 연구는 케이싱 보강길이에 따른 대구경 현장타설말뚝의 보강효과를 평가하기 위해 비선형해석을 수행하였으며 지반조건에 따른 케이싱 보강길이별 말뚝의 수평지지특성을 수치해석을 통해 비교분석한 결과로 다음과 같은 결론을 얻었다.
(1) 대구경 현장타설말뚝을 대상으로 L-Pile프로그램을 이용해 비선형해석을 수행한 결과 케이싱의 보강효과는 조밀한 지반에 비해 느슨한 지반일수록 더 효과적인 것으로 나타났으며 이는 지반이 느슨할수록 말뚝체가 더 큰 하중을 받기 때문인 것으로 판단된다.
(2) 케이싱의 보강길이에 비례하여 수평지지특성이 증가되었으며 케이싱 보강으로 인한 효과는 무보강조건에 비해 수평지지력의 경우 최대 9%의 보강효과가 나타났다. 또한 수평변위는 최대 8.4%의 변위 억제효과가 나타났으며 휨모멘트에서는 4%의 보강효과가 나타났다.
(3) 케이싱 보강조건에 따라 보강효과가 각각 상이한 것으로 나타났으며 적정 케이싱 보강길이를 알아보기 위해 보강조건을 구간별로 비교한 결과 말뚝의 수평지지특성 모두 κ=0.4∼κ=1.2구간이 가장 큰 차이를 나타내어 κ=1.2조건이 가장 효율적인 보강조건으로 판단된다. κ=2.0에서 All Casing구간이 가장 작은 차이를 나타내어 All Casing조건의 경우 수평지지특성에서 가장 큰 안정성을 가지지만 가장 비효율적인 보강조건으로 판단된다.
본 연구는 단일 모래지반에서의 케이싱 보강 길이비에 따른 비선형해석을 수행한 것으로 다층지반과 말뚝의 단면변화에 대한 사항은 고려하지 않은 한계가 있다. 말뚝의 강성은 직경에 관련되어 있으며 인접지반의 특성에 의해 말뚝의 수평거동이 달라지기 때문에 다양한 지반조건 및 단면변화를 대상으로 한 추가연구가 필요할 것으로 판단된다.