1. 서 론
2. 신뢰성 이론과 목표파괴확률
2.1 한계상태 개념 및 신뢰성 분석 종류
2.2 하중저항계수설계법(LRFD: Load and Resistance Factor Design)
2.3 확률분포와 목표파괴확률
3. 무공케이슨 방파제 원호활동 신뢰성분석
4. 신뢰성해석 방법
5. 신뢰성해석에 의한 하중저항계수 산정결과
6. 결 론
1. 서 론
토목구조물의 하중과 재료는 본질적으로 불확실성을 내포하고 있으며, 특히 자연적으로 형성된 지반과 암반을 다루는 지반공학분야에서는 재료의 불확실성이 크고 평가하기 어렵다. 따라서, 지반구조물 해석에 이용되는 허용응력설계법(allowable stress design)은 재료의 불확실성과 분산특성을 고려하기에는 한계가 있다. 이러한 점을 보완하기 위해 토목구조물의 시방 및 설계기준에서는 하중과 재료의 특성을 확률론적인 접근방법을 통한 한계상태설계법(limit state design)을 이용하는 추세이다(ECS, 1994).
사면파괴는 사면의 토체의 상하 움직임으로 인해 파괴에 도달하는 것을 의미한다. 이러한 사면구조물의 안정해석 방법으로는 활동면을 따라 파괴가 일어나려고 하는 시점의 토체의 정역학적인 평형을 고려하여 안정성을 해석하는 한계평형해석(limit equilibrium analysis)이 가장 널리 사용되고 있으며, 최근에는 계산기법의 향상으로 종전에는 쉽게 접근할 수 없었던 유한요소(FEM: Finite Element Method) 또는 유한차분(FDM: Finite Difference Method)을 이용한 사면안정 평가방법이 개발되어 사용되고 있다.
이러한 해석방법에 의하여 도출되는 안전율(FS: Factor of Safety)은 사면이 파괴에 도달하거나 과도한 변형으로 인하여 더 이상 사용이 불가능한 경우를 결정하기 위하여 사용된다. 안전율은 사면의 활동면이 가지고 있는 전단강도에 대한 한계평형상태에서의 전단응력의 비를 의미한다. 따라서 이론상으로는 안전율이 1.0보다 크면 사면은 안전한 상태로 볼 수 있지만 설계에서는 허용안전율 이상이 되어야 안전한 것으로 판단한다. 이러한 허용안전율을 사용하는 것은 지반의 강도와 사면조건을 정확하게 결정할 수 없기 때문이다.
따라서, 구조물의 안정된 성능을 사용목적에 알맞도록 설계와 시공을 하고 구조물이 사용자가 원하는 수명을 다할 때까지 유지하기 위해서는 구조물 전체의 안전과 강도 등에 영향을 미치는 요소를 면밀히 분석해야 한다. 한계상태의 의미는 구조물의 파괴상태의 개념을 구조물의 사용목적과 중요도에 따라 역학적인 파괴의 정의보다는 설계목적에 따라 설계자와 사용자가 파괴상태 또는 사용한계를 정하고 이러한 기준에 맞도록 정량적, 합리적, 경제적설계를 하기 위한 방법이다.
기존의 결정론적 사면안정 해석의 경우 불확실성을 정량적으로 고려하지 않고 주관적 판단에 의한 보수적인 강도정수 및 설계기법을 통하여 고려하나 이러한 보수적인 설계가 파괴에 대한 안전을 보장하지는 않는다는 사실은 경험적으로 잘 알려져 있다(El-Ramly, 2002). 사면의 확률론적 해석에 관한 연구는 1970년대 이후 많은 연구자들에 의해 수행되었지만(Griffiths and Fenton, 2004; Mostyn and Li, 1993; Vanmarcke, 1977; Christian, 1997; Li and Lmub, 1987) 현장기술자들의 확률이론에 대한 이해 부족과 적용에 대한 자료부족 등으로 인하여 실제로 널리 적용되지는 못하고 있는 실정이다. Hassan and Wolff(1999)는 기존의 결정론적 사면안정해석 프로그램을 이용하여 확률론적 임계파괴면을 구하는 방법을 제시하였으며, Griffiths and Fenton(2004)은 탄소성 유한요소법을 사용한 확률론적 사면안정해석을 수행하였다. Low(2003)는 스프레드시트 프로그램을 이용하여 Hasofer-Lind의 신뢰성지수에 바탕을 둔 확률론적 사면안정 해석기법을 개발하여 연약지반의 사면안정해석에 적용하였다.
국내에서는 Kim and Lee(2002)이 기존의 결정론적 사면안정 해석기법에 공학적인 확률해석 기법을 결합시키는 방안을 제시하였으며, Jang et al.(2002)은 암반사면의 절토시 지반의 불확실성이 암사면의 파괴확률에 미치는 영향을 알아보기 위하여 신뢰성해석을 수행하였다.
Bae and Park(2002)과 Park et al.(2005)은 암반사면의 파괴확률산정에 관한 연구를 수행하였다. Kim and Cho(2006)은 확률론적 사면안정 해석기법을 개발하기 위하여 절편법의 일종인 Spencer의 방법을 바탕으로 한 결정론적 해석방법을 지반정수의 불확실성과 공간적 변동성을 고려할 수 있도록 확장하는 연구를 수행하였다. Cho and Park(2008)은 지반물성의 공간적 변동성을 고려한 확률론적 해석을 수행할 수 있는 절차를 제시하였다.
본 연구에서는 16개의 실제 무공케이슨 방파제의 설계자료를 수집하여, 원호활동파괴에 대한 신뢰성 분석을 수행하였다. 사면의 활동과 저항을 계산하기 위해서는 절편법의 일종인 Bishop 간편법(Bishop, 1955)을 이용 하였고, 지반 정수의 공간적인 변동성은 과거의 문헌 연구 자료와 일본에서 해양항만구조물 설계에 반영된 값을 참고하여 결정하였다.
2. 실험 재료 및 방법
2.1 한계상태 개념 및 신뢰성 분석 종류
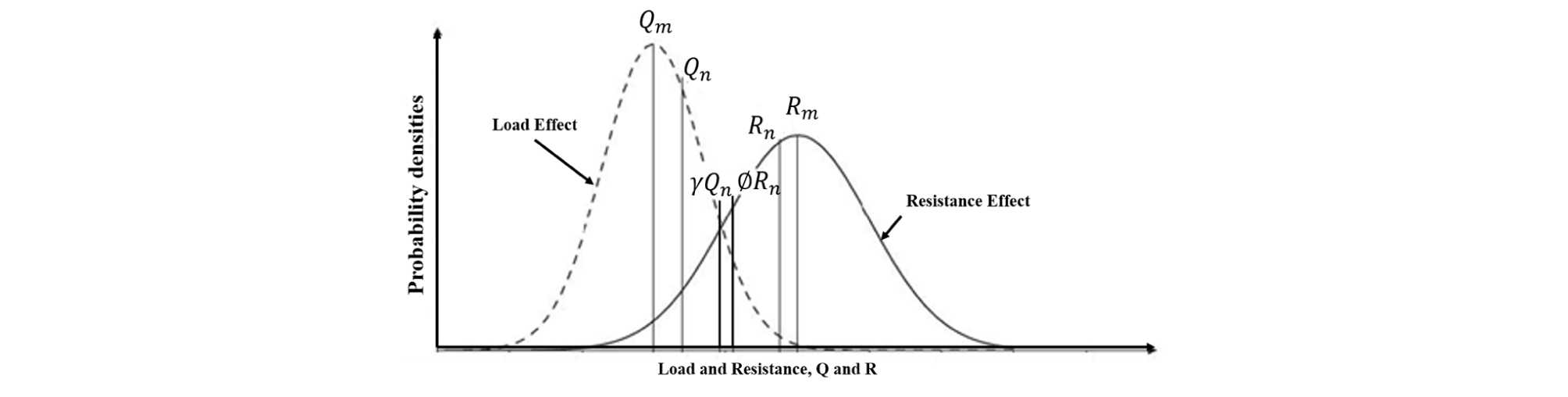
한계상태함수(limit state function)는 구조물 기초의 안전측과 파괴측에 대한 경계상태를 나타내는 한계상태를 규정하는 함수로 파괴모드에 대한 안전여유를 나타내는 성능함수(performance function)라고도 한다. 하중과 저항을 Fig. 1(a)와 같이 확률밀도함수로 나타내면, 한계상태는 식 (1)과 같이 하중과 저항의 크기가 같아지는, 즉 구조물 기초의 성능이 상실되는 상태가 된다. 또한 하중이 저항과 같거나 큰 파괴확률영역은 확률밀도함수가 겹치는 부분의 면적으로 식 (2)와 같은 파괴확률로 표현할 수 있다.
| $$g=R-Q$$ | (1) |
| $$P_f=P(R-Q\leq0)=P(g\leq0)$$ | (2) |
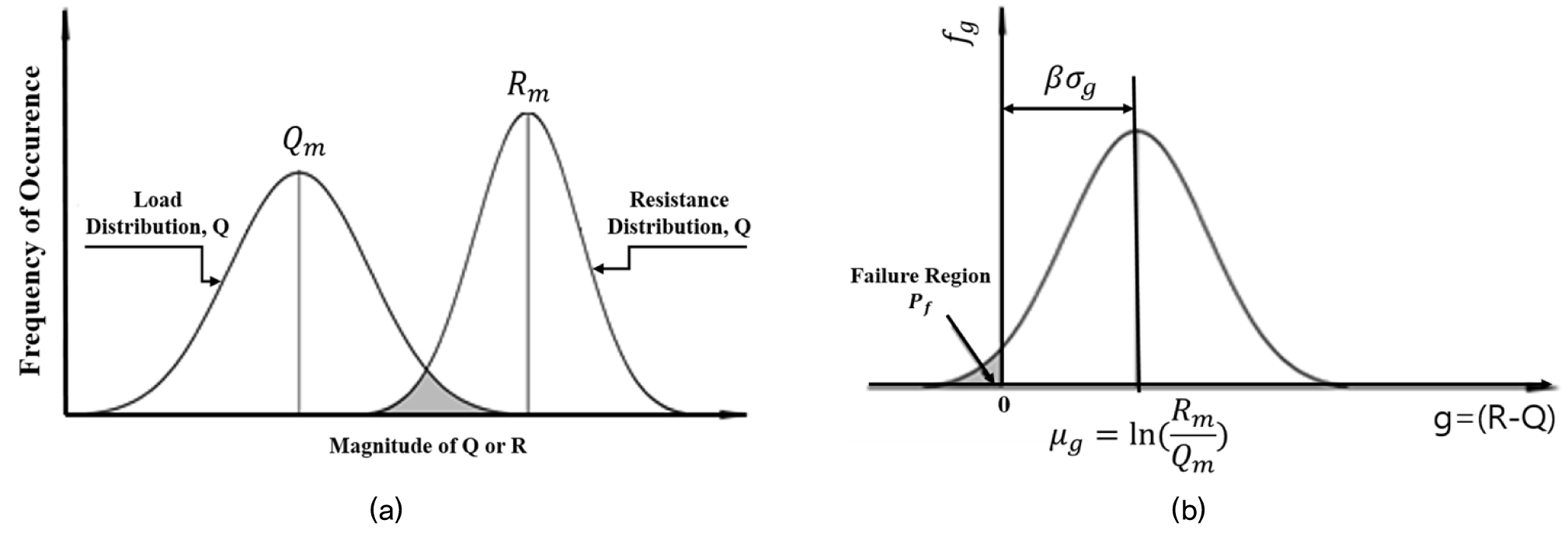
Fig. 1.
Probability of failure in reliability-based design: (a) Frequency distributions for random values of load and resistance and (b) Probability of failure (Allen et al., 2005)
신뢰도지수(β)는 한계상태함수가 g=R-Q≤0이 되는 확률로 정의되므로 확률적인 안정성을 나타내는 대표적인 척도로 사용되고 있다. 신뢰도지수는 Fig. 1(b)에서와 같이 한계상태함수의 평균(µg)이 한계상태(g=0)로부터 한계상태함수의 표준편차(σg)의 몇 배만큼의 거리를 갖고 있는가를 나타내는 지수이며, 신뢰도지수가 크다는 것은 한계상태함수의 평균값에서 한계상태까지의 거리가 멀다는 것을 의미하며, 거리가 멀수록 Fig. 2(b)에서 음영의 면적이 작아지므로 파괴확률(Pf)은 작아지는 것을 의미한다. 따라서 신뢰도지수는 한계상태 함수의 평균(µg)과 원점사이의 거리를 표준편차(σg)로 나눈 값으로 식 (3)과 같이 표현할 수 있다.
| $$\beta=\frac{\mu_g}{\sigma_g}=\frac{\mu_R-\mu_Q}{\sqrt{\sigma_R^2+\sigma_Q^2}}$$ | (3) |
Table 1은 신뢰성분석 및 해석 방법에 따른 분류(Levels Ⅰ∼Ⅲ) 예시를 정리하였다. Level Ⅲ은 신뢰함수에 확률적 개념을 그대로 적용하여 구조물의 안정성에 영향을 주는 여러 확률변수들의 상호작용을 고려하여 직접 구조물의 파괴확률을 산정하는 방법이다. 신뢰함수의 결합분포함수를 알 수 있을 때 직접 적분하여 파괴확률을 계산하는 방법과 Monte Carlo Simulation이 Level Ⅲ에 속한다. 한편 Level Ⅱ는 확률변수들이 정규분포 등과 같이 취급하기 쉬운 임의의 확률분포함수를 따른다고 가정하여, 저항함수와 하중함수의 통계적 특성, 즉, 각 확률변수의 평균 및 표준편차를 이용하여 신뢰도지수를 계산하고 이를 파괴확률로 환산시키는 해석방법이다. 마지막으로 Level Ⅰ의 해석방법은 가장 하위 단계의 신뢰성 해석방법으로 근본적으로는 Level Ⅲ나 Level Ⅱ와는 구분된다. 엄밀하게 정의하면 Level Ⅰ은 신뢰성 해석법이 라기 보다는 신뢰성 설계법이다. 즉, 임의의 파괴모드에 대하여 한계상태(극한한계/사용한계/피로한계)를 초과하는 파괴확률이 허용치 이하가 되도록 미리 결정된 각 확률변수의 부분안전계수(partial safety factor or partial coefficient)를 이용하여 설계변수를 결정하는 방법이다.
Table 1. Classification static reliability analysis method
2.2 하중저항계수설계법(LRFD: Load and Resistance Factor Design)
기존의 구조물 설계법은 시방서를 기준으로 하는 결정론적 접근법인 허용응력설계법을 사용하였다. 허용응력설계법 개념은 저항의 불확실성을 안전율의 개념을 도입하여 안정성을 경험적으로 확보하였으며, 식 (4)와 같이 구조물의 극한지지력이나 극한저항력(Rn)을 안전율(FS)로 나눈 값, 즉 허용저항력이 구조물에 작용하는 모든 하중조합(ΣQi)보다 큰 경우에 안정성이 확보된다는 것이다. 안전율은 일반적으로 오랜 기간 동안 경험적으로 축적된 자료를 바탕으로 일정 기간마다 새로운 재료, 시공방법, 경제성 등을 고려하여 구조물 기초 설계기준을 제정하는 기관과 엔지니어의 판단으로 결정된다. 이러한 안전율에 대해 유럽(ECS, 1994)을 비롯하여 캐나다 등은 외부하중과 구조물의 저항강도에 대한 설계방법을 분리하여 설계하는 부분안전계수 설계법 또는 하중계수 설계법을 연구하고 사용하여 왔다.
| $$\sum Q_i\;\leq R_{allowable}=\frac{R_n}{FS}$$ | (4) |
상부구조물 설계의 근간이 되는 구조공학분야에서는 결정론적 허용응력설계법 보다는 재료의 소성거동을 고려하여 다양한 설계변수에 대한 오차를 설계에 합리적으로 고려하기 위한 한계상태설계법의 중요성이 인정되면서 설계기준에 반영되었으며, 최근에는 상하부 구조물의 일관된 설계를 위하여 하부구조물인 지반구조물에도 그 적용성을 검토하고 있다.
미국의 고속도로협회(AASHTO, 2018)에는 기존 구조물 기초에 대한 안전율의 분포를 고려하여 허용응력설계법의 안전율을 하중저항계수설계법에 적용하는 방법이 수록되어 있다. 허용응력설계법의 안전율을 이용한 저항계수 보정방법은 기술자들이 간단하게 접근할 수 있기 때문에 쉽게 사용할 수 있으며, 기존의 안전성을 그대로 확보하면서 하중저항계수설계법(LRFD)의 저항계수를 결정하는 방법이다. 그러나 저항의 불확실성을 정량적으로 반영할 수 없으므로 저항의 통계적 특성자료를 수집하기 어려운 구조물 기초에 적용되거나 하중저항계수설계법의 도입기에 주로 이용되었다. 사하중과 활하중으로 구성된 하중저항계수의 기본 설계조건식은 식 (5)와 같으며, 허용응력설계법의 안전율은 식 (6)과 같이 나타낼 수 있다.
| $$\Phi R_n\geq\gamma_{QL}Q_L+\gamma_{QD}Q_D$$ | (5) |
| $$\frac{R_n}{FS}\geq Q_D+D_L$$ | (6) |
여기서, FS는 안전율, Φ는 저항계수, Rn는 공칭저항, QD, QL는 사하중, 활하중, γQD, γQL는 사하중, 활하중에 대한 하중계수이다.
확률이론을 바탕으로하는 하중저항계수설계법은 하중과 저항의 불확실성을 설계에 반영하고, 상부 구조물과 구조물 기초의 신뢰도 수준에 따라 저항계수를 보정하기 위하여 개발되었다. 기존의 허용응력설계법에서 경험적으로 적용되던 안전율을 이용한 저항계수 보정방법과는 달리 신뢰성이론을 적용할 경우에는 설계 시 저항값을 예측하는 이론식에 내재된 보수성과 저항의 불확실성을 저항편향계수의 개념을 도입하여 정량적으로 고려할 수 있으며, 구조물 기초의 형식 및 제반 여건 하에서 가장 적합한 이론식을 규명할 수 있는 장점이 있다. 그러나 실측자료의 수집, 데이터베이스의 구축, 통계학적 분석 및 신뢰성이론의 적용에 익숙하지 않은 기술자들은 근본적인 내용에 접근하기 어려운 단점이 있다. 신뢰성이론을 이용한 저항계수 보정방법에서는 구조물 기초의 구조적 안전여유를 신뢰성해석 등에 의한 기초의 신뢰도 수준 범위와 상부 구조물의 신뢰도 수준을 고려하여 목표신뢰도지수(βT)로 적용하므로 전체구조 시스템에 일관된 안전여유를 부여할 수 있다. 본 연구에서는 목표신뢰도지수에 대한 하중 및 저항 계수를 제시하고 있지는 않지만, 하중 및 저항 계수를 산정하기 위한 필수 조건인 정밀 신뢰성분석을 통하여 16개의 실제 무공케이슨 방파제 원화활동 설계사례에 대하여 신뢰도지수 및 파괴확률을 평가하였다.
2.3 확률분포와 목표파괴확률
하중저항계수설계법에서 하중(Q)과 저항(R)은 통계학적으로 독립이며, Fig. 2와 같이 평균(µQ, µR)과 표준편차(σQ, σR)를 갖는 정규분포 또는 로그정규분포 확률밀도함수(fQ, fR)로 간주한다. 하중과 저항의 불확실성은 평균값을 중심으로 얼마나 가깝게 혹은 넓게 분포하는가에 대한 분산의 척도를 파악할 필요가 있으며, 식 (7)과 식 (8)과 같이 산포도의 척도나 변동성의 무차원적 척도를 나타내는데 편리하게 이용되고 있는 변동계수(coefficient of variation, COV)로 표현할 수 있다.
| $$COV_Q=\frac{\sigma_Q}{\mu_Q}$$ | (7) |
| $$COV_R=\frac{\sigma_R}{\mu_R}$$ | (8) |
신뢰성이론에서 하중과 저항은 대표값을 중심으로 이산성을 나타내는 확률변수로 간주하며, 신뢰성이론을 이용한 하중저항계수설계법에서는 하중과 저항의 확률밀도분포를 로그정규분포로 가정하고 있다. 로그 정규분포는 확률변수(x)의 값이 항상 양에 대하여 정의되므로, 음의 값이 될 수 없는 하중 및 저항의 물리량을 나타내는데 유용하게 적용될 수 있다. 로그정규분포는 확률통계학에서 가장 많이 사용되고 있는 정규분포와 대수의 관계를 가지고 있으므로 표준 정규확률분포로부터 편리하게 이용할 수 있다(Kim, 2014).
무공케이슨 방파제 제체의 원호활동에 대한 하중 및 저항계수를 산정하기 위해서 대표적인 사면안정 해석법인 비숍 간편법을 사용하였다. 이전에 방파제 구조물에 대한 목표신뢰도지수 또는 목표파괴확률을 제시하는 선행연구가 없어, 본 연구에서는 사면의 허용파괴확률을 무공케이슨 방파제 제체 원호활동의 목표신뢰성 지수를 결정하는데 참고하였다. Table 2는 Santamarina et al.(1992)가 제시한 사면의 적정 허용파괴확률이다.
Table 2. Acceptable probability of failure for slopes (Santamarina et al., 1992)
무공케이슨 방파제의 목표신뢰도지수의 경우, 사고나 손상에 관하여 통계자료를 근간으로 하여 사고 손상이 1년간에 발생하는 확률을 계산하여 이것을 참고로 하여 결정하는 방법, 기존구조물의 신뢰도수준 평가에 의한 방법, 구조물의 파괴와 함께 예측되는 사망위험성을 피해 위험도와 비교에 의한 방법, 인적 손실에 대한 위험도 저감에 필요한 투자 효과에 의한 방법, 생애주기비용(LCC: Life Cycle Cost) 최소화기법에 의한 방법 등에 의하여 결정되어야 한다(Ministry of Oceans and Fisheries, 2005). 방파제 구조물의 파괴가 발생할 경우, 직접적인 인명 피해가 발생할 가능성은 적다. 하지만 파도의 영향으로 근접 지역에 피해를 줄 수 있기 때문에 인구 밀집도 또는 시설의 밀도 등과 같은 지역 특성에 따라 합리적인 목표파괴확률 또는 목표신뢰도지수를 결정하는 것이 중요하다(Foye, 2004; Ellingwood et al., 1980; and NCHRP 2004). 따라서, 본 연구에서는 목표신뢰도지수를 넓은 범위로 설정하고자 하며, 목표신뢰도지수 2.0(Pf=0.023), 2.5(Pf=0.006), 3.0(Pf=0.001)에 대한 하중 및 저항계수를 제시하였다.
3. 무공케이슨 방파제 원호활동 신뢰성분석
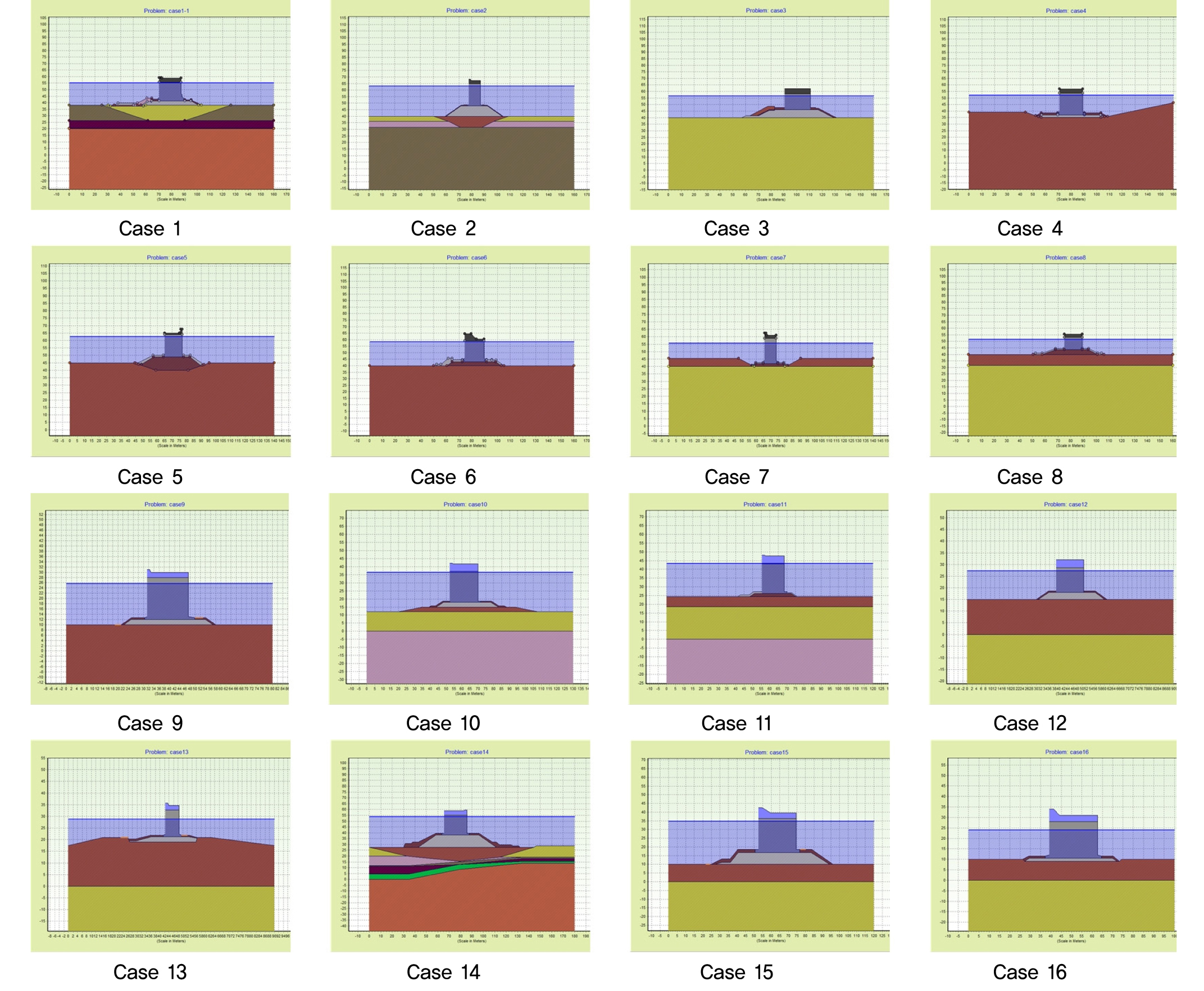
본 연구에서는 16개의 무공케이슨 방파제를 대상으로 설계자료에 대한 상시와 지진시 조건에서의 신뢰성해석을 수행하였다. 연구대상 16개 지역의 방파제의 상부구조물 및 하부지반조건이 반영된 설계자료를 바탕으로 신뢰성 해석을 수행하였고, 현행 설계법으로 시공된 무공케이슨 방파제 제체의 원호활동에 대한 신뢰성 지수를 산정하였다. Fig. 3은 연구대상 16개 지역의 방파제를 모델링한 것이다.
무공케이슨 방파제 모델링은 하부지층과 상부구조물로 나뉘며 각 지층의 점착력, 내부마찰각, 단위중량은 불확실성을 고려한 확률변수로 분석을 수행하였다. 설계변수 변동성은 지역 및 지층조건에 따라 달라지기 때문에 이를 객관적으로 정량화하기 어렵고, 상치 콘크리트 상부에 작용하는 재하량과 지진 해석시 적용하는 지진계수에 대해서도 불확실성을 가지는 변수이기 때문에 이에 대한 편향계수와 변동계수도 결정해야 한다. 일본 해양항만구조물 설계에서는 무공케이슨 방파제 설계변수에 대하여 Table 3과 같이 가정하고 있으며, 본 연구에서는 설계변수의 변동계수로 적용하였다.
Table 3. Uncertainties of soil parameters, traffic load, and horizontal seismic coefficient of pseudostatic approach for open cell caisson breakwater reliability analysis (Overseas coastal area development institute of Japan, 2018)
4. 신뢰성해석 방법
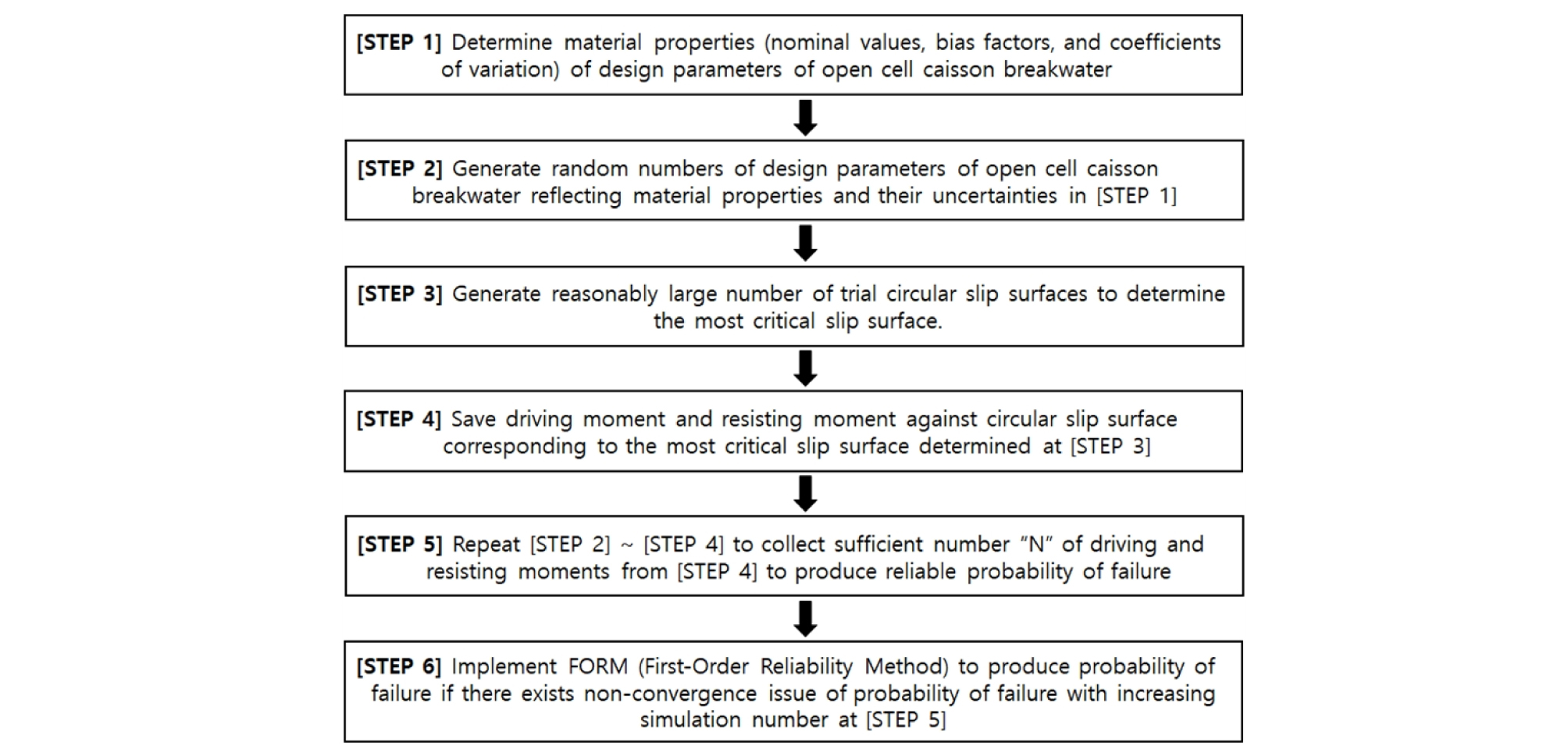
원호활동에 대한 신뢰성해석은 Level III 방법인 Monte Carlo Simulation을 통하여 신뢰도지수를 계산하거나 Monte Carlo Simulation과 FORM을 조합하여 계산하였다. 지층의 지반정수, 단위중량 등의 각 불확실성을 고려한 사면에 대하여 가장 취약한 가상파괴면을 찾아야하기 때문에 복잡한 과정을 필요로 한다. 자세한 파괴확률 산정은 다음과 같은 절차(Fig. 4)에 따라 결정된다. [1단계] 각 무공케이슨 방파제의 설계변수 값과 불확실성(편향계수와 변동계수)을 결정한다. [2단계] 1단계의 설계변수 값과 변동계수를 반영하고 난수를 발생시긴 설계변수 값을 사면해석프로그램에 입력한다. [3단계] 하부 제체부에 충분히 많은 원호 가상파괴면을 발생시켜, 최소안전율을 갖는 원호 가상 파괴면을 찾는다. [4단계] 3단계에서 결정된 원호 가상 파괴면에 대한 저항모멘트와 하중모멘트를 별도로 계산한다. [5단계] 안정된 파괴확률을 산정하기 위해 2단계~ 4단계를 반복 수행한다. 반복수행 된 저항모멘트/하중모멘트 비, 하중모멘트와 저항모멘트를 오름차순으로 정리하여 전체회수(N) 대비 파괴 회수(n; 저항모멘트/하중모멘트 비가 1보다 작은 회수)으로 파괴확률을 계산하고, 도출된 결과를 활용하여 신뢰성지수를 계산한다. 하지만 파괴확률이 아주 낮을 경우 Monte Carlo Simulation을 통해 수렴하는 파괴확률을 확인하기 어려울 수 있다. 이러한 경우에는 [6단계]와 같이 FORM을 이용하여 하중모멘트와 저항모멘트의 분포 및 하중모멘트와 저항모멘트의 상관계수를 반영하여 신뢰도지수 또는 파괴확률을 평가한다.
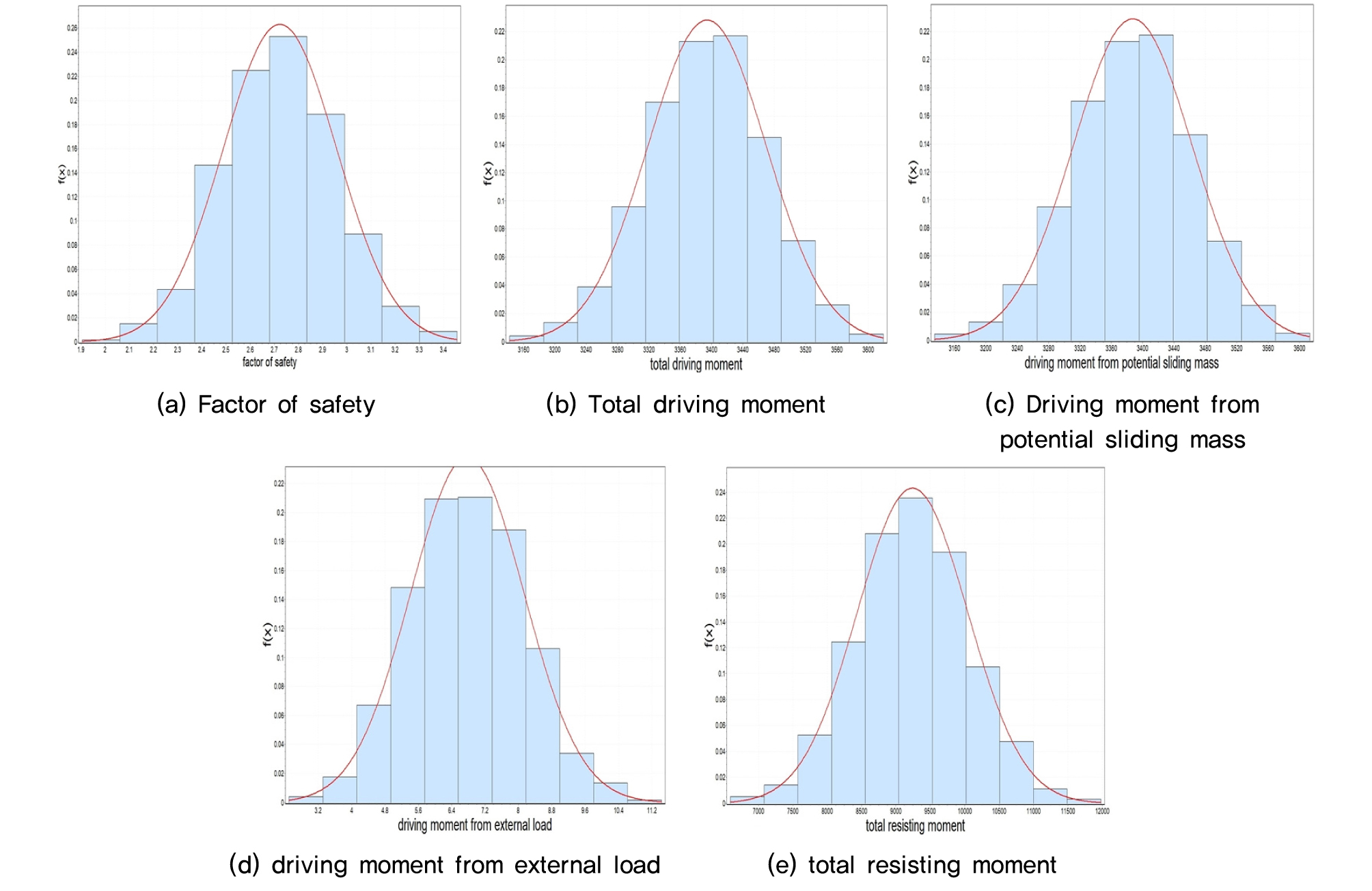
시뮬레이션을 통한 파괴확률 산정절차에 따라 결정론적인 해석과 동일한 조건으로 기존 설계된 16개의 무공케이슨 방파제의 원호활동에 대한 신뢰성 분석을 해 본 결과, 계산된 신뢰성지수는 4이상으로 파괴확률이 아주 낮은 것으로 나타났다. 신뢰성 분석 결과로부터 도출된 안전율 분포, 전체 활동모멘트 분포, 토체에 의한 활동모멘트의 분포를 나타내었다(Fig. 5).
5. 결 론
무공케이슨 방파제 설계자료에 기초하여 상시와 지진시 조건에서의 신뢰성해석을 수행하였다. 지반정수, 단위중량, 외력의 불확실성은 Table 3의 값으로 가정하였다. 4절에 소개된 절차를 따라 해석을 한 결과, Table 4와 Table 5와 같이 산정되었다. Table 4는 상시 해석결과로 결정론적 해석법으로 산정한 하중 저항모멘트와 Monte Carlo Simulation을 통하여 산정된 하중 저항의 확률변수와 상관성을 나타낸 것이다. Table 5는 지진시 결과를 나타낸 것이다.
Table 4. Results of limit equilibrium analysis and reliability analysis of open cell caisson breakwater against circular failure for sixteen design cases under ordinary condition (here, MQ and MR are driving and resisting moments, respectively)
Table 5. Results of limit equilibrium analysis and reliability analysis of open cell caisson breakwater against circular failure for sixteen design cases under seismic condition (here, MQ and MR are driving and resisting moments, respectively)
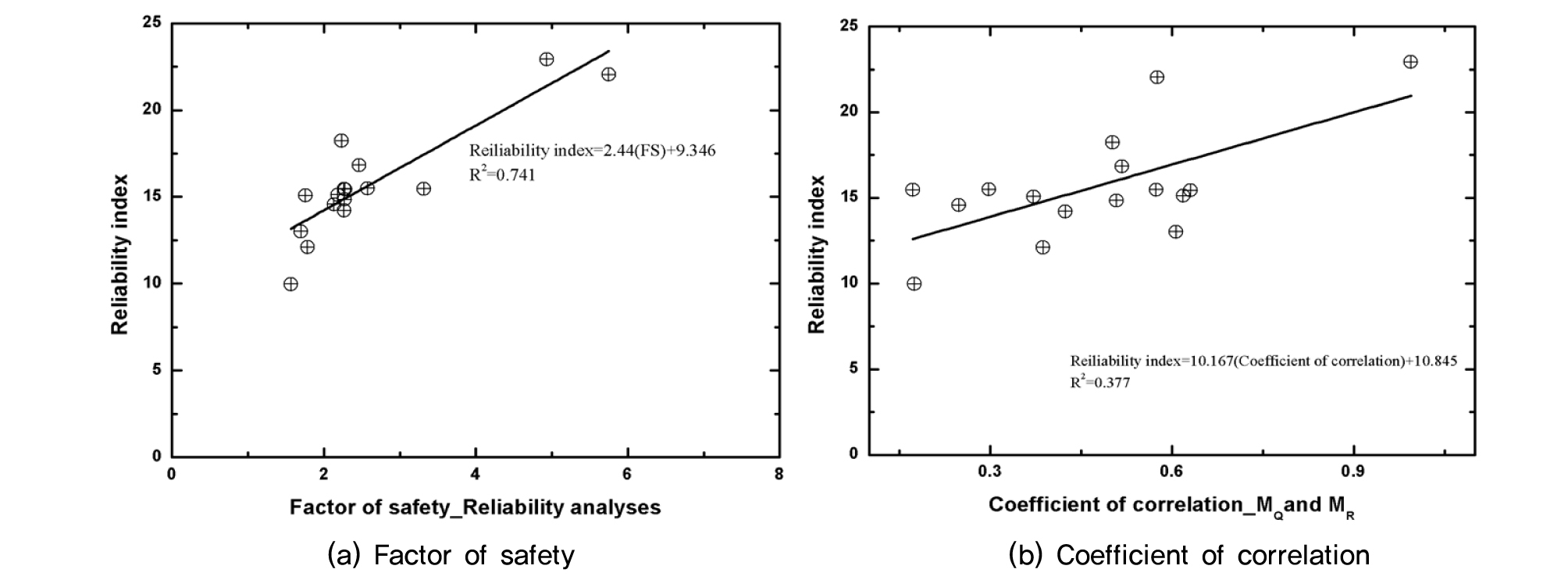
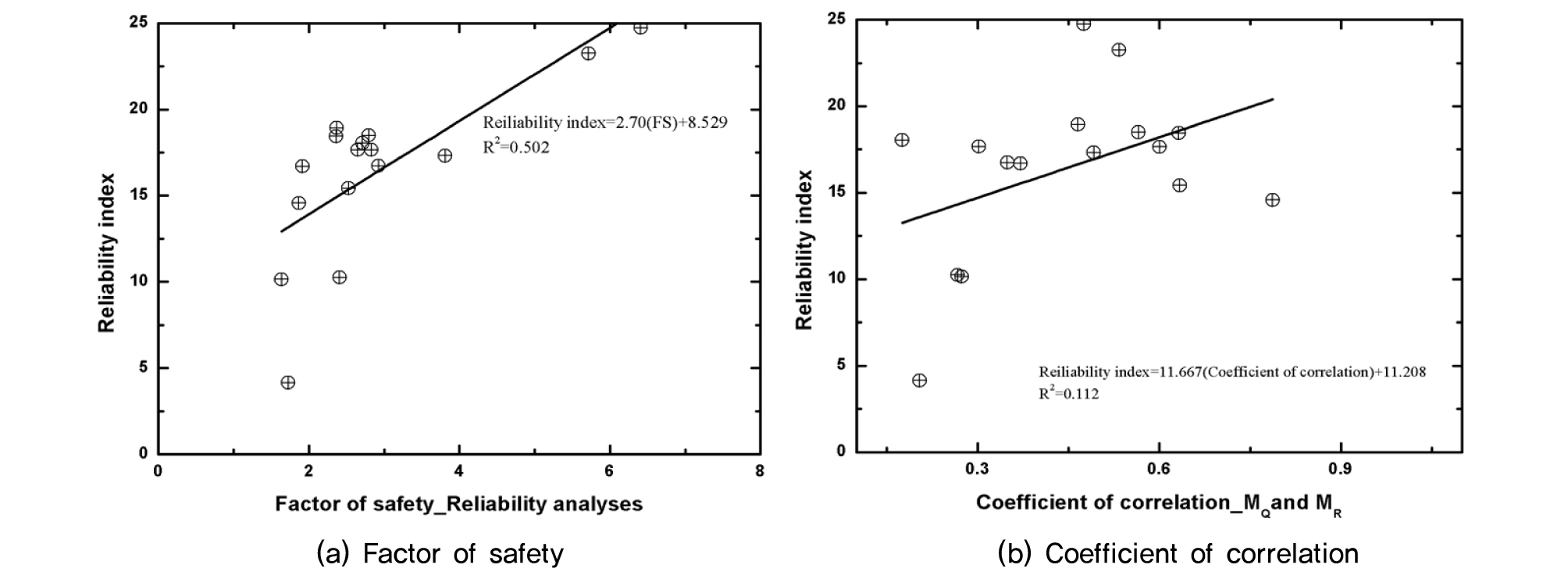
Fig. 6과 Fig. 7은 각각 상시와 지진시 경우에서 (a) 안전율 변화에 따른 신뢰성지수의 변화의 관계와 (b) 하중모멘트와 저항모멘트 사이의 상관계수에 따른 신뢰성 지수를 도식화한 것이다. 상시 조건에서는 안전율과 하중모멘트와 저항모멘트 사이의 상관계수는 신뢰성지수와 양의 상관관계가 도출되는 것을 확인할 수 있다(Fig. 6(a)과 6(b)). 표면상으로는 지진시의 “안전율과 신뢰성지수”, “하중모멘트와 저항모멘트 사이의 상관계수와 신뢰성지수”의 각각의 상관관계가 상시의 양의 관계보다 높은 것(기울기의 크기)으로 보이지만, R2 값은 상시의 경우가 지진시의 경우보다 더 크다(Fig. 7(a)과 8(b)). 이는 토체 전체를 수평으로 흔드는 힘인 지지력이 불확실성도 크고 힘의 크기도 크기 때문에 무공케이슨의 안정성에 미치는 영향이 크기 때문이다.
산정된 결과를 바탕으로 결정론적 해석에 의한 결과와 신뢰성 해석에 의한 결과에 따른 안전율과 신뢰도지수를 상시와 지진시의 경우에 대하여 Table 6과 같이 산정하였다. 설계자료에 의한 신뢰성 해석결과 계산된 신뢰성 지수가 높은 것은 구조물의 파괴확률이 매우 낮음을 의미한다. 또한, 제체의 원호활동의 허용최소안전율이 1.3인 것에 비하여 안전율이 모두 높게 산정된 것으로 보아 매우 보수적으로 설계된 것으로 판단되었다.
Table 6. Factors of safety and reliability indices of open cell caisson breakwater against circular failure for sixteen design cases under ordinary and seismic conditions
6. 결 론
본 연구는 허용응력설계방법과 확률개념을 적용하여 무공케이슨 방파제에 대한 하중저항 설계의 신뢰성을 분석하여 무공케이슨 방파제 구조물의 신뢰성 지수를 산정하고, 원호활동의 신뢰성 분석방법을 제시할 목적으로 수행하였다. 원호활동의 신뢰성 분석을 위해 Monte Carlo Simulation을 적용하였고, 적용된 지반강도정수의 불확실성을 고려한 검토를 수행하였다. Monte Carlo Simulation으로 안정된 파괴확률을 도출하기 어려운 경우에는 Monte Carlo Simulation 결과를 바탕으로 FORM을 수행하여 신뢰도지수 및 파괴확률을 평가하였다. 시뮬레이션을 통한 파괴확률 산정절차에 따라 결정론적인 해석과 동일한 조건으로 신뢰성 분석을 해 본 결과, 계산된 신뢰성지수는 일반적으로 지반구조물에서 적용하는 목표신뢰성지수(2∼3)에 비하여 매우 높게 산정되어 파괴확률이 아주 낮은 것으로 나타났다. 또한, 안전율 분포, 전체 활동모멘트 분포, 토체에 의한 활동모멘트의 분포는 모두 정규확률분포를 나타내는 것으로 확인하였다. 무공케이슨 방파제의 원호활동에 대한 신뢰성지수는 강도정수의 변동성 및 하중과 저항의 상관성에 가장 큰 영향을 미치는데 이에 대한 합리적인 가정이 필요할 것으로 사료된다. 본 연구에서는 일본 항만기준에서 제시하는 설계변수의 변동성을 적용하였으며, 실제 설계에서도 유사한 설계변수 변동성을 가지도로고 품질관리 및 지반층 분할 등이 필요하다.