1. 서 론
2. 수치해석 개요
2.1 수치해석 방법
2.2 수치해석 검증
2.3 포장층 두께와 교통하중 크기를 고려한 수치해석
3. 포장층 두께와 교통하중 크기를 고려한 수치해석 결과
4. 포장층 두께와 교통하중의 크기를 고려한 지반 안전율 분석
4.1 응력비 분포와 지반 안전율 상관관계 분석
4.2 지표침하량과 공동직경의 상관관계 분석
4.3 지표침하량과 비파괴심도의 상관관계 분석
4.4 비파괴심도와 공동직경의 상관관계 분석
5. 결 론
1. 서 론
최근 도심지에서 자주 발생하고 있는 지반함몰은 지중에서 발생된 공동이 주요 원인인 것으로 많은 연구를 통해 확인된 바 있다. 이러한 공동은 지반굴착, 지중매설관, 주변 지반의 다짐불량, 관거 파손 및 급격한 지하수 유동과 같은 지반의 안정성을 저해하는 원인자에 기인한다(You et al., 2019).
You et al.(2018)는 유한요소해석을 통해 하수관거 파손에 따른 토사유실로 인해 발생되는 지중 공동이 지표침하에 미치는 영향에 대해 파손 폭과 토피고를 고려하여 정량적으로 분석한 바 있으며, Oh et al.(2015)는 유한요소해석 방법을 기반으로 파손된 하수관의 누수로 인해 발생되는 지하 공동의 진행에 따른 지표침하량, 지표면의 영향범위 등과 같은 지반거동을 분석하였다. Lee et al.(2018)는 유한요소해석을 통해 서울시에서 제시한 공동관리 등급제의 기준 요소인 아스팔트 포장층의 두께, 토피고, 공동 폭 및 공동 높이를 영향인자로 하여 하중조건에 따른 상관관계를 분석하였다. 또한 Yoon et al.(2016)은 유한차분해석을 통해 도시철도 인접지반에서 공동이 발생한 경우 지하수위에 유무에 따른 노반침하량 분석을 통해 노반 안정성 평가를 수행한 바 있으며, Kim et al.(2018)은 개별요소법을 통해 지반함몰의 유형을 포화상태에 따라 분류하고 각 유형에 대해 상대밀도에 따른 해석을 수행하여 지하수위 및 표면 침하에 따른 지반함몰 발생 거동을 분석한 바 있다.
한편, Kim and Heo(2016)은 축소모형실험을 통해 석회암 공동 상부에 존재하는 구조물 기초의 안정성을 공동의 분포상태와 지반침하 관계로 검토한 바 있으며, Jee and Kim(2000)는 모형실험을 통해 심도별 지하공동의 점진적인 붕락이 지표침하에 미치는 영향을 분석하여 침하예측방법을 제안한 바 있다. 또한 Park and Choi(2019)는 공동구간의 FWD(Falling Weight Deflectometer) 처짐값에 역산기법을 적용하여 아스팔트 포장체의 물성을 파악하고, 공동구간 도로포장체의 지지력 저하 정도를 평가하였다.
국외의 경우, Kuwano et al.(2010) 실내모형실험을 통해 지하수위가 하수관거 파손으로 인해 발생된 공동에 미치는 영향을 분석하였고, Mukunoki et al.(2012)는 X-ray CT 스캐너를 사용하여 파손된 하수관으로부터 물의 유입 및 토사유출로 인한 공동 및 파괴 메커니즘에 대하여 분석하였다.
이와 같이, 기존의 연구사례를 보면 지중공동 발생 메커니즘 분석 및 공동의 규모가 지반침하에 미치는 영향 분석과 관련한 연구가 대다수이고, 다양한 공동 발생 지반조건에서의 포장층 두께 및 교통하중 크기 변화에 따른 지반의 전반적인 안정성 분석에 대한 연구는 미흡한 실정이다.
따라서, 본 연구에서는 공동 발생 지반의 안정성을 분석하기 위해 포장층 두께와 교통하중 크기의 변화를 고려한 유한요소 수치해석을 수행하였다. 수치해석 모델의 검증을 위해 선행연구(Park and Choi, 2019) 결과와 비교하였으며, 기존의 연구결과(You et al., 2019)를 활용하여 공동 발생 지반의 역학적 거동을 모사하였다. 수치해석 결과로부터 지반의 간극비, 지표침하, 전단응력의 변화를 확인함으로써 전반적인 지반의 역학 거동을 확인할 수 있었으며, 본 연구에서 산정한 응력비 및 비파괴심도와 지표침하량의 관계를 이용하여 공동 발생 지반의 안정성을 분석하였다.
2. 수치해석 개요
2.1 수치해석 방법
본 연구에서는 공동 발생 지반의 역학적 거동을 모사하고 지반의 전반적인 안전성을 분석하기 위하여 PLAXIS 2D를 이용한 유한요소 수치해석을 수행하였다. 수치해석에 적용된 물성 및 역학모델, 경계조건 등은 선행연구(You et al., 2019)를 토대로 결정하였으며, 모델지반 상부에 포장층을 추가적으로 모델링하고 교통하중을 적용함으로써 그 변화에 따른 지반의 역학 거동을 파악하고자 하였다.
전술한 지반의 역학모델은 실제 지반의 탄소성거동을 면밀히 재현할 수 있도록 비선형탄성모델을 탄소성이론으로 확장한 Hardening Soil model(Schanz et al., 1999)을 적용하였다.
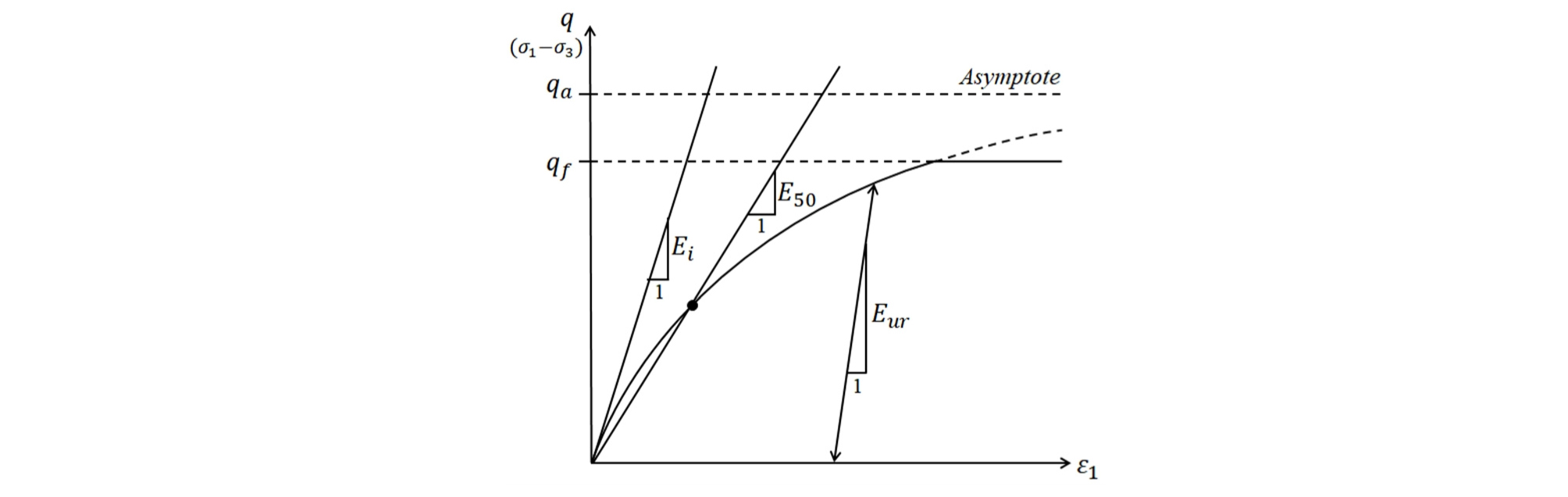
Hardening soil model에서 축변형률(ϵ1) 축차응력(q)의 관계를 나타내면 식 (1)과 같다. 여기서, qa는 수렴 축차응력, qf는 극한 축차응력을 나타낸다.
| $$\in_1=\frac{q_a}{2E_{50}}\;\frac{(\sigma_1-\sigma_3)}{q_a-(\sigma_1-\sigma_3)}\;\;\;\;\;\;\;\;\;\mathrm{for}\;\;\;\;\;\;\;q\prec q_f$$ | (1) |
상기의 식을 응력과 변형률의 관계로 나타내면 Fig. 1에 나타낸 바와 같으며, 여기서 하중 증가(loading)에 따른 E50과 제하중(unloading) 또는 재하중(reloading)에 대한 Eur은 각각 식 (2)와 식 (3)과 같이 표현된다.
| $$E_{50}=E_{50}^{ref}\;{(\frac{\sigma_3+c\cot\;\phi_p}{\sigma^{ref}+c\cot\phi_p})}^m$$ | (2) |
| $$E_{ur}=E_{ur}^{ref}\;{(\frac{\sigma_3+c\cot\;\phi_p}{\sigma^{ref}+c\cot\phi_p})}^m$$ | (3) |
여기서, 는 하중 증가 시 기준 구속압 σref에 대응하는 기준 탄성계수, m은 구속압에 대한 계수(일반적으로 0.5 적용)이다. 또한 는 재하 또는 제하 시 기준 구속압 σref에 대응하는 기준 탄성계수로서, 일반적으로 값을 적용한다.
한편, 본 모델에서는 삼축응력 상태에서 다음과 같은 두 가지 항복함수를 정의하고 있다.
| $$f_{12}=\frac{q_a}{E_{50}}\frac{(\sigma_1-\sigma_2)}{q_a-(\sigma_1-\sigma_2)}-\frac{2(\sigma_1-\sigma_2)}{E_{ur}}-\gamma^p$$ | (4) |
| $$f_{13}=\frac{q_a}{E_{50}}\frac{(\sigma_1-\sigma_3)}{q_a-(\sigma_1-\sigma_3)}-\frac{2(\sigma_1-\sigma_3)}{E_{ur}}-\gamma^p$$ | (5) |
여기서, γp는 소성전단변형률을 나타내고 있으며 다음과 같이 정의된다.
| $$\gamma^p=\varepsilon_1^p-\varepsilon_2^p-\varepsilon_3^p$$ | (6) |
또한, 소성변형률증분은 식 (7)과 (8)에 나타내는 소성포텐셜함수와 흐름법칙에 의해 결정된다.
| $$g_{12}=\frac{(\sigma_1-\sigma_2)}2-\frac{(\sigma_1+\sigma_2)}2\;\bullet\;\sin\;\Psi_m$$ | (7) |
| $$g_{13}=\frac{(\sigma_1-\sigma_3)}2-\frac{(\sigma_1+\sigma_3)}2\;\bullet\;\sin\;\Psi_m$$ | (8) |
여기서, ψm은 다일러턴시 각을 나타내고 있다.
한편, Table 1은 본 수치해석에 적용한 지반정수를 나타낸 것으로, 이는 Benz(2007)가 일반적인 사질토 재료에 대하여 제시한 값을 참고하여 결정하였다.
Table 1. Soil parameters of hardening soil model in FEA
| (kPa) | (kPa) | (kPa) | c (kPa) | ϕ΄ (°) | ψ (°) | γ (kN/m3) |
| 16,000 | 22,000 | 90,000 | 0 | 37 | 1.5 | 18.0 |
2.2 수치해석 검증
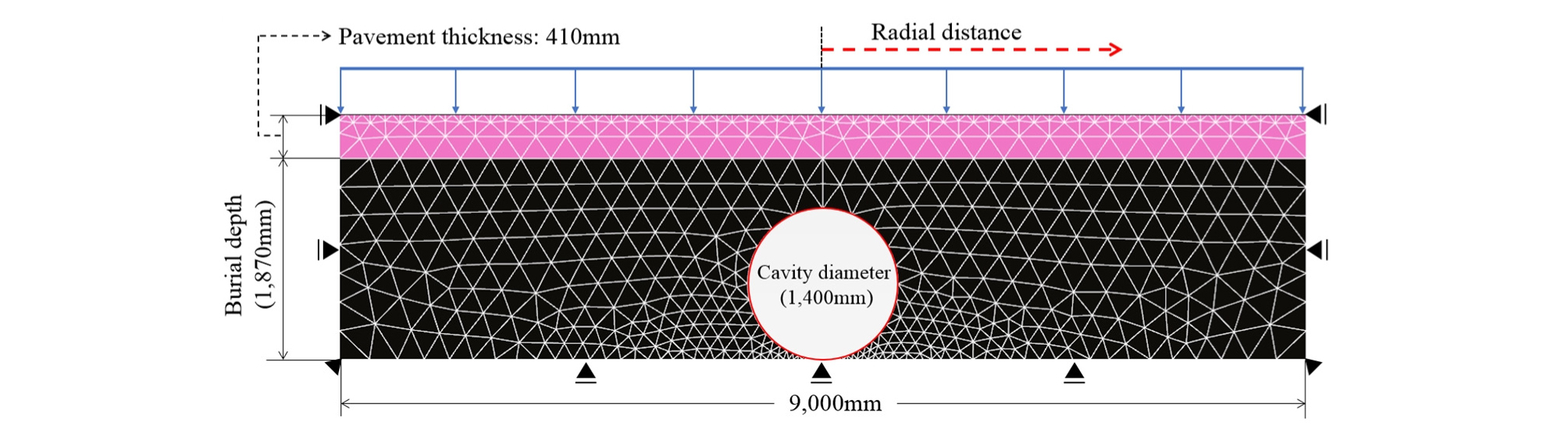
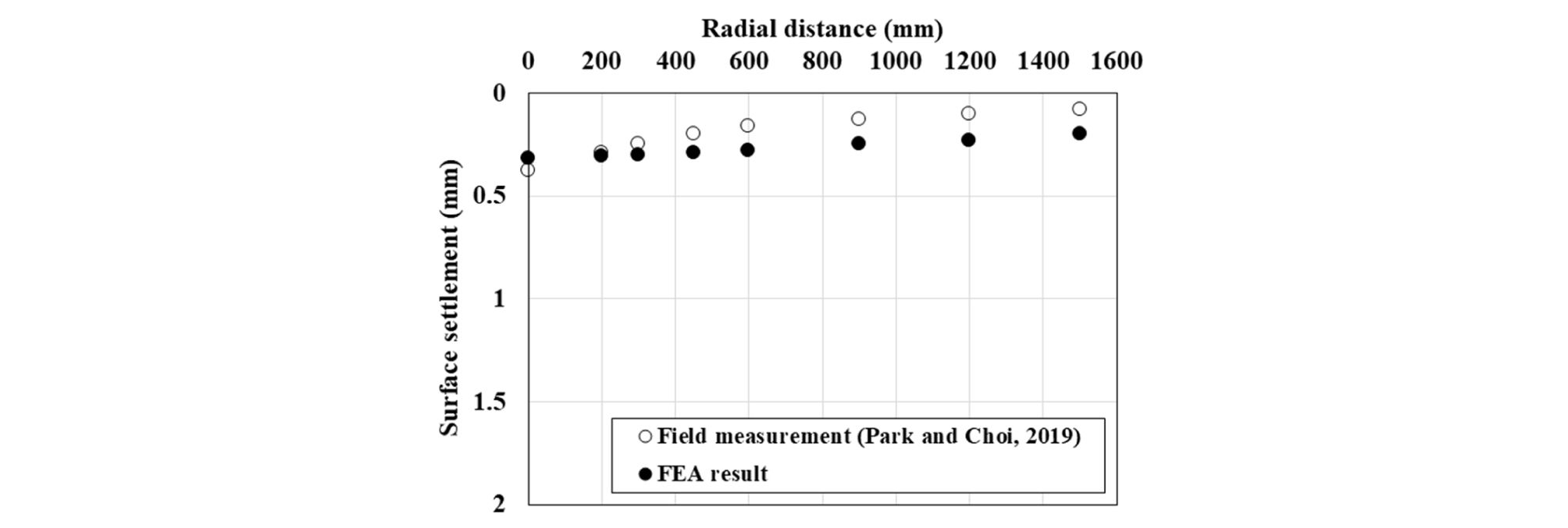
본 연구에서 수행하는 수치해석의 방법과 그 결과의 신뢰성을 검증하기 위하여 공동이 발생 된 지반의 현장계측 결과(Park et al., 2019)를 활용하여 비교·분석하였다. 계측결과로부터는 GPR 조사로 파악된 1개소의 공동 지점에 대한 도로 포장층의 처짐(지표침하) 계측 정보를 활용하였다. Fig. 2은 계측 지점의 공동 규모, 공동발생 심도, 포장층 두께를 고려한 수치해석 모델을 나타내고 있다. 수치해석 결과, 공동 중심의 지표면에서 가장 큰 침하가 발생하였으며 공동 중심에서 멀어질수록 그 발생량은 감소함을 알 수 있었다(Fig. 3). 또한, 수치해석과 계측의 결과는 상호 유사한 값을 나타내고 있음을 알 수 있으며, 이러한 결과로부터 본 연구에서 적용하는 수치해석 방법은 공동 발생 지반의 역학거동을 모사하기에 신뢰성이 확보되었다고 판단할 수 있다.
2.3 포장층 두께와 교통하중 크기를 고려한 수치해석
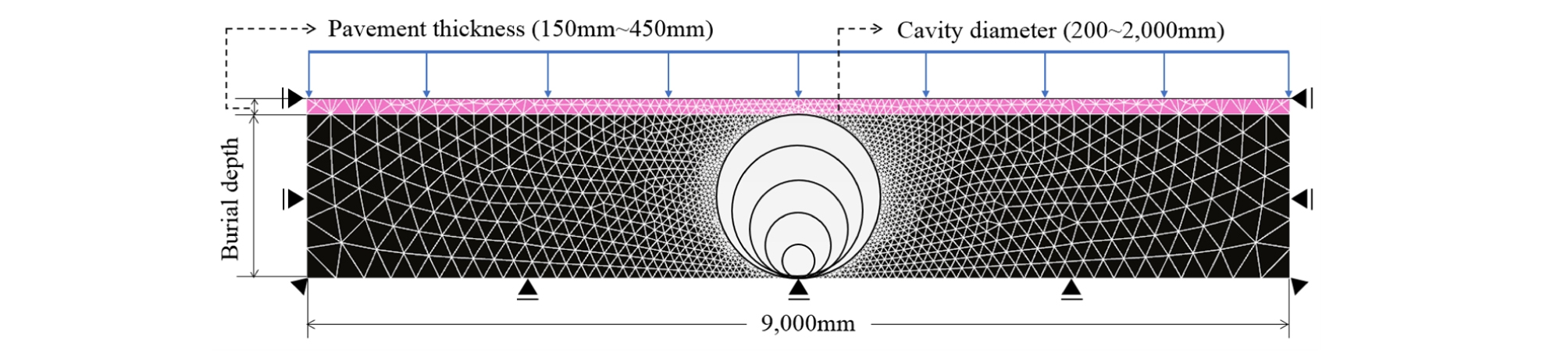
본 연구에서는 공동 발생 지반에 대하여 포장층 두께와 교통하중 크기를 고려한 지반의 안전성을 분석하기 위하여 일련의 수치해석을 수행하였다. Fig. 4은 본 수치해석의 지반 모델을 나타내고 있다. 수치해석에서는 모형지반의 측면부 구속에 대한 영향을 최소화하기 위하여 지반 폭을 9,000mm로 확대 적용하였으며, 모형지반에서 포장층 두께를 제외한 높이를 매립심도로 정의하였다. 또한, 지중에 발생되는 공동은 실제로 다양한 형상으로 발생될 수 있으나, 본 연구에서는 기하학적으로 이상적인 원형의 형태로 가정함으로써 공동 주변 지반에 발생되는 응력과 변형에 대하여 안정적인 해석이 수행될 수 있도록 모델링하였다. 본 수치해석에서의 매립심도는 1000mm∼2,000mm, 공동의 직경은 200mm∼1,000mm, 포장층 두께는 150mm∼450mm, 교통하중은 12.7kN/m2∼38.1kN/m2의 범위로 변화시키며 해석을 수행하였다(Table 2). 한편, 그 밖의 지반 모델 경계조건과 역학모델, 지반 물성치 등은 앞 절에 서술한 바와 동일한 조건으로 수행하였다.
Table 2. FEA cases
3. 포장층 두께와 교통하중 크기를 고려한 수치해석 결과
Fig. 5에서 Fig. 7은 본 수치해석 결과로부터 얻은 매립심도 1,500mm, 포장층 두께 150mm, 교통하중 12.7kN/m2이 적용된 조건에 대한 공동 직경에 따른 공동 주변 지반의 간극비, 지표면 침하량, 전단응력 분포를 나타내고 있다. 초기간극비가 0.7인 본 해석에서 지반의 간극비는 공동 주변을 중심으로 변화가 발생하고 있으며, 공동 크기와 관계없이 모든 경우에서 공동 상단부에 간극비의 감소, 하단부에 증가 현상이 나타나고 있음을 알 수 있다(Fig. 5). 또한, Fig. 6에 나타난 바와 같이 지표면 침하량은 모형지반 중심, 즉 공동 중심 상부에서 최대값이 발생되고, 중심부에서 멀어질수록 그 값이 감소하고 있음을 알 수 있으며, 이러한 현상은 공동 직경이 클수록 더욱 현저하게 나타나고 있다. 한편, 교통하중의 적용에 따른 모형지반의 전단응력은 공동 양 측면으로 증가하고 있으며 공동 직경이 증가할수록 증가 범위가 확장됨을 알 수 있다(Fig. 7).
4. 포장층 두께와 교통하중의 크기를 고려한 지반 안전율 분석
4.1 응력비 분포와 지반 안전율 상관관계 분석
4.1.1 응력비(SR)와 안전율 정의
일반적으로 지반은 상재하중에 의한 압축력이 작용하게 되면 소정의 파괴면에서 전단응력과 전단변형률이 발생하게 되며 재료적 파괴 시점에서 한계전단응력 값인 전단강도를 나타내게 된다. 즉, 지반의 전단강도는 파괴상태의 pf와 qf값의 상관관계로부터 생성되는 Kf-line 상에서 식 (9)와 같이 표현할 수 있다.
본 논문에서는 지반의 한 요소에 대한 전단강도와 재하로 인해 발생 된 전단응력 값의 비를 응력비(SR: Stress Ratio)로 정의함으로써, 공동 생성에 의한 응력해방 및 교통하중 재하로 인한 응력 변화 양상, 지반의 파괴상태 도달 정도를 분석할 수 있도록 하였다. 응력비는 식 (10)과 같이 나타낼 수 있으며, 이는 지반조건 및 하중조건에 따른 지반의 파괴상태를 판단하는데 중요한 지표라 할 수 있다. 한편, 하중 재하에 따른 해석지반의 안정성을 분석하기 위하여 식 (11)과 같이 응력비를 이용한 안전율(F.S)을 정의하였다. 즉, 해석 조건에 따른 지반의 전반적인 안정성을 정량적으로 평가하기 위하여 응력비와 역수관계인 안전율의 분포를 분석함으로써, 포장층 두께와 교통하중 크기의 변화가 지중공동 주변지반의 안정성에 미치는 영향을 분석하였다.
| $$\tau_\max=\frac{\sigma_1+\sigma_3}2sin\varphi+ccos\varphi$$ | (9) |
| $$SR=\frac{\tau_{mob}}{\tau_\max}$$ | (10) |
| $$F.S=\frac{\tau_\max}{\tau_{mob}}$$ | (11) |
4.1.2 응력비 분포 특성
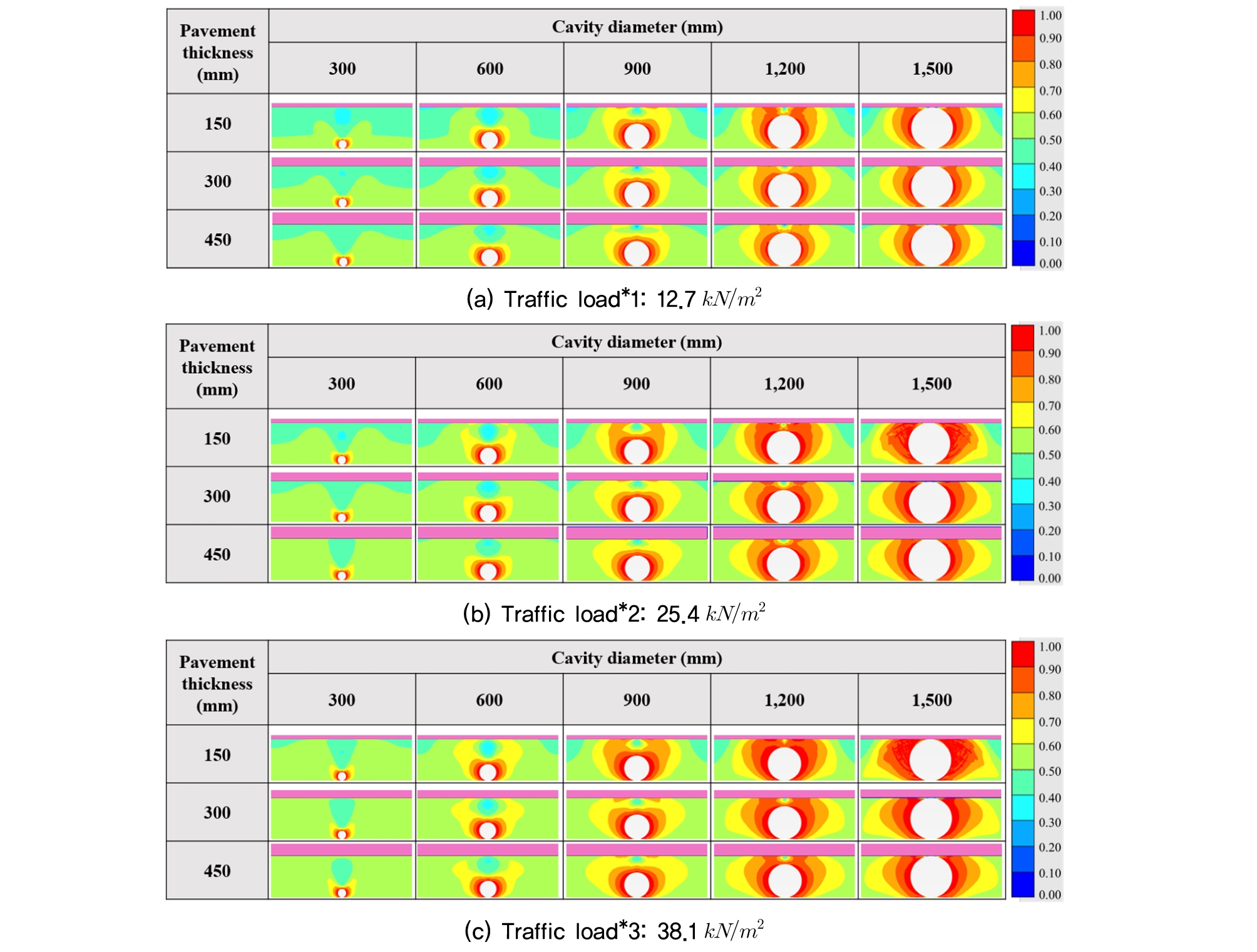
Fig. 8은 대표적인 응력비 분포도를 나타낸 결과로써, 매립심도가 1,500mm일 때, 공동직경 및 포장층 두께에 따라 교통하중 조건별로 도식화하였다. 그림에서 보는 바와 같이, 공동과 인접한 지반에서는 응력비가 1로 표현되는 영역이 형성됨을 확인하였다. 특히, 교통하중이 증가함에 따라 포장층 두께가 감소하고 공동 직경이 증가할수록, 전단응력이 전단강도에 도달하는 영역을 더욱 뚜렷하게 확인할 수 있었다. 한편, 공동 직경이 1,200mm 이상의 조건에서는 교통하중의 크기와 관계없이 포장층에 근접한 지반의 응력비가 1에 가까워지는 것을 알 수 있었고, 이와 같은 경향은 포장층의 두께가 감소할수록 그 범위가 증가하는 것으로 나타났다. 이는 공동 직경의 증가 및 포장층 두께의 감소로 인하여 지반의 안정성이 상대적으로 감소되는 것을 의미한다. 따라서 응력비를 이용하여 공동이 발생된 지반의 다양한 조건(하중, 포장층 두께, 공동 크기)에 따른 지반의 안정성 검토가 가능한 것으로 판단된다.
4.1.3 안전율 분포 특성
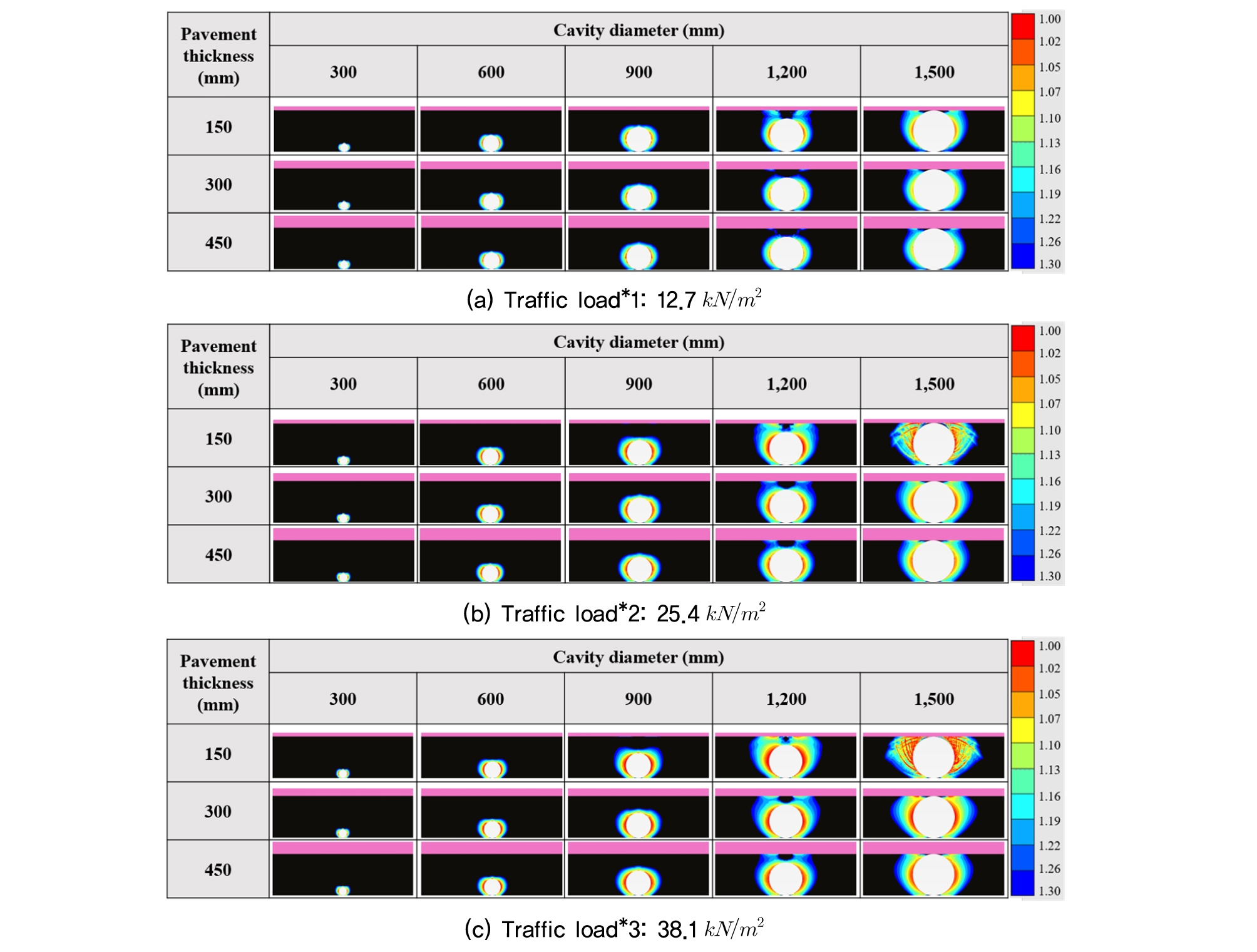
응력비 분포 특성을 분석한 경우와 마찬가지로, 매립심도가 1,500mm일 때의 해석결과를 바탕으로 응력비의 역수관계인 안전율을 이용한 분포도를 Fig. 9에 나타내었다. 이때, 기준안전율은 굴착지반의 허용안전율(F.S=1.3)을 적용하였으며, 그림에서는 허용안전율 미만의 영역이 표시되도록 하였다. 그 결과, 공동 직경이 900mm 이하인 경우, 포장층 두께가 감소할수록 허용안전율 미만의 범위는 수평방향으로 확장되는 양상을 보였다. 그러나 공동 직경이 1,200mm 이상부터는 수직방향으로도 안전율이 감소함으로써 그 범위가 지표면까지 확장되었다. 즉, 허용안전율보다 작은 안전율의 범위는 교통하중 증가와 포장층 두께 감소에 따라 확장되는 것을 확인하였다. 이와 같은 안전율 분포는 응력비 분포 양상과 동일한 특성을 나타낸 결과로써, 이를 바탕으로 공동 주변 지반의 전단응력 발생 특성을 고려한 안전율을 통해 공동 발생 지반의 안정성 평가가 가능한 것으로 판단된다.
4.2 지표침하량과 공동직경의 상관관계 분석
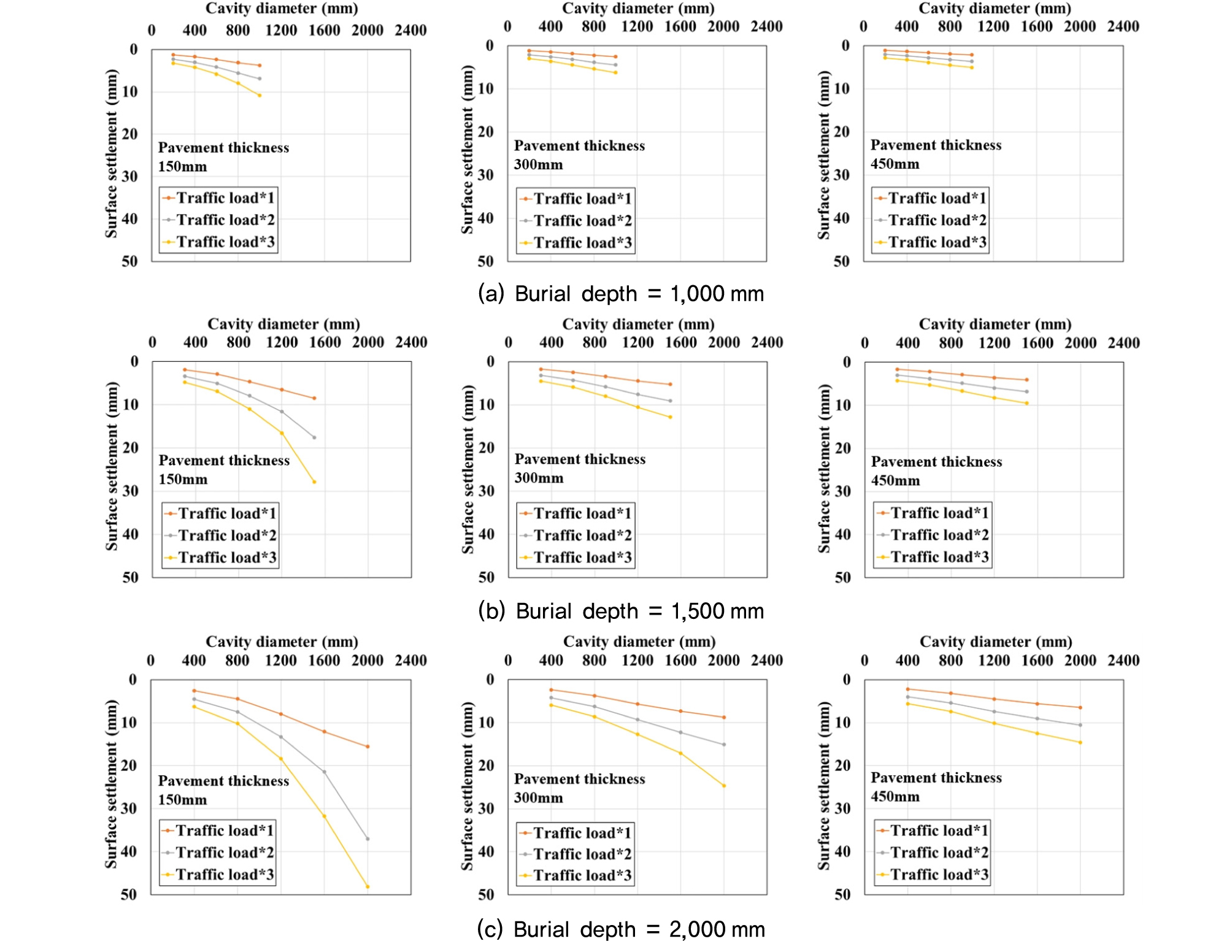
전술한 내용을 바탕으로, 지표침하량과 공동직경의 상관관계를 분석하기 위하여, Fig. 10과 같이 교통하중에 따른 지표침하량과 공동직경의 관계를 포장층 두께별로 매립심도에 따라 나타내었다.
먼저, 각 매립심도 조건에서 동일한 교통하중이 작용할 때, 포장층의 두께가 증가할수록 공동직경에 따른 지표침하량의 기울기가 완만해지는 것을 확인하였다. 즉, 공동직경이 동일한 경우라도 포장층의 두께가 증가하면 지표침하량이 감소하였다. 또한 동일한 포장층 두께의 조건에서 교통하중의 크기와 공동직경이 증가할수록 지표침하량은 증가하였으며, 이와 같은 경향은 매립심도가 증가할수록 확연히 나타나는 것으로 분석되었다. 따라서 매립심도, 교통하중, 포장층 두께 및 공동직경이 지표침하 발생의 영향요소임을 확인하였으며, 본 절에서 나타낸 상관관계를 바탕으로 지표침하량을 이용하여 공동직경의 예측이 가능할 것으로 판단된다.
4.3 지표침하량과 비파괴심도의 상관관계 분석
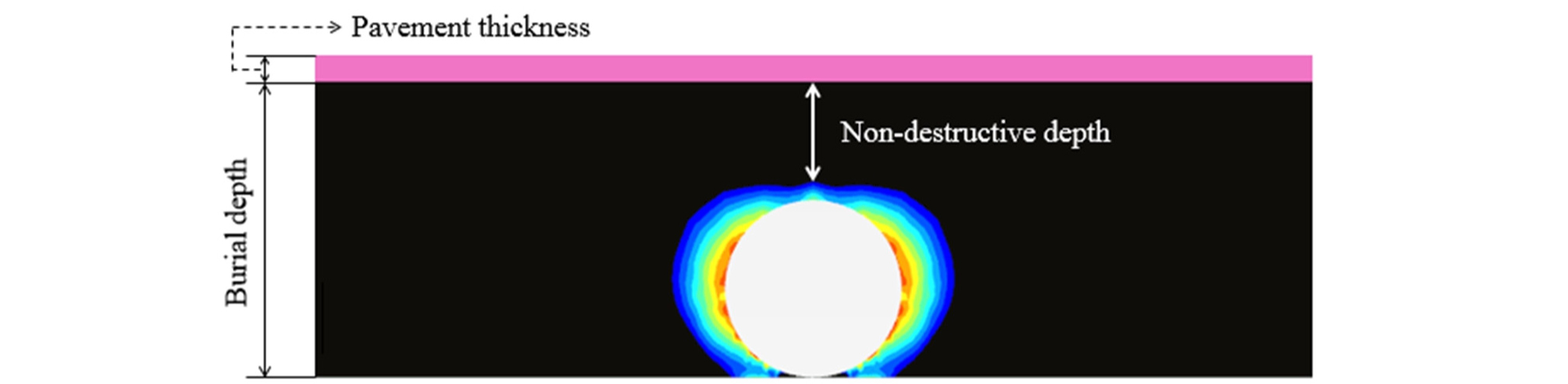
안전율 분포도를 이용하여 공동이 발생된 지반의 비파괴심도를 파악하고자, Fig. 11에 나타낸 바와 같이, 공동 상부 지반의 허용안전율(F.S.=1.3) 이상의 경계에서부터 포장층 하부 지반까지의 높이를 비파괴심도로 정의하였다.
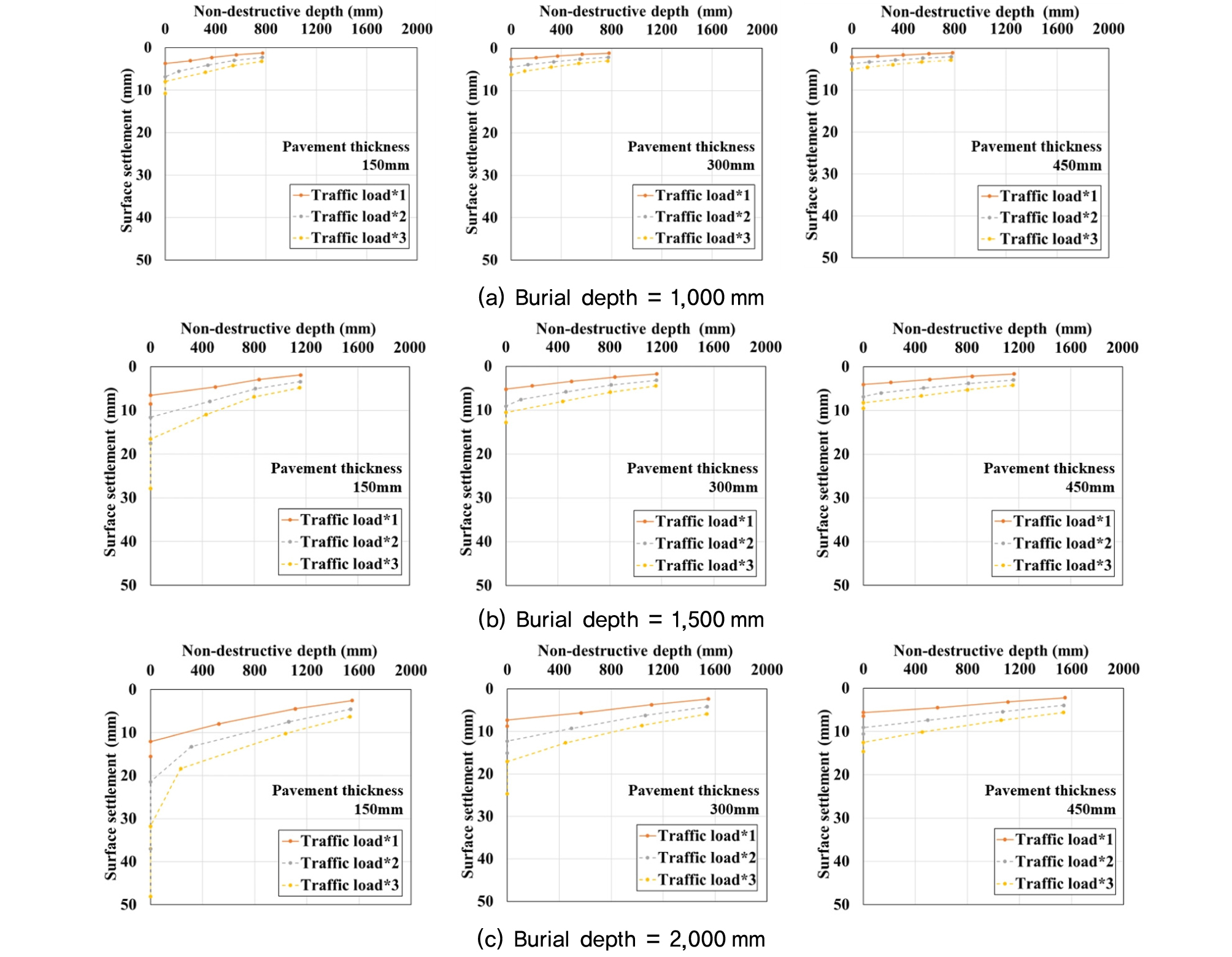
Fig. 12는 교통하중에 따른 지표침하량과 비파괴심도의 관계를 포장층 두께별로 매립심도에 따라 도식화한 것이다. 안전율 분포도를 이용한 비파괴심도의 크기를 분석한 결과, 공동직경 및 교통하중 크기가 작고 포장층 두께가 클수록 비파괴심도는 증가하였다. 이와 같은 비파괴심도 분포 특성을 통해 지표침하량과의 관계를 분석한 결과, 모든 매립심도 조건에서 비파괴심도가 클수록 지표침하량은 감소하는 경향을 나타냈다. 즉, 각 매립심도의 약 60% 이하 크기의 직경을 갖는 공동이 발생된 경우, 비파괴심도는 교통하중 및 포장층 조건에 따라 변화하지만, 허용안전율 이하의 영역이 지표면까지 미치지 않기 때문에, 지표침하량은 감소하였다. 그러나 각 매립심도의 약 80% 이상 크기의 공동이 발생하면 허용안전율 미만의 영역이 지표면까지 영향을 미치기 때문에, 비파괴심도가 0에 가까워짐에 따라 지표침하량이 크게 증가하는 것으로 분석되었다. 이러한 상관관계를 바탕으로 지표침하량을 통해 비파괴심도를 예측함으로써 지반의 안정성 파악이 가능할 것으로 판단된다.
4.4 비파괴심도와 공동직경의 상관관계 분석
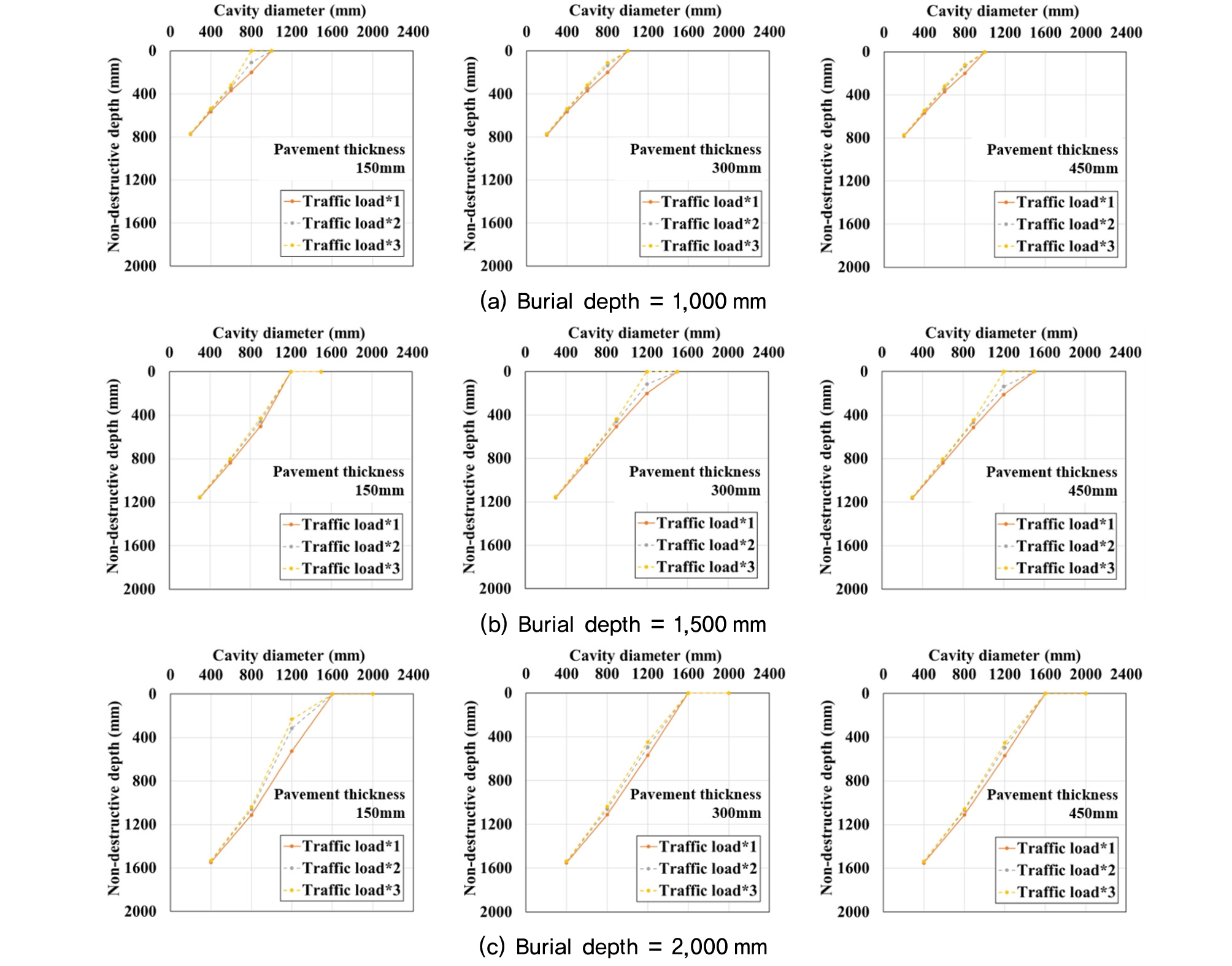
Fig. 13은 공동직경과 비파괴심도의 관계를 나타낸 것이다. 모든 해석종류에 있어서 공동 직경이 클수록 비파괴심도는 감소하는 경향으로 나타났으며, 각 매립심도 조건에서 약 80% 이상 크기의 공동이 발생하면 허용안전율 미만의 영역이 지표까지 확장됨에 따라 비파괴심도는 0에 가까워진다. 이는 매립심도의 약 80% 정도 직경을 갖는 공동이 발생하게 되면, 공동에 의해 지표면까지 전단강도가 감소함으로써 지반의 안정성이 낮아짐을 의미하는 결과이다. 한편, 포장층 두께가 동일한 경우에는 교통하중의 크기가 공동직경에 따른 비파괴심도에 미치는 영향은 거의 없는 것으로 분석되었다.
5. 결 론
본 연구에서는 공동 발생 지반의 안전성 분석을 위해 포장층 두께와 교통하중 크기의 변화를 고려한 유한요소 수치해석을 수행하였다. 매립심도, 공동직경을 고려하여 다양한 공동 발생 지반을 모사하였으며, 수치해석 결과를 바탕으로 응력비 및 안전율과 지표침하량 그리고 비파괴심도를 이용하여 지반의 전반적인 안정성을 판단하였다. 그 결과를 정리하면 다음과 같다.
(1) 응력비 분포를 분석한 결과, 응력비(SR)가 1로 표현되는 영역은 공동과 인접한 지반에서 형성되었고, 교통하중이 증가함에 따라 포장층 두께가 감소하고 공동직경이 증가할수록 전단응력이 전단강도에 도달하는 영역이 확장됨을 확인함으로써 지반의 안정성이 상대적으로 감소되는 것을 확인할 수 있었다. 이러한 결과로, 응력비를 통해 지반의 안정성 검토가 가능한 것으로 판단된다.
(2) 안전율 분포를 분석한 결과, 허용안전율(F.S: 1.3)의 경계를 확인할 수 있었으며, 허용안전율 미만의 영역을 통해 각 지반요소들의 안전율 변화를 확인할 수 있었다. 그 결과, 응력비 분포의 경향과 유사하게 하중의 증가, 포장층 두께의 감소, 공동직경의 증가로 인한 지반의 안정성 감소를 확인하였다. 따라서, 안전율 분포를 통해 지반의 안정성 평가가 가능한 것으로 판단된다.
(3) 지표침하량과 공동 직경의 상관관계를 분석한 결과, 각 매립심도 조건에서 공동직경이 동일하더라도 포장층 두께가 증가할수록 지표침하량은 감소함을 확인할 수 있었으며 또한, 동일한 포장층 두께의 조건에서는 교통하중의 크기와 공동직경이 증가할수록 지표침하량은 증가하였고 이러한 경향은매립심도가 증가할수록 뚜렷하게 나타났다. 이러한 상관관계를 바탕으로 지표침하량을 통해 공동직경의 예측이 가능할 것으로 판단된다.
(4) 비파괴심도는 공동직경 및 교통하중 크기가 작고 포장층 두께가 클수록 증가한다. 이러한 결과를 바탕으로 지표침하량과 비파괴심도의 상관관계를 분석한 결과, 모든 매립심도 조건에서 비파괴심도가 클수록 지표침하량은 감소하는 경향을 확인할 수 있었다. 따라서 지표침하량을 통해 비파괴심도를 예측하여 지반의 안정성 파악이 가능할 것으로 판단된다.
(5) 비파괴심도와 공동 직경의 상관관계를 분석한 결과, 공동직경이 클수록 비파괴심도는 감소하는 경향을 확인할 수 있었으며, 각 매립심도의 80% 정도 직경을 갖는 공동이 발생하면, 공동에 의해 전단강도가 지표면까지 감소하여 비파괴심도가 0에 도달하는 것을 확인함으로써 지반의 안정성의 감소를 확인할 수 있었다. 따라서, 비파괴심도와 공동직경의 상관관계를 통하여 지반의 안정성 평가가 가능할 것으로 판단된다.