1. 서 론

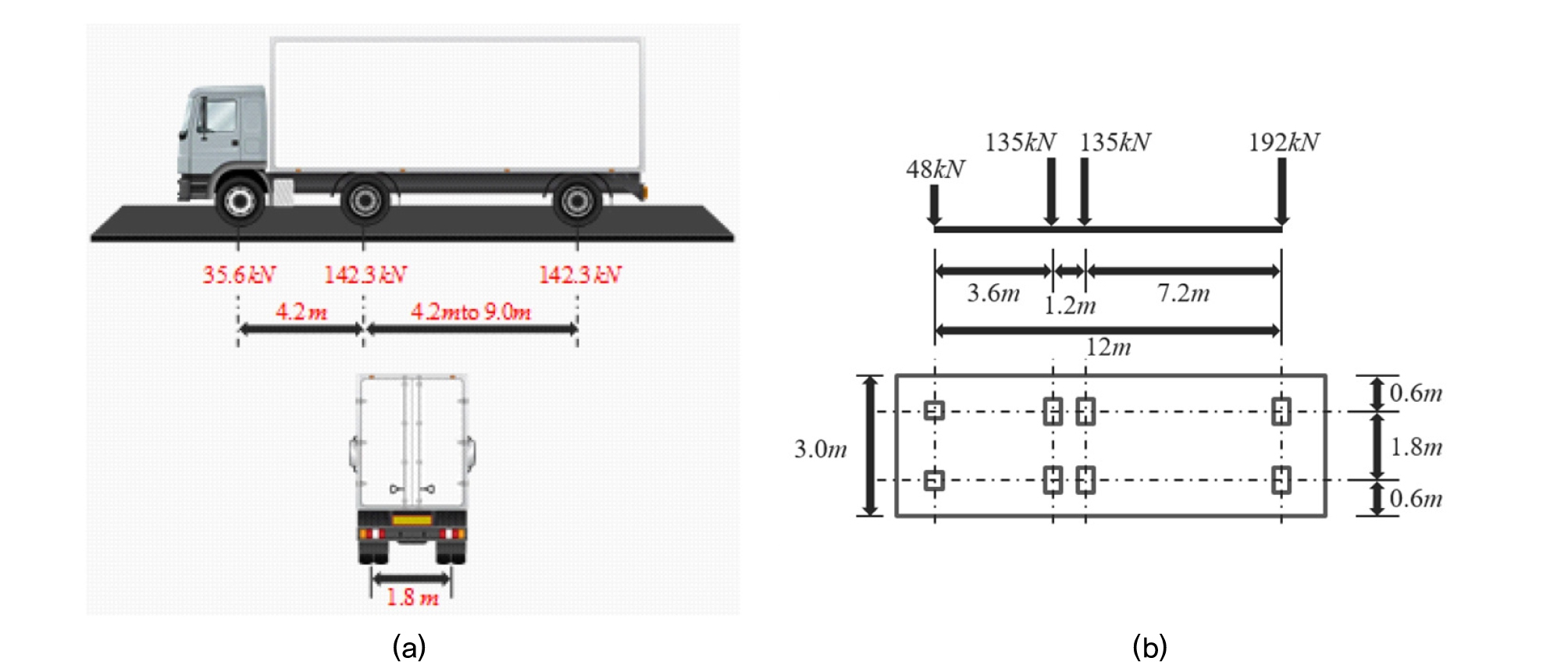
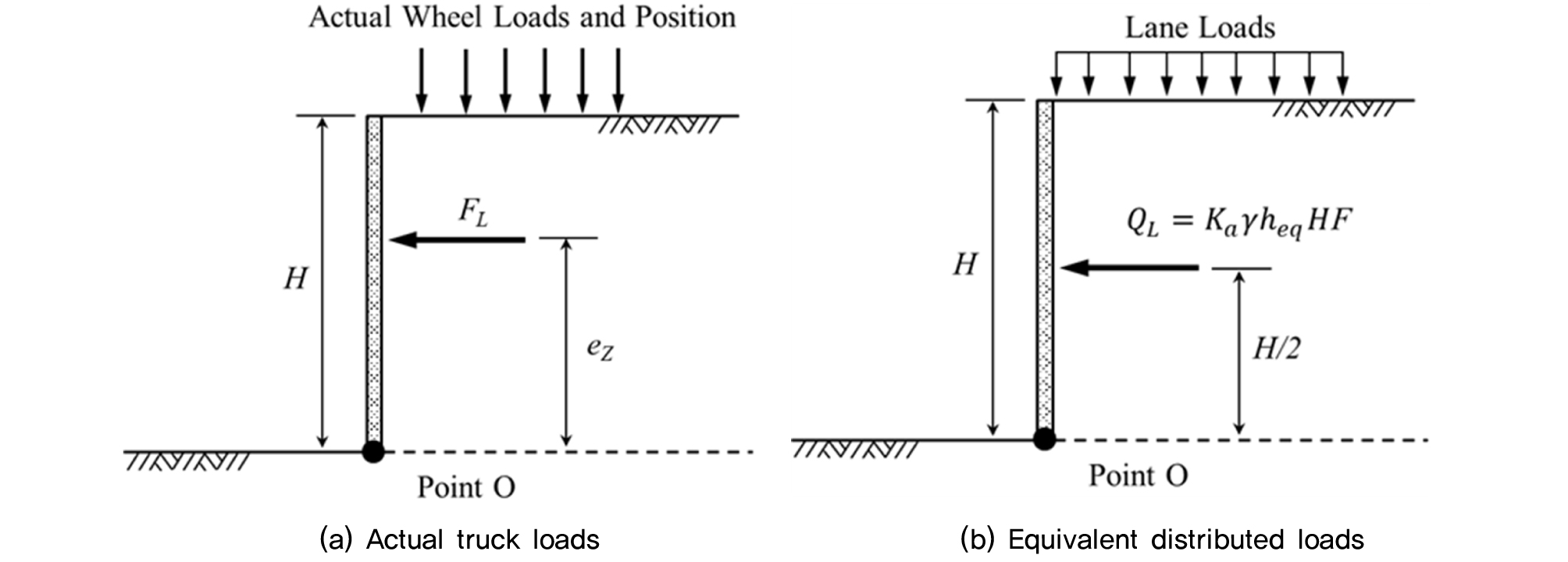
도로교 한계상태설계법은 2015년부터 시행하는 국내 도로교 설계에 적용되고 있지만, 도로교 한계상태설계법(토압편)에서는 국내트럭하중조건을 고려한 토압하중계수(등가상재하중높이) 제시되지 않아 설계에 적용하는데 많은 어려움이 있다. 미국 AASHTO 한계상태설계법(2012)에서는 옹벽배면에 표준트럭 하중을 적용하여 옹벽에 발생하는 수평토압을 이론적으로 산정한 후 토압하중계수를 제시하고 있다. 여기서 토압하중계수란 표준트럭 축하중에 의해 옹벽에 발생되는 수평토압을 배면토사의 단위중량으로 나눈 값이며, 이후 “등가상재하중 높이”로 정의한다. 하지만 Fig. 1과 같이 미국 표준트럭하중의 축하중 크기와 위치, 차선하중(lane load)의 크기 등이 우리나라 표준트럭하중 특성과 다르기 때문에 미국 AASHTO에서 제시된 등가상재하중 높이(h_eq)를 국내 도로설계기준으로 준용하기가 곤란한 실정이다(MOCT, 2003a; MOCT, 2003b; MLTMA, 2012).

Fig. 1.

Design truck loads: (a) AASHTO (2012), (b) MOLIT (2016a)

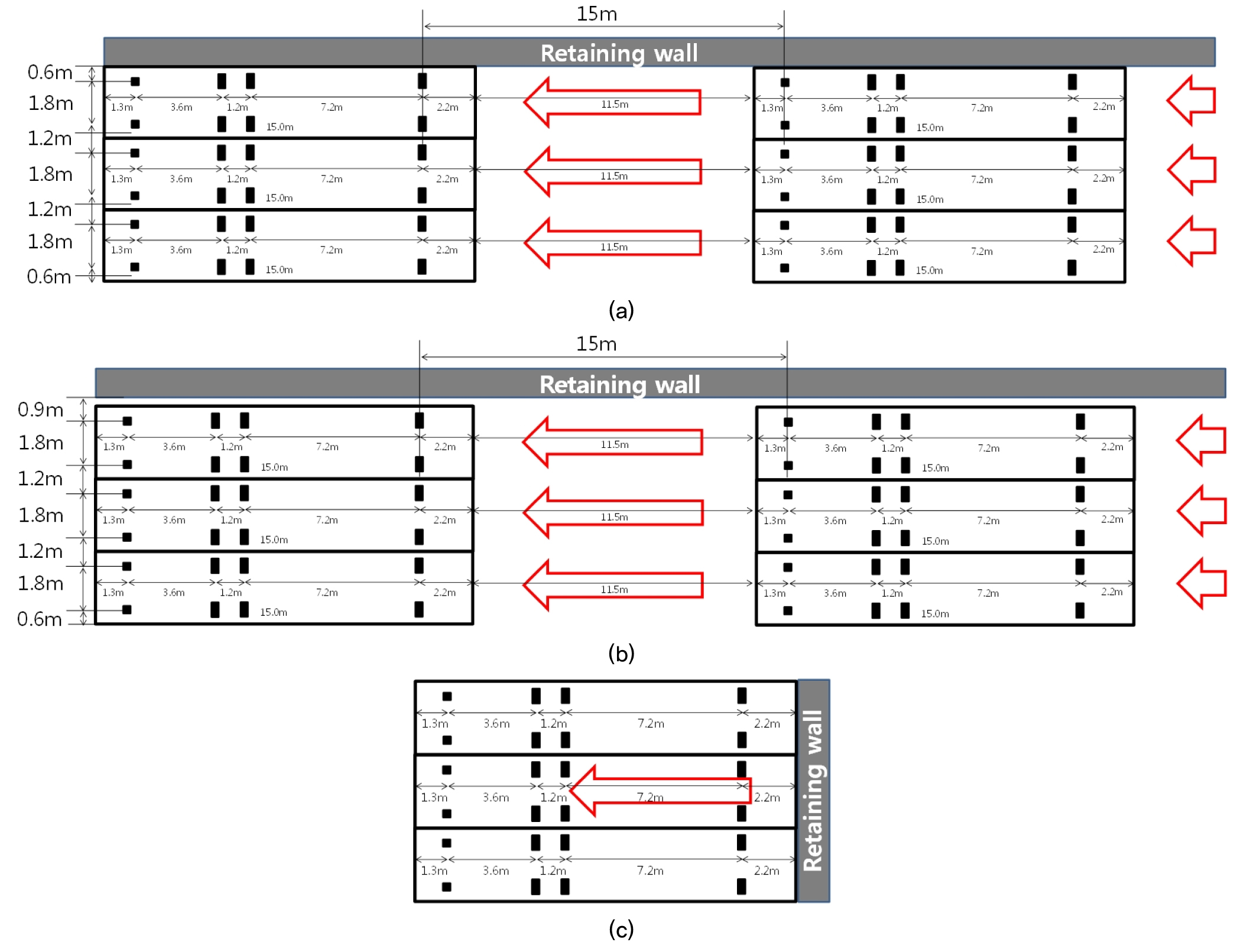
트럭하중에 의해 옹벽에 유발되는 수평토압 특성은 수평토압 합력의 크기와 수평토압 합력의 작용위치를 포함하고 있다. 수평토압 합력은 옹벽의 수평활동(Sliding) 안정성 검토에 필요하고, 수평토압 합력과 작용위치는 옹벽의 전도(Overturning) 안정성 검토에 필요하다. 이러한 안정성 검토를 통해 국내트럭하중조건을 반영한 등가상재하중 높이(h_eq) 제안이 필요하다. AASHTO LRFD Bridge Design Specifications(2012)에서는 옹벽의 벽체를 Non-yielding wall로 가정하여 Boussinesq 이론식으로 계산하여 옹벽높이별(H=1.5m, 3.0m, 6.0m) 등가상재하중높이(h_eq)를 제안하고 있다. 또한 국내 기준에 따르면 ‘우리나라 차량 축하중 100%’를 반영한 h_eq와 ‘우리나라 차량 축하중 75%와 차선하중(lane load = 4.233kPa)’를 반영한 h_eq를 모두 산정하여 보수적인 값을 제시하도록 되어 있다(MOLIT, 2016a; MOLIT, 2016b). 따라서 본 연구에서는 국내 표준트럭의 축하중 위치, 크기, 옹벽과 트럭 배치 특성(Fig. 2)을 반영하여 3차원 수치해석적 방법으로 옹벽높이별 등가상재하중 높이를 제안하고자 한다.

2. 국내 표준트럭하중 특성을 반영한 등가상재하중 높이 결정방법

2.1 옹벽배면 국내 표준트럭하중 조건

Fig. 1(b)는 국내 표준트럭 1대의 차량하중 크기와 위치, 배치 평면도를 나타낸다. 각 차량이 차지하는 평면적은 3m(폭)×15.5m(길이)이며, 차량당 4개 차축(8개 차륜)을 통해 하중이 지표로 전달된다. Lee et al.(2017)은 수치해석을 통해 도로의 차선 수, 차량 하중의 크기 및 옹벽으로부터 떨어진 거리에 따라 옹벽에 가해지는 수평토압을 분석하였으며, 차량하중 이격거리가 옹벽 높이보다 클 경우 수평토압의 변화는 미미하였다. 이러한 점을 고려하여 본 연구에서 국내 표준트럭이 옹벽에 배치되는 위치와 방향은 Fig. 2(a)~(c)와 같다. Fig. 2에서 (a)는 옹벽의 방향과 차량 진행방향이 평행하고 차량과 옹벽의 이격거리가 0.0m이며, (b)는 동일한 조건에 차량과 옹벽의 이격거리가 0.3m이다. Fig. 2(c)는 옹벽의 방향과 차량 진행방향이 직교하는 경우이며, 옹벽과의 차량과 옹벽의 이격거리가 0.0m인 경우를 나타낸다. 여기서, 각 트럭이 차지하는 평면적에 등분포하중(lane load) 4.233kPa를 추가 반영하였다.

Fig. 2.

Configuration of truck loads: (a) trucks parallel and adjacent to the wall, (b) trucks parallel to the wall with a distance of 0.3m, (c) trucks perpendicular to the wall (plan view)

2.2 국내 표준트럭하중이 옹벽에 가해지는 수평토압의 합력 및 작용점 산정방법

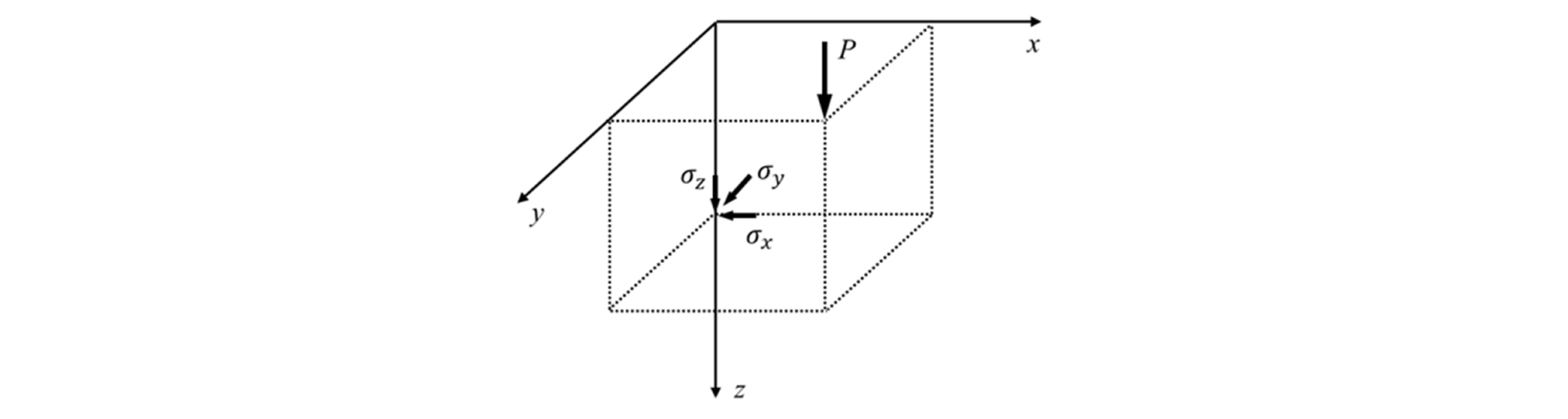
옹벽과 트럭 배치 특성과 옹벽높이(H=1.5m, 3.0m, 6.0m)에 따른 등가상재하중 높이(h_eq)를 산정하기 위해 옹벽에 작용하는 수평토압의 합력 및 작용점 계산이 필요하다. 반무한 탄성체 표면에 작용하는 연직 및 수평 절점하중에 의한 토압은 Boussinesq 이론으로 계산할 수 있으며, 옹벽의 뒷채움 토사는 탄성체로 가정하고 지반은 균질하고 등방성 매체로 가정한다(Lee, 2016). Fig. 3과 같은 좌표계에서 옹벽면이 y축과 z축이 이루는 면으로 가정하면, x-y축의 상부 한 점에 하중 P가 지표면에 연직으로 작용하는 경우 옹벽면에 작용하는 수평력 σ_x는 식 (1)을 이용하여 구할 수 있다.

Fig. 3.

Point load(P) on surface in cartesian coordinates

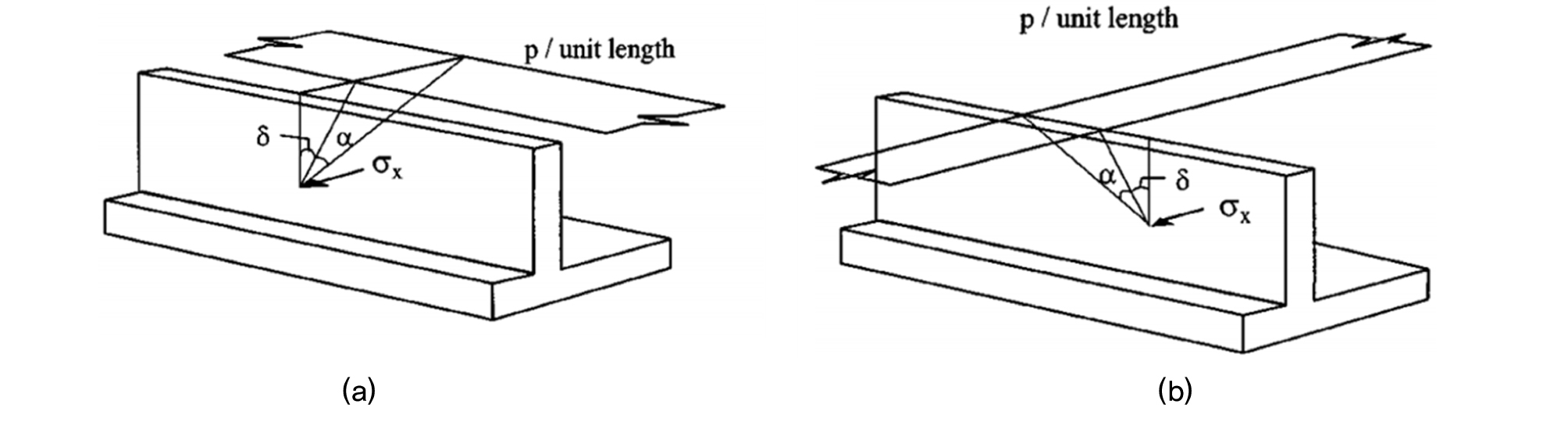
여기서, $R=\sqrt{x^2+y^2+z^2}=\sqrt{r^2+z^2}$, $r=\sqrt{x^2+y^2}$, ν는 포아송 비이다. Holl(1940)과 Poulos and Davis(1974)는 옹벽 배면 상단의 교통하중을 폭과 길이를 가진 띠하중으로 표현하고 이 하중에 옹벽과 평행하거나 직교할 때 옹벽 배면에 가해지는 압력 σ_x를 구하였다. 교통하중을 산정할 때 작용한 무한 등분포 차선하중(lane load)을 고려하기 위해서는 옹벽방향과 차량진행방향의 조건에 따라 식 (1)은 식 (2), (3)으로 나타낼 수 있다(Kim and Barker, 2002). 식 (2)는 옹벽이 길이방향과 차량의 진행방향이 평행한 조건에서 차선하중이 벽체의 위치에 따라 작용하는 응력을 나타낸다(Fig. 4(a)).

Fig. 4.

Earth pressure induced by truck load and lane loads acting: (a) parallel to the wall and (b) perpendicular to the wall (Kim and Barker, 2002)

식 (3)은 옹벽의 길이방향과 차량의 진행방향이 직교하는 조건에서 차선하중이 벽체의 위치에 따라 작용하는 응력을 나타낸다(Fig. 4(b)).

식 (4)는 수평토압합력(F_L)을 산정하기 위해 옹벽에 작용하는 수평토압의 면적을 적분하여 구하는 과정을 나타낸다. 여기서, F_L, H, σ_x는 각각 전달되는 수평토압의 합력(total lateral pressure), 옹벽 높이, 임의의 높이(z)에서 옹벽에 전달되는 수평토압을 나타낸다.

수평합력 작용점은 옹벽 하단면에 대해서 모멘트 평형 방정식을 이용하여 식 (5)와 같이 구할 수 있다. 여기서, e_z, z는 옹벽 바닥면 기준 수평합력 작용점(높이)과 옹벽의 임의 지점 높이를 각각 나타낸다.

2.3 국내 표준트럭하중과 동일한 등가상재하중 높이 h_eq 산정방법

실제 상재 차량하중(actual wheel loads) 및 등가등분포하중(equivalent distributed loads) 재하 시 전달되는 수평합력 크기 및 작용점 위치는 Fig. 5와 같다.

Fig. 5.

Calculation of total lateral pressure against retaining wall and its elevation

실제 상재 차량하중에 의해 옹벽에 추가 전달되는 합력과 등가상재하중에 의한 합력은 같으므로, $\sum F_{L_i}=K_a\gamma h_{eq}H$로 나타낼 수 있다. 즉, 등가수평력 방법에 의해 계산된 높이 h_eq는 식 (6)과 같이 계산할 수 있다.

실제 차량하중에 의한 모멘트와 등가상재하중을 고려한 모멘트는 F_Le_z = Q_L H/2이므로 $\sum F_{L_i}{e}_z=K_a\gamma h_{eq}{H}^2/2$가 된다. 즉, 등가모멘트 방법에 의한 h_eq는 식 (7)로부터 산정할 수 있다.

본 연구에서는 국내 표준트럭의 축하중 위치, 크기, 옹벽과 트럭 배치 특성을 반영하여 3차원 수치해석을 통해 옹벽높이별 등가상재하중 높이(h_eq)를 산정하였다. 옹벽과 트럭하중 배치 조건은 Fig. 2와 같이 총 3가지 Case로 적용하였으며, 옹벽높이는 H=1.5m, 3.0m, 6.0m를 적용하였다.

3. 수치해석에 의한 등가상재하중 높이(h_eq) 산정

3.1 유한요소해석 개요

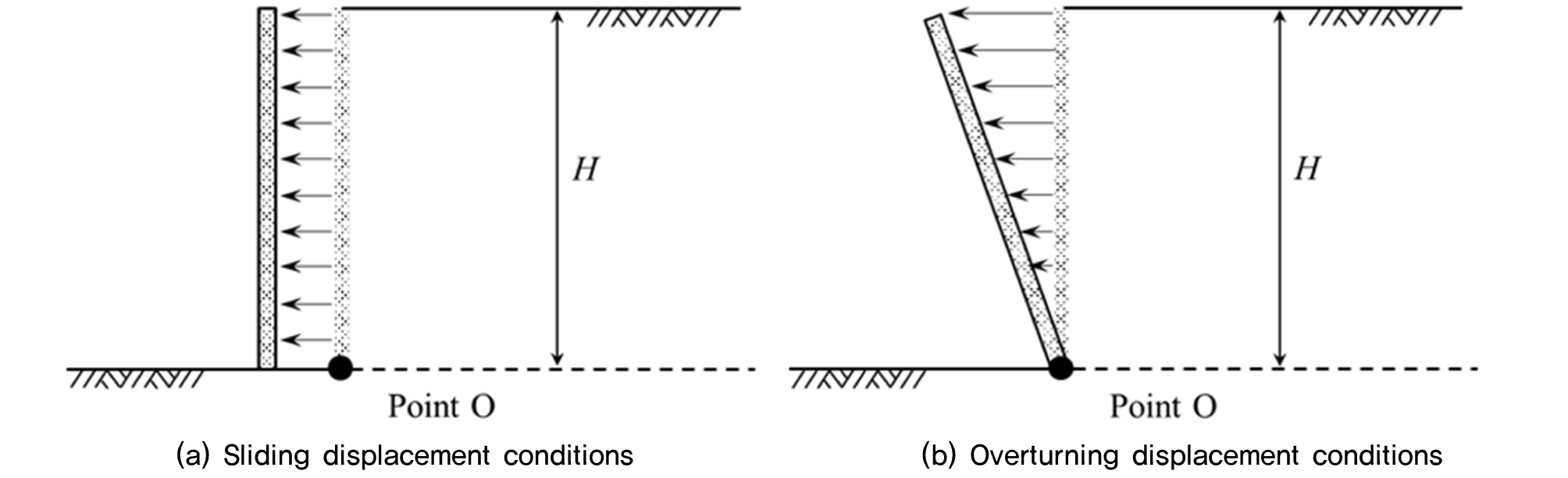
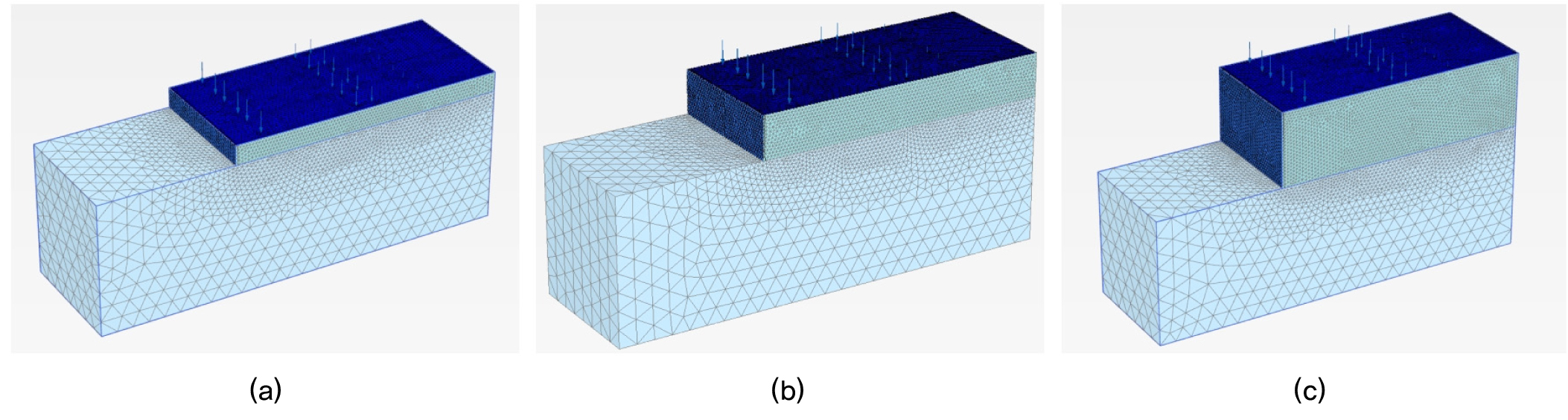
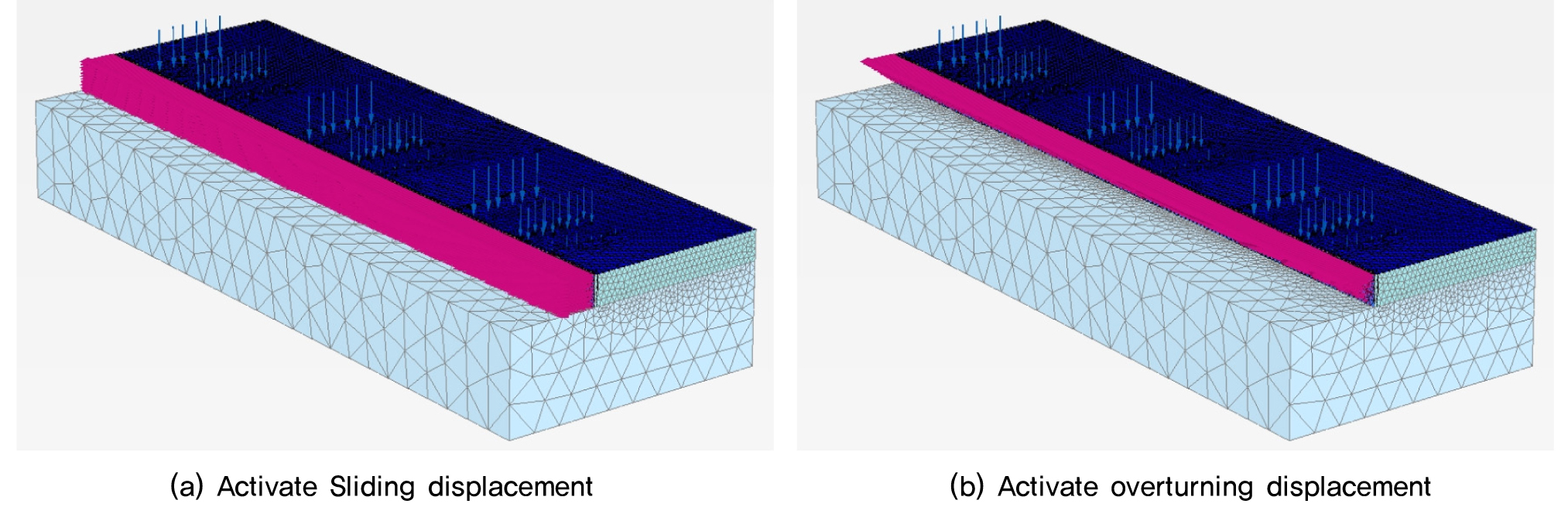
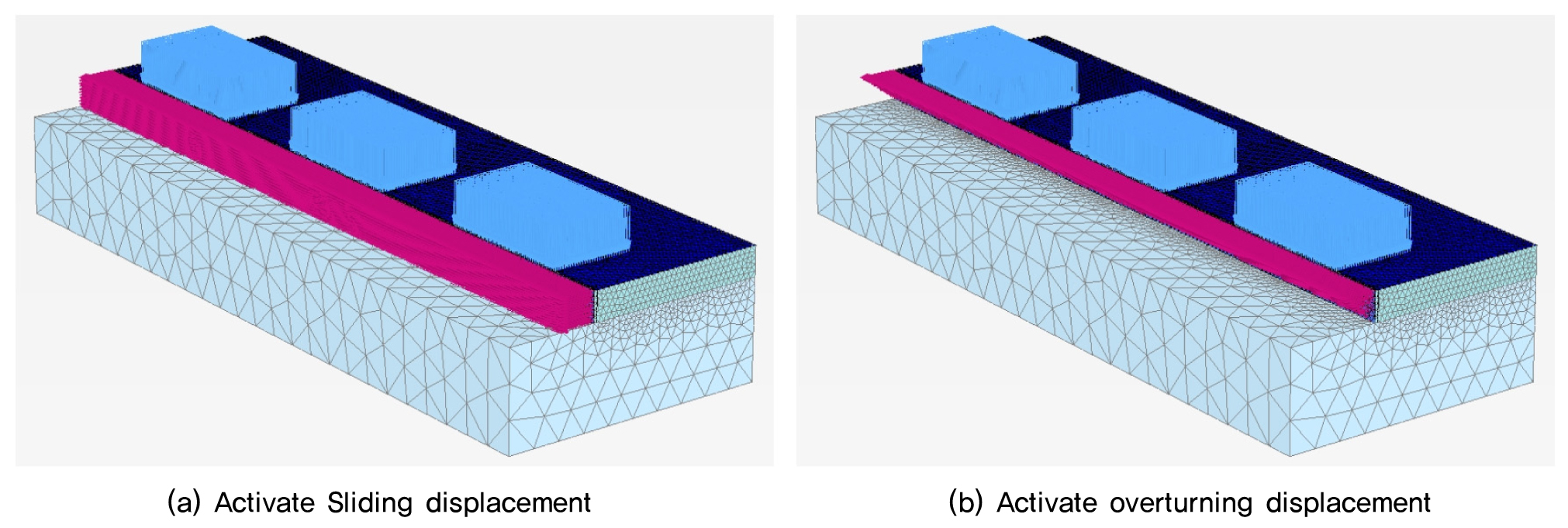
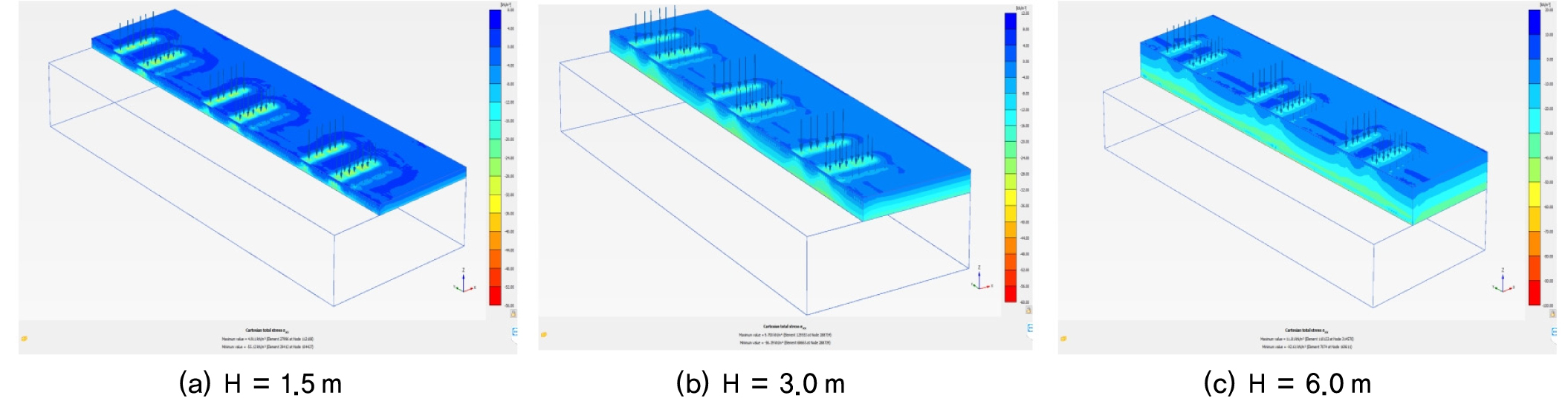
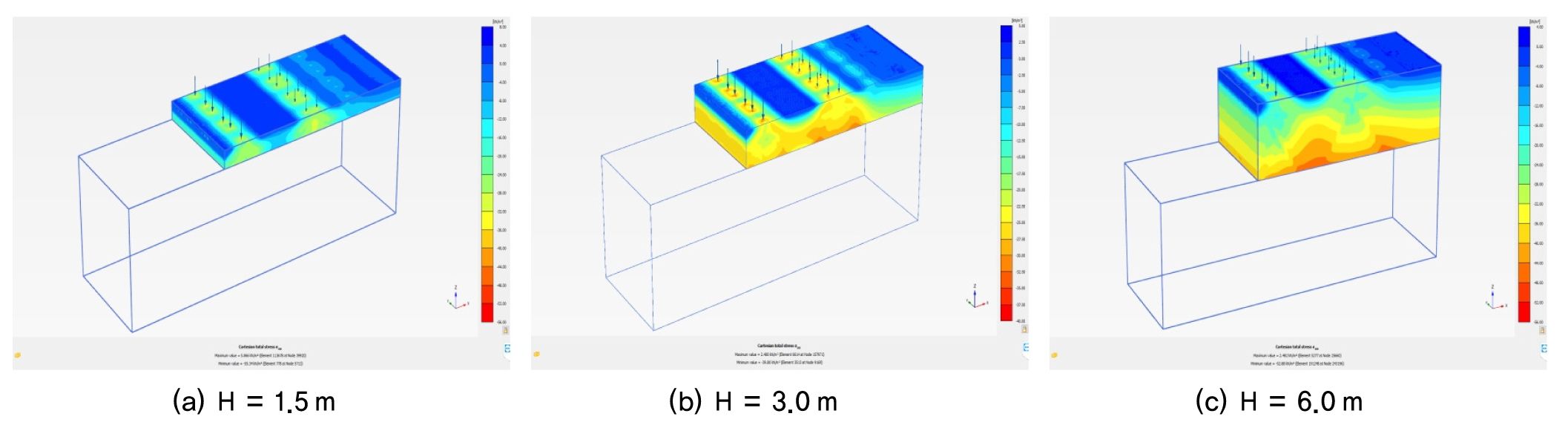
수치해석은 PLAXIS사의 Plaxis3D(Plaxis VB, 2017)를 사용하였으며, 국내 표준트럭하중배치(Case 1, Case 2, Case 3), 옹벽높이(H=1.5m, 3.0m, 6.0m), 옹벽 배면하중(축하중 100%, 축하중75%+차선하중 4.233kN/m²), 옹벽변위(활동변위조건, 전도변위조건) 조건에 따라 등가상재하중 높이를 산정하였다. 3차원 수치해석에 의한 유한요소 해석종류는 Table 1과 같다. 수평토압으로 인해 옹벽에 주동변위가 발생하고 이로 인해 옹벽배면 지반의 팽창파괴 시 토압을 주동토압이라 한다. 따라서 Fig. 6과 같이 국내 표준트럭 하중을 적용한 후 옹벽에 변위(활동 및 전도 변위)를 점차 증가시켜 변위에 따른 주동토압과 등가상재하중 높이를 산정하고자 한다. 이는 주동변위 증가 및 배면지반의 팽창파괴로 인해 발생하는 토압에 대하여 등가상재하중 높이를 산정하기 위함이다.

Table 1. 3D finite element analysis type

Fig. 6.

Displacement conditions of retaining wall

3.2 해석방법 및 내용

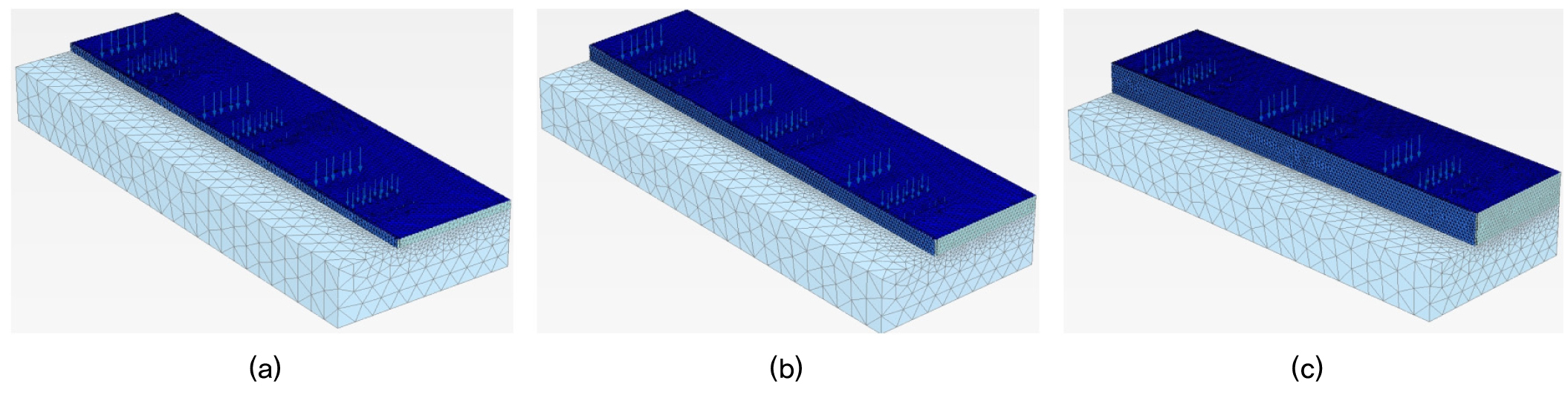
국내 표준트럭의 축하중 위치, 크기, 옹벽과 트럭 배치 특성을 반영한 3차원 유한요소망(finite element mesh)은 Fig. 7∼9에 나타낸 바와 같다. 기초지반, 배면토사에는 15절점 삼각형요소와 Mohr Coulomb 모델을 적용하였으며, 중력식옹벽과 포장층은 5절점 plate 요소와 선형탄성(Linear-Elastic)모델을 사용하였다. 그리고 옹벽-배면토 경계는 12절점 요소와 인터페이스(interface)로 모델링하였다. 3차원 유한요소망에서 X방향 및 Y방향은 수평변위를 구속하였으며, 유한요소망 Z방향 최저면은 연직변위를 구속하였다. 그리고 구속조건(boundary condition)이 해석 결과에 영향을 주지 않도록 옹벽을 기준으로 충분한 수평 및 연직 거리를 적용하였다. 3차원 유한요소망에 이용된 요소수 및 절점수는 검토영향요소(축하중 위치, 크기, 옹벽높이, 트럭하중배치조건)에 따라 차등 적용하였으며, 요소수는 147,758∼464,365개, 절점수는 213,148∼644,950개로 모델링 하였다.

Fig. 7.

Finite element mesh in Case 1; (a) H=1.5m, (b) H=3.0m, (c) H=6.0m

Fig. 8.

Finite element mesh in Case 2; (a) H=1.5m, (b) H=3.0m, (c) H=6.0m

Fig. 9.

Finite element mesh in Case 3; (a) H=1.5m, (b) H=3.0m, (c) H=6.0m

3.3 수치해석 Parameter

수치해석에 적용한 기초지반, 및 뒤채움 토사의 물성치를 Table 2에, 포장층 및 옹벽의 물성치는 Table 3에 나타내었다. 옹벽은 중력식 옹벽으로서 철근이 배근되지 않은 무근콘크리트로 가정하였으며, 식 (8)에 의해 재료의 탄성계수를 산정하였다(MLTMA, 2012). 이때, 적용한 콘트리트의 단위중량은 2,350kg/m³이며, 극한 압축강도(f_u)는 재령 28일에서의 콘크리트의 평균압축강도로 f_ck+Δf와 같다. 여기서, +Δf는 f_ck가 40MPa 이하일 경우 4MPa이며, f_ck는 22MPa이다. 산정된 콘크리트의 탄성계수는 24,580 MPa이며, 옹벽 벽체와 뒤채움 토사의 접촉면에서의 마찰계수(coefficient of interface friciton)는 0.5를 적용하였다. 옹벽 뒤채움 토사는 점착력이 없는 사질토로 구성하였는데, 점착력을 무시함으로써 중력식 옹벽 상부에서 발생할 수 있는 (-)토압을 억제시켰다.

Table 2. Properties of materials used in the modeling

Table 3. Properties of pavement used in the modeling

옹벽 상부에 포장층을 적용하는 것은 실제 설계조건과 부합하며, 수치해석상 차륜하중에 의해 발생할 수 있는 지반의 국부파괴로 의한 해석 오류를 방지하는 효과를 얻을 수 있었다. 여기서, 지하수위는 존재하지 않는 것으로 가정하였다.

3.4 수치해석단계

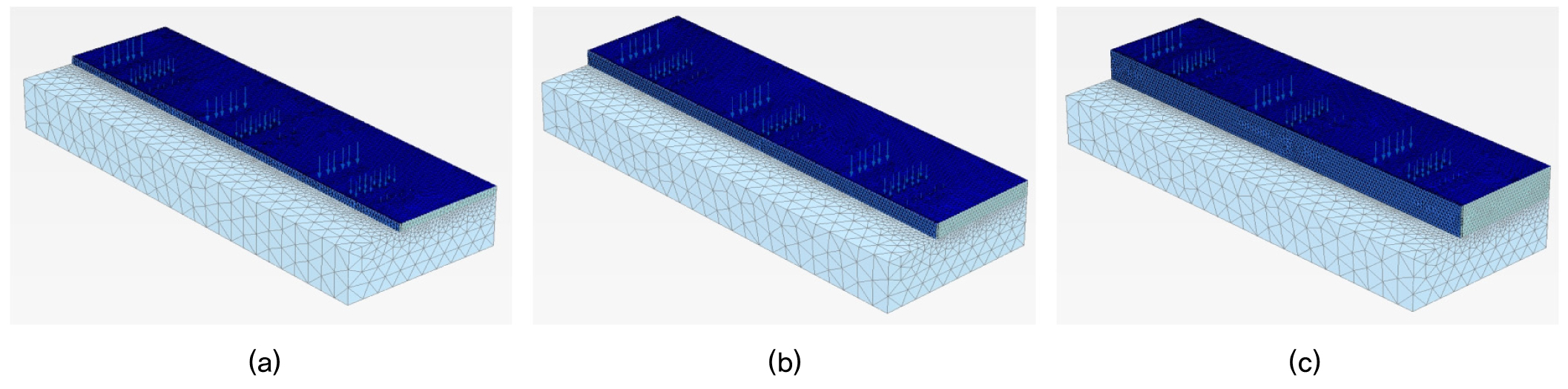
본 해석에 이용된 해석단계는 Case 1, Case 2, Case 3에 관계없이 일정하며, 옹벽배면하중조건(축하중100%, 축하중75%+차선하중4.233kN/m²)과 옹벽의 변위형태(활동변위, 전도변위)에 따라 달라진다. 이때 활동변위 및 전도변위는 변위에 의해 지반파괴가 발생하거나 변위에 의한 h_eq가 일정하게 나타날 때까지 수치해석을 수행하였다. 옹벽배면의 하중조건에 따른 전도변위 및 활동변위에 따른 등가상재하중 높이(h_eq)를 산정하기 위한 수치해석단계는 Table 4와 같다. Fig. 10 및 Fig. 11은 옹벽에 활동변위 및 전도변위가 활성화된 유한요소망을 보여주고 있다.

Table 4. Numerical Analysis calculation stage

Fig. 10.

Activate displacement of wall under point load (100%)

Fig. 11.

Activate displacement of wall under wheel load (75%) + lane load (4.233kN/m²)

4. 수평변위에 따른 등가상재하중높이(H_eq) 산정

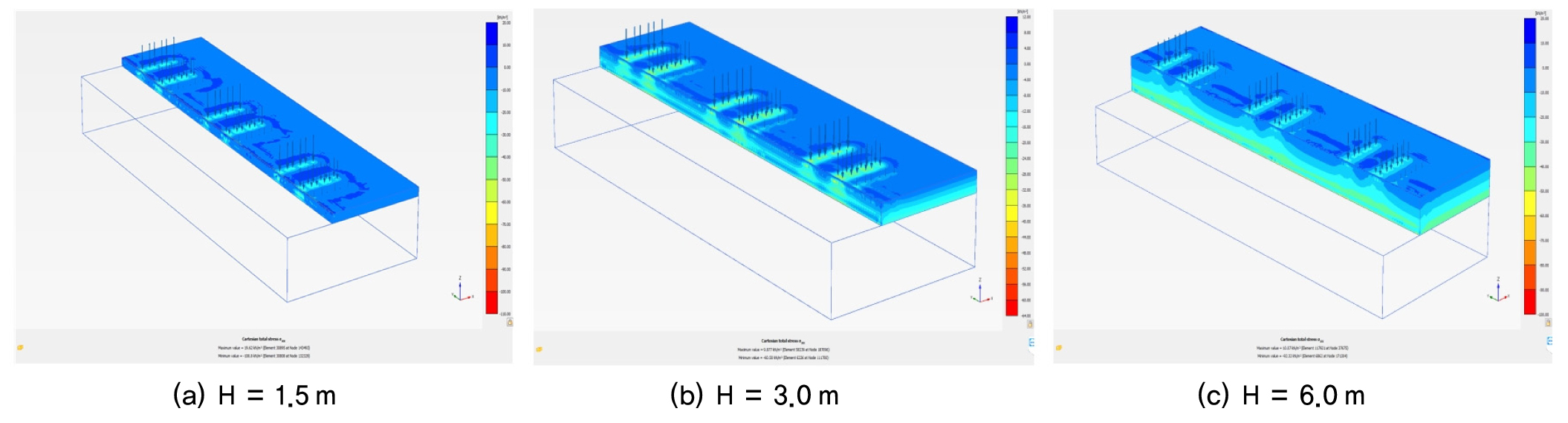
Fig. 12∼14는 국내 표준트럭 하중에 의해 옹벽 및 배면지반에 작용하는 수평토압 등고선을 옹벽 높이에 따라 나타낸 것이다. Case 1 및 Case 2의 경우 축하중이 큰 지점에서 수평토압이 크게 작용하고 있는 것을 확인할 수 있으며, 가장 크게 작용하는 지점은 트럭의 중앙부분 즉, 두 개의 축하중(135kN+135kN)이 집중되는 지점이다. 따라서 안전측으로 설계하는 경우 Case 1과 2에서는 하중이 가장 크게 작용하는 지점에서 수평토압을 산정하여 등가상재하중 높이로 나타내는 것이 타당할 것이다. Case 3의 경우는 옹벽에 작용하는 토압이 균일하게 작용하고 있는 것을 알 수 있다.

Fig. 12.

Lateral pressure contour of retaining wall height in Case 1

Fig. 13.

Lateral pressure contour of retaining wall height in Case 2

Fig. 14.

Lateral pressure contour of retaining wall in Case 3

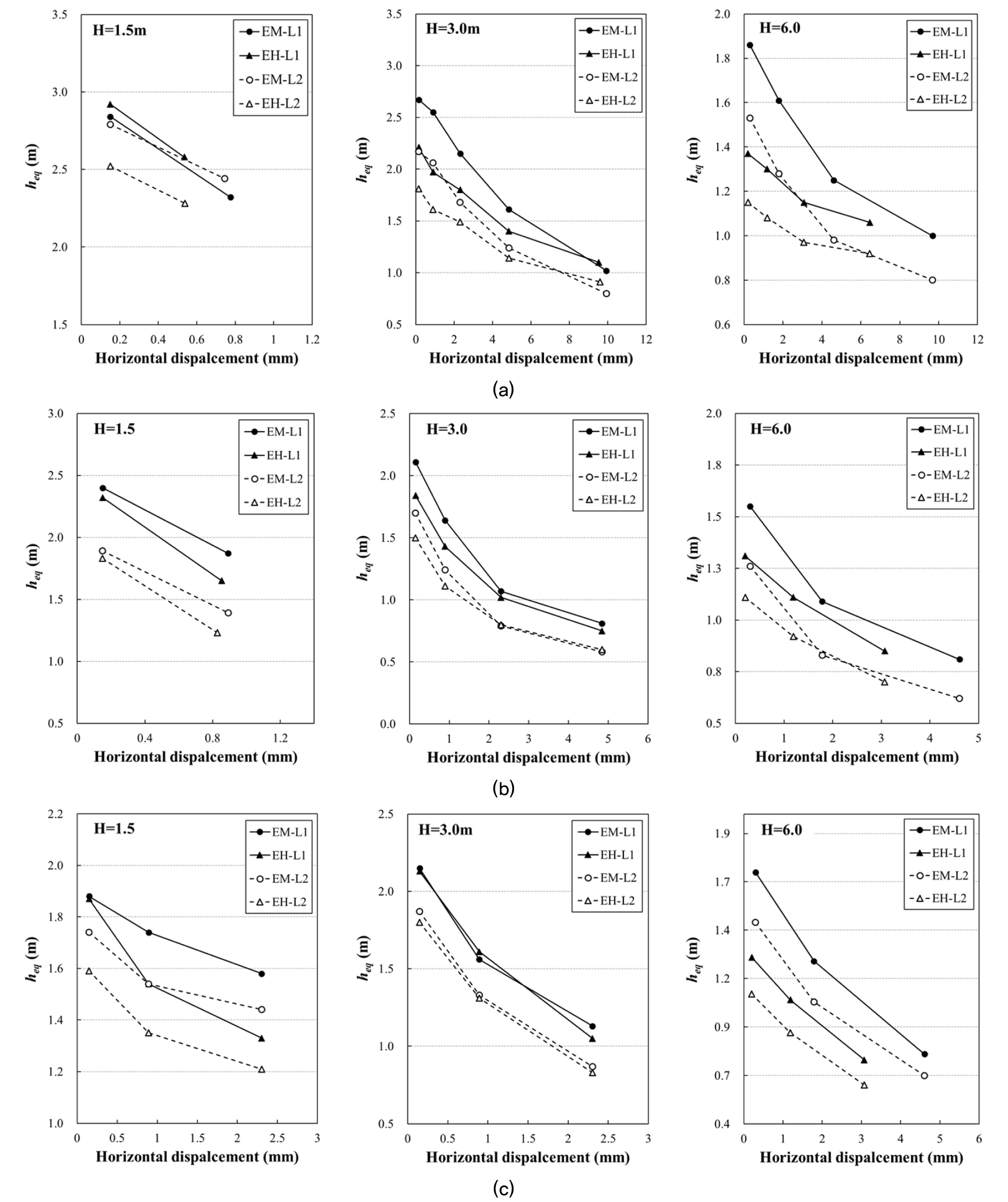
Fig. 15는 상재하중배치(Case 1, Case 2, Case 3), 옹벽높이(H=1.5m, 3.0m, 6.0m), 옹벽배면하중(축하중100%, 축하중75%+차선하중(4.233kN/m²), 옹벽변위(전도변위, 활동변위)조건에 대하여 옹벽의 수평변위에 따른 등가상재하중높이(h_eq)를 나타낸다. 모든 Case에서 옹벽 높이와 관계없이 상재하중을 표준트럭의 축하중 100%로 고려하는 경우 h_eq가 크게 나타났다. Case 1과 2의 결과에 따라 옹벽과 차량의 이격거리가 작은 경우 옹벽에 미치는 영향이 커지는 것을 볼 수 있다. 옹벽의 수평변위가 증가할수록 h_eq는 감소한다. 수평변위 증가로 인해 옹벽배면의 토사가 파괴 될 때 h_eq를 산정하여 Table 5에 제시하였다. 제안된 등가상재하중높이는 AASHTO의 등가상재하중높이 보다 다소 큰 값을 보이고 있으며, 옹벽높이가 낮을수록 등가상재하중 높이는 크게 평가되었다. 옹벽높이가 낮을수록 트럭하중 대부분이 수평토압으로 작용하기 때문으로 판단된다.

본 논문에서는 수치해석을 통한 결과를 근거로 하여 2가지 방법(등가수평력 기준, 등가모멘트 기준)으로 산정된 값보다 상향시킨 등가상재하중높이를 Table 5(*Proposed)와 같이 제안하였다. 이는 이론 및 수치해석 상 동반되는 한계와 불확실성을 반영하고, 옹벽구조물의 장기안정성을 확보하기 위함이다.

Fig. 15.

Equivalent Height due to horizontal displacement; (a) Case 1, (b) Case 2, (c) Case 3 (EM : Equivalent Moment, EH : Equivalent Horizontal force, L1 : Wheel loads 100%, L2 : Wheel loads 75% + Lane loads)

Table 5. Equivalent height of soils (h_eq) on retaining walls (unit: meter)

5. 결 론

국내 표준트럭의 축하중 위치 및 크기, 트럭배치를 반영하여 3차원 수치해석방법을 이용하여 등가상재하중높이(h_eq)를 산정하였으며, 그 결과는 아래와 같다.

(1) 옹벽의 주동토압은 옹벽의 수평변위가 점차 증가하여 옹벽배면의 토사가 팽창파괴 될 때의 토압이므로, 옹벽의 등가상재하중높이(h_eq)는 옹벽배면 트럭하중에 의해 옹벽의 수평변위가 점차 증가하여 옹벽배면의 토사가 팽창파괴 될 때의 토압을 분석하여 이를 적분하여 산정하였다.

(2) Case1 및 Case 2의 경우 트럭하중에 의한 토압증가량은 트럭하중 작용위치에서 인접한 옹벽배면에서 수평토압이 크게 발생하고 있음을 알 수 있으며, 옹벽높이가 낮을수록 트럭하중의 영향이 크게 나타났다.

(3) 제안된 등가상재하중높이(h_eq)는 AASHTO의 등가상재하중높이 보다 큰 값을 보이고 있으며, 옹벽높이가 낮을수록 등가상재하중높이가 크게 평가 되는 경향이 나타났다. 이는 옹벽높이가 낮을수록 트럭하중의 대부분이 수평토압으로 작용한 결과로 판단된다.

(4) 등가상재하중높이는 3차원 수치해석결과를 근거로 하여 등가수평력 및 등가모멘트에 의해 평가된 값보다 큰 값을 제안하였으며, 이는 옹벽구조물의 장기안정성을 확보하기 위함이다.