1. 서 론
2. 이론적 배경
2.1 합성형/조합형 Sheet Pile 공법
2.2 탄소성 해석
2.3 유한요소해석
3. 수치해석
3.1 해석 조건
3.2 지반정수
3.3 유한요소해석
3.4 시공 단계별 해석
4. 결과 분석 및 고찰
4.1 합성형/조합형 Sheet Pile 공법에 관한 고찰
4.2 탄소성 해석에서의 거동
4.3 유한요소해석에서의 거동
4.4 해석방법별 결과 비교
5. 결 론
1. 서 론
국내에서 지반굴착시 주로 적용되고 있는 흙막이 공법은 H-Pile+토류판, Sheet Pile, S.C.W, C.I.P 및 지하연속벽 공법 등이 있다. 이 때, 현장의 토질조건, 지하수위 위치, 인접구조물 유무, 굴착규모 및 굴착심도 등에 따라 공법을 선정하고 추가적으로 경제성과 시공성 등을 함께 고려하여 결정한다. 특히, 지하수위의 영향이 있는 경우 H-Pile+토류판에 그라우팅을 실시하거나 Sheet Pile을 이용한 공법을 보편적으로 적용하고 있다. Sheet Pile 공법은 자체로서 벽체를 형성하며, 이를 통해 배면의 토압 및 수압에 동시에 저항할 수 있는 흙막이 구조물이다. 본 공법은 시공이 간편하고 타 공법에 비해 차수성이 양호하기 때문에 하천과 해안에 인접하여 지하수위의 영향을 많이 받는 굴착 공사에 많이 적용되고 있다(Lee, 2018).
특히, 대규모 석유화학 공장 건설에 따른 해안 매립과 대규모 굴착이 증가하면서, H-Pile과 Sheet Pile을 결합하여 차수성과 휨강성이 우수한 합성형(Composite, Built-up) 또는 조합형(Combine, Interlocking, Welding) Sheet Pile 공법의 적용 사례가 증가하고 있다. 또한, 암반지반에 적용될 수 없는 Sheet pile공법의 한계를 보완하고 장점은 발전시키는 방향으로 개선시킨 H-Pile로 보강된 Sheet Pile 공법 역시 합성형 Sheet Pile 공법의 한 종류로 적용 사례가 증가하고 있다(Park, 2014).
이와 같은 합성형 Sheet Pile은 순차 시공 또는 비 용접을 통해 형성되고, 조합형 Sheet Pile은 용접이나 조합(Interlocking)으로 형성되고 있다. 그러나, 합성형 또는 조합형 Sheet Pile 공법은 국내외 공법 개발사나 제품 제조사에서 제공하는 설계 방법 등을 우선으로 적용하고 있어 체계적인 비교 연구가 미흡한 실정이다. 따라서 다양한 해석 방법 즉, 탄소성 해석과 유한요소해석 등을 통한 관련 해석법의 연구가 요구된다. 이에 본 연구에서는 다양한 합성형 및 조합형 Sheet Pile 공법을 조사하고 각 공법에서 주로 사용하고 있는 흙막이벽(측면말뚝)의 단면 특성과 해석법 등을 비교 분석하였다.
또한, 실제 설계 적용 사례를 조사하여 본 연구에서는 편재하측 반단면 탄소성해석(MIDAS Geo-X)과 단기/장기/압밀 특성과 시공 조건을 고려한 전단면 유한요소해석(Plaxis)을 수행하여 사질토와 점성토가 혼재하는 해안 매립지반에서 조합형 Sheet Pile의 거동을 평가하고자 하였다.
2. 이론적 배경
본 연구에서 고려한 흙막이벽은 조합형 Sheet Pile로 국내외에서 다양한 형태로 적용되고 있다. 일반적으로 적용되는 조합형 Sheet Pile 공법의 단면은 비대칭 조건으로 편토압이 작용하는데, 이와 같이 편토압이 작용하는 측면말뚝은 굴착에 따라서 벽체의 변위 방향이 크게 변화할 수 있으며, 그에 따른 토압도 크게 변화한다. 편토압이 작용하게 되면 큰 변형이나 흙막이벽의 붕괴를 유발할 수 있으므로 편토압을 고려한 해석이 요구된다. 이하에서는 합성형 및 조합형 Sheet Pile 공법과 본 공법의 해석 방법을 제시하였다.
2.1 합성형/조합형 Sheet Pile 공법
합성형 및 조합형 Sheet Pile 공법은 H-Pile과 Sheet Pile을 합성 또는 조합해서 흙막이 벽체를 형성하는 공법으로 Sheet Pile과 H-Pile이 합성됨으로 인해 각각의 부재들이 받는 외력이 분산되어 각 부재가 부담하는 부재력이 감소되고, Sheet Pile과 H-Pile이 완전한 접합이 아닌 부분적으로 접합되어도 단일벽체에 비하여 벽체 강성에 유리하게 영향을 미칠 수 있는 것으로 알려져 있다.
Park(2014)에 따르면 동일한 조건에서 H-Pile만 있는 경우, Sheet Pile만 있는 경우, 합성벽체인 경우에 대한 수치해석 결과, 지주파일인 H-Pile의 경우 단일벽체에 비해 합성벽체인 경우 전단력은 13%, 휨모멘트는 30% 가량 작게 나타났고, 변위는 90%정도 작게 예측되었음을 제시하였다. 또한, Sheet Pile의 경우도 단일벽체인 경우보다 합성벽체인 경우 부재력과 변위가 작게 나타나고 있는데 단일벽체에 비하여 합성벽체의 Sheet Pile 부재력값은 전단력의 경우 21%, 휨모멘트 18%, 변위 4%정도 작게 평가됨을 제시하였다.
Cho(2014)는 3차원 수치해석을 통해 Sheet Pile과 H-Pile 연결부재에 작용하는 평균 응력분담비를 평가하였고, 2.4∼ 5.0으로 H-Pile이 더 큰 응력을 분담하였으며, Sheet Pile의 두께가 증가할수록 평균 응력분담비가 작아져 Sheet Pile의 응력분담이 증가하는 경향을 나타낸다고 제시하였다.
Lee(2018)는 Steel H-Pile과 Plastic Sheet Pile이 결합된 복합구조의 토류벽체 거동을 파악하기 위하여 3차원 수치해석을 실시하여 Arching 현상과 Plastic Sheet Pile의 인장력으로 인해 Plastic Sheet Pile에 작용하는 토압의 상당부분이 H-Pile로 전이되어 H-Pile에 대한 Plastic Sheet Pile의 부재 할당 모멘트 비율이 매우 작게 나타남을 제시하였다.
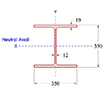
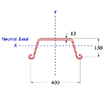
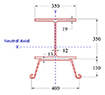
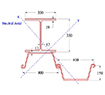
합성형 또는 조합형 Sheet Pile 공법은 Table 1과 같이 다양한 형태로 활용되고 있다. 일반적으로 Type 01과 Type 02의 경우 조합형으로 적용되고 있고, Type 03와 Type 04는 합성형으로 적용되고 있다. 특히, Type 02의 경우 I형강을 합성한 대단면으로 이용되고 있고, Type 03과 같은 경우는 암반 등 천공 굴착을 통해 흙막이벽을 설치해야 하는 경우 이용하고 있다. 일반적으로 강재는 인장강도가 크기 때문에 배면에 H-Pile을 설치하여 중립축을 외부로 이동시키는 경우가 유리할 것으로 판단되고, 내측에 설치하면 외곽부로 Sheet Pile이 돌출되어야 하고 이로 인해 부지 사용량이 증가하는 특징을 가지고 있다. 국내의 경우 위의 4가지 조건에 대한 공법이 모두 적용되고 있다.
Table 1.
Application Type of Composite and Combine Sheet Pile
| Type | Type 01 | Type 02 | Type 03 | Type 04 | Photograph |
|
Weld- ing | 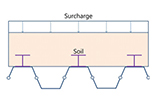 | 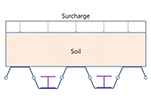 | 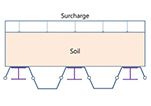 | 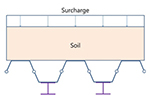 |  |
|
Inter- locking | 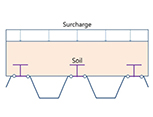 | 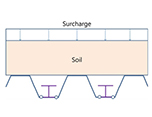 | 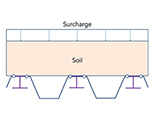 | 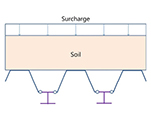 |  |
조합형 Sheet Pile 벽체의 해석법은 일반적인 Sheet Pile 설계법(연속벽)이나 엄지말뚝 설계법을 적용하고 있고, 내적 안정성 검토 방법으로는 최소 강도법(M.O.F., 2016)과 모멘트 분배법(ArcelorMittal, 2020)을 이용하고 있다. 모멘트 분배법의 경우 국내에서는 응력분담비법으로 알려져 있고(Cho, 2014), H-Pile과 Sheet Pile의 휨강성 비율대로 발생 모멘트를 분배하여 적용한다.
2.2 탄소성 해석
탄소성 해석은 흙-구조물 상호작용을 고려하는 해석법으로 흙막이벽은 탄성보, 버팀보는 탄성 스프링, 지반은 탄소성 스프링으로 모델링하여 초기 토압을 가한 후 발생하는 변위를 계산한다. 이 후 발생 변위에 상응하는 지반의 탄소성 상태를 판단하고 토압을 보정하여 다시 변위를 계산하는 반복과정을 통하여, 흙막이벽의 변위, 응력 및 버팀보의 반력을 계산하는 해석법이다.
본 연구에서의 탄소성 해석은 MIDAS Geo-X(Ver. 4.6) 프로그램을 이용하였고, 반단면 해석으로 편하중이 재하되는 벽을 단독으로 계산하였다. 본 해석 방법의 경우 하중이 대칭인 조건으로 계산하기 때문에 마주보는 벽의 영향을 고려할 수 없지만 합성형, 조합형 Sheet Pile의 다양한 형태와 해석 방법을 쉽게 적용할 수 있고 현재까지 흙막이 가시설 설계에서 꾸준히 적용되어 검증된 방법이다.
2.3 유한요소해석
유한요소해석(FEM)은 Plaxis(Ver. 8.6)를 이용하였다. 본 프로그램은 복잡한 지반조건 및 시공조건 등을 고려할 수 있고 전단면 해석으로 양벽 모두 해석이 가능하다.
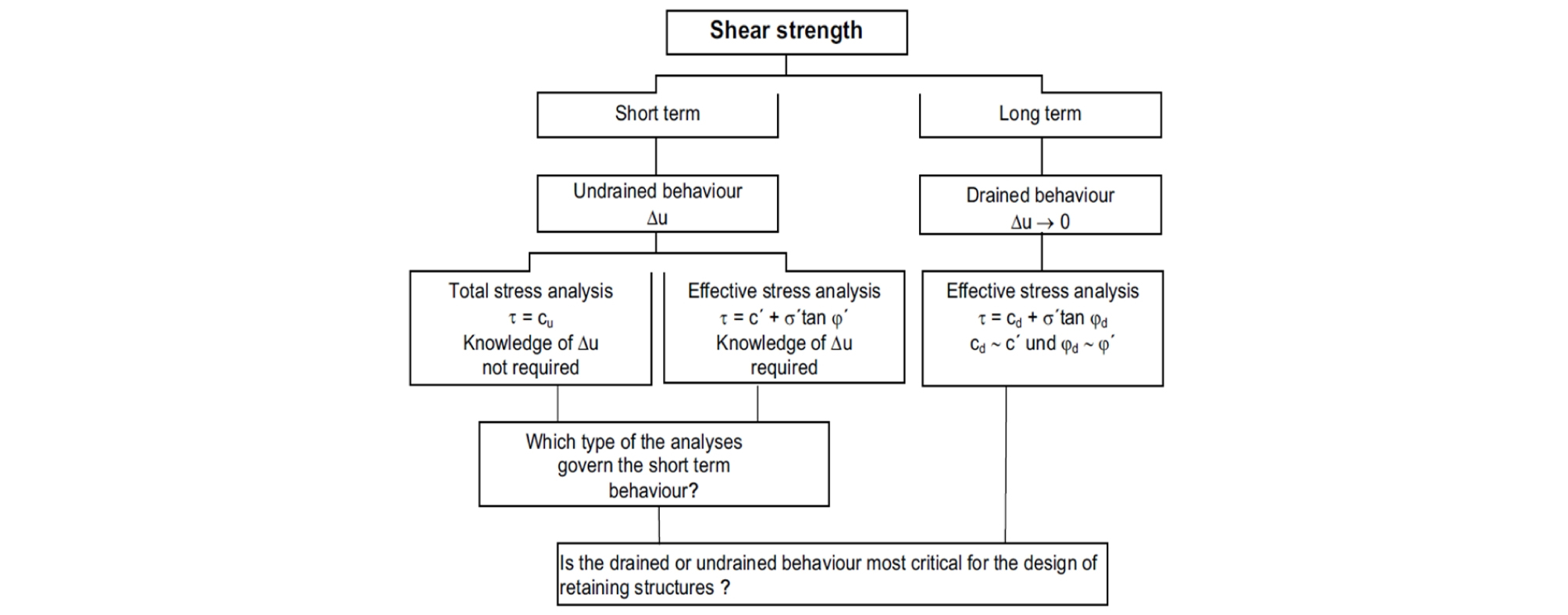
일반적인 흙막이 가시설의 경우 활동력인 주동토압이 단기가 장기보다 크고, 저항력인 수동토압이 장기가 단기보다 크므로 단기가 더 위험측인 것으로 알려져 있으나, 독일 굴착위원회(EAB, 2006), Kempfert and Gebreselassie (2006)은 점토의 경우 과잉간극수압이 발생되므로 단기 안정성과 장기 안정성 모두 확인할 필요가 있다고 제시하였다(Fig. 1). 점성토의 단기와 장기 안정성은 전단 파라미터와 해석 방법에 따라 평가할 수 있다(Kim et al., 2018). 본 연구에서 단기 안정성(비배수 거동)중 전응력 해석은 UU 파라미터, 유효응력 해석은 파라미터, 장기의 안정성(배수 거동)은 CD, 파라미터를 적용하였다.
3. 수치해석
3.1 해석 조건
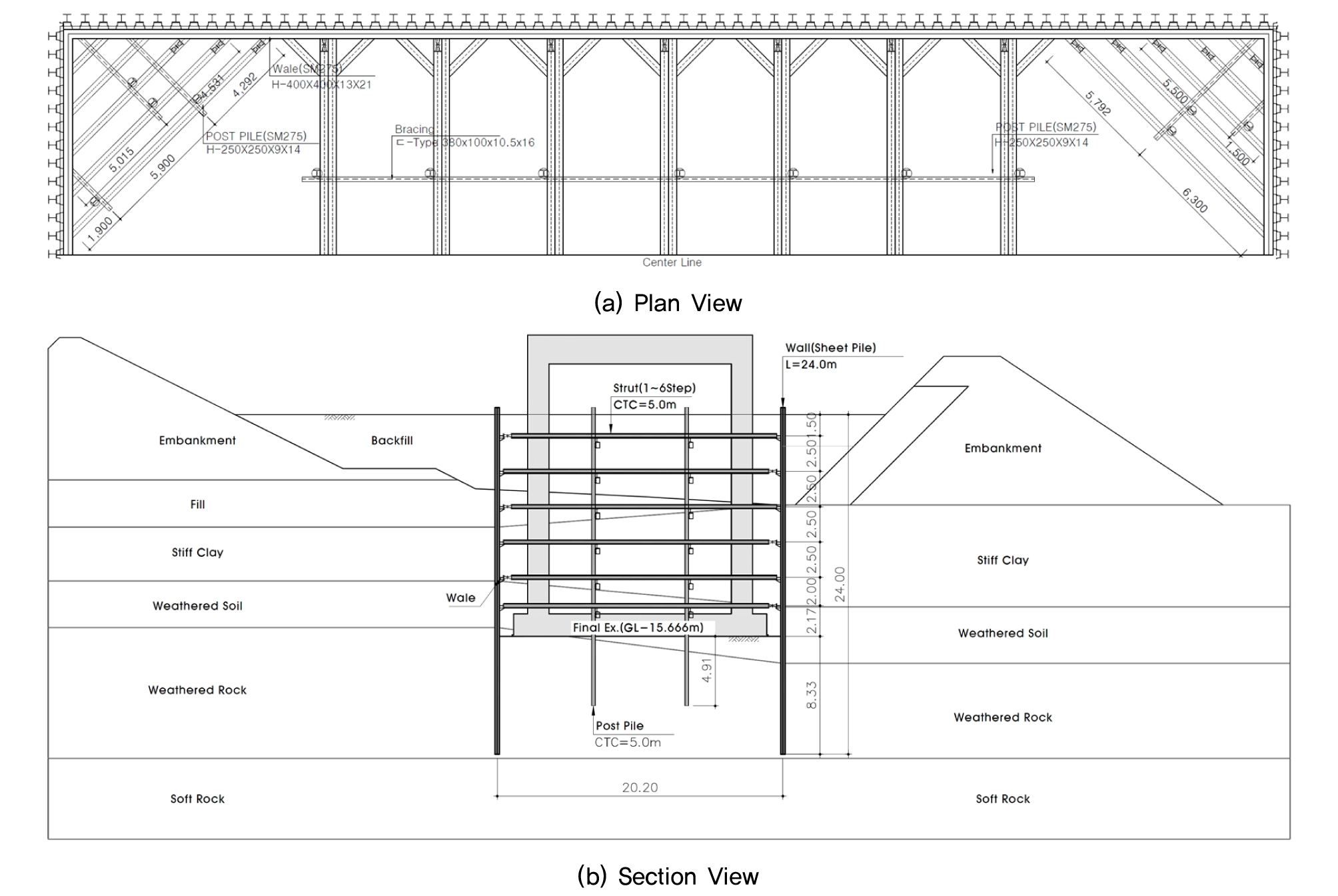
본 연구에서의 조합형 Sheet Pile 공법을 적용한 흙막이 가시설의 평면과 단면은 Fig. 2와 같다. 견고한 점성토 상부에 준설 매립된 모래층이 존재하고, 그 상부에 측면말뚝(조합형 Sheet Pile) 시공 등을 위해 추가 매립된 모래층이 존재한다. 또한, 본 사례에서는 좌/우측에 경사식 호안이 축조되어 해수의 유입을 방지하고자 하였다. 최종 15.7m를 굴착함에 있어 수평 7단, 연직 6단의 2열 버팀보를 설치하였고, 중간말뚝 등을 설치하여 좌굴, 처짐 등 부재력을 감소시키고자 하였다. Table 2에는 본 해석에서 적용한 주요 부재에 대한 제원을 제시하였다.
Table 2.
Members used in Numerical Analysis
| Members | Member Type and Properties |
| Wall |
H-Pile + U Sheet-Pile : H-350×350×12/19[SM355], SP-400×150×13(SY400), L=24.00 m |
| Strut | Strut 1~6 Step : 2H-350×350×12/19[SM275], CTC=5.00 m |
3.2 지반정수
수치해석은 계산조건 및 지반정수 등에 따라 결과의 편차가 매우 크므로, 신뢰성 높은 지반의 거동을 예측하기 위해서는 적합한 구성모델과 지반 및 구조물의 특성치를 적용해야 한다. Kim et al.(2013)에 따르면 탄소성 해석법에 적용되는 주요 매개변수 중 점착력이 재료의 거동에 큰 영향을 주는 것으로 제시되었고, 현장의 지반조사 결과가 설계시 조사결과와 다를 수 있으므로 주의가 요구됨을 제시하였다. 이에 탄소성 해석을 위한 설계 지반정수는 지반조사와 문헌을 참조하여 신중하게 결정하였고, 그 결과는 Table 3과 같다(H.O.B, 2013). 또한, 유한요소해석을 위한 부재의 설계정수는 Table 4와 같다.
Table 3.
Soil Properties
Table 4.
Structure Member Properties
| Members |
Area (m2) |
Moment of Inertia (m4) |
Elastic Modulus (MPa) |
Poisson's Ratio (-) |
| Wall(/m) | 4.07E-02 | 1.77E-03 | 200,000 | 0.30 |
| Strut(/EA) | 1.74E-02 | 4.03E-03 | 200,000 | - |
유한요소해석을 위한 설계 지반정수는 탄소성 해석과 동일하고, 견고한 점토만이 추가 파라미터가 요구되어 다음과 같이 결정하였다.
비배수 파라미터 중 마찰각은 “0”(=0), 비배수 전단강도는 견고한 점토에 대한 실험값인 60kPa을 적용하였고, 비배수 파라미터 중 변형계수는 2가지 방법 중 탄소성해석과 동일한 값의 방법 2를 고려하여 적용하였다(Table 5 참조).
Table 5.
Elastic Modulus of Stiff Clay
| Method | Method 1 | Method 2 | |
|
Strength Method (Undrained) | Design Parameter | ||
| E' (Drained) | Eu (Undrained) | ||
| Formula | Design Parameter | ||
| Elastic Modulus (kPa) | 12,000~49,200 | 5,833 | 7,000 |
| Application (kPa) | 7,000 | ||
유효 파라미터는 삼축압축 실험결과(H.O.B., 2013)와 기존 문헌을 참조하여 본 연구에서 Table 6과 같이 결정하였고, 배수 탄성계수는 비배수 탄성계수 산정시 기 산정된 값(E'=5,833kPa)을 적용하였다.
Table 6.
Effective Parameters of Stiff Clay
| References | Data | Cohesion (kN/m2) | Friction Angle (°) | Remarks |
| H.O.B (2013) | Sample-01 | 18.5 | 16.3 | CL |
| Sample-02 | 16.6 | 14.0 | CL | |
| Sample-03 | 9.8 | 16.6 | CL | |
| Kim et al. (2018) | 25 Data | 7.8 | 16.4 | Korea |
| Bouduin et al. (2000) | 8Data | 9.0 | 21.0 | Back Analysis |
| AS 4678 (2002) | - | Under 10.0 | 17.0~32.0 | 2002 |
| Application | 36 Data | 10.0 | 17.0 | Average |
배수 파라미터는 삼축압축 실험결과와 기존 문헌을 참조하여 결정하였고(Table 7), 배수 탄성계수는 비배수 탄성계수 산정시 기 산정된 값(E'=5,833kPa)을 적용하였다.
Table 7.
Drained Parameters of Stiff Clay
| References | Data | Cohesion (kN/m2) | Friction Angle (°) | Remarks |
| H.O.B (2013) | Sample-01 | 12.0 | 28.0 | CL |
| Sample-02 | 6.1 | 26.9 | CL | |
| Sample-03 | 7.6 | 26.5 | CL | |
| Kim et al. (2018) | 25 Data | 5.3 | 25.2 | Korea |
| Bouduin et al. (2000) | 8 Data | 10.0 | 24.0 | Back Analysis |
|
Road Design Technique (2009) | - | Under 50 | 25.0 | Stiff Clay |
| AS 4678 | - | Under 10.0 | 17.0~32.0 | 2002 |
| Application | 38 Data | 7.0 | 26.0 | Average |
3.3 유한요소해석
사질토와 점성토가 혼재하는 지반에서의 굴착시 발생 및 소산되는 과잉간극수압의 크기에 따라 흙막이 벽체의 단기 안정성과 장기 안정성이 영향을 받는다. 따라서, 단기 안정성과 장기 안정성을 확인하고자 유한요소해석을 실시하였으며, 해석 조건은 독일 굴착위원회의 권장사항 등을 참조하여 아래와 같이 Case 1∼Case 3을 적용하였다. Table 8의 최하단을 참고하면 유효응력해석의 장기 조건은 단기 유효응력 및 전응력 해석보다 항상 작은 토압이 발생하므로 해석조건에서 생략하였고, 압밀해석은 공사 기간과 투수계수에 따라 단기 또는 장기 해석이 되므로 구별하지 않았다.
Table 8.
The Type of Numerical Analysis
3.4 시공 단계별 해석
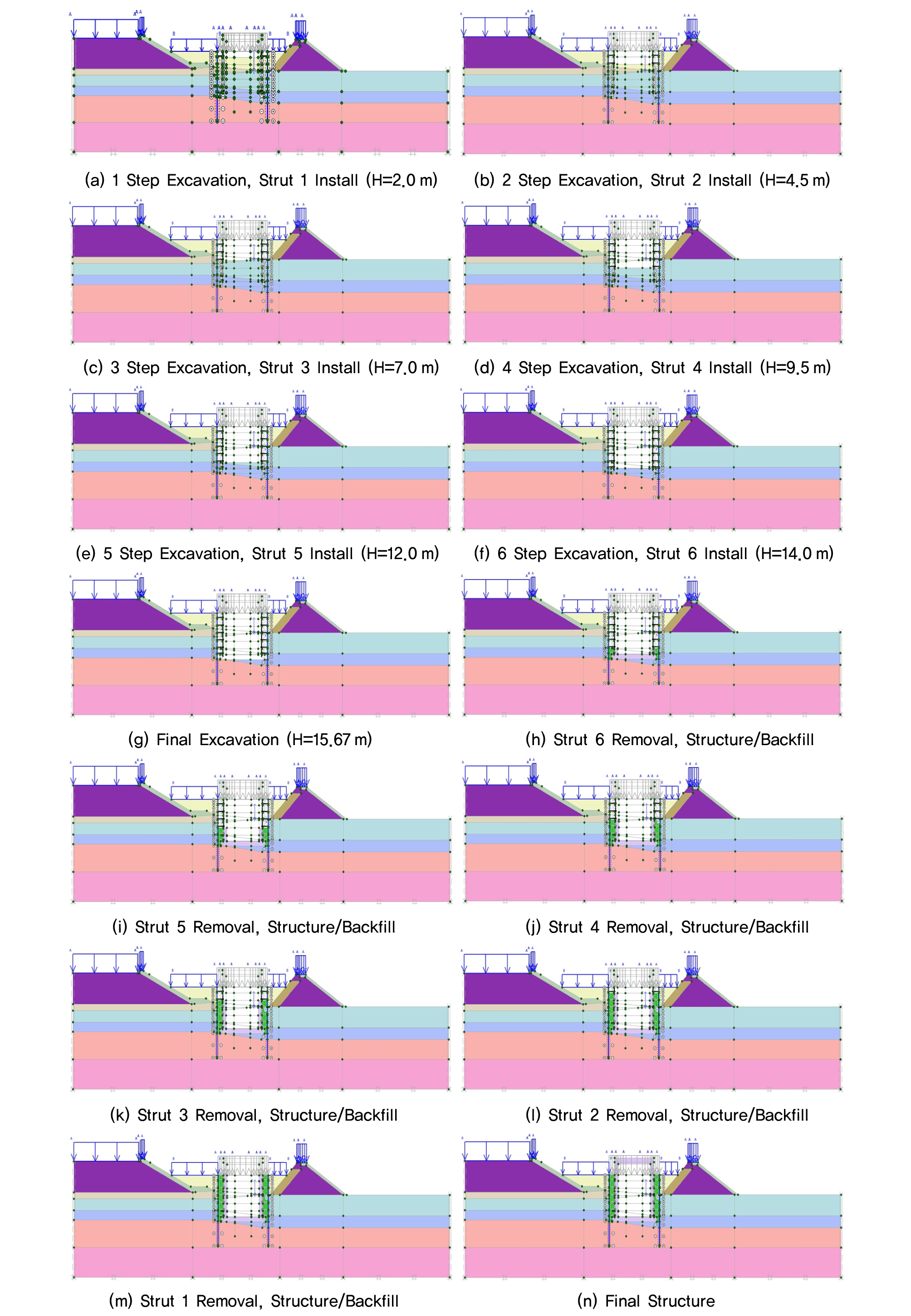
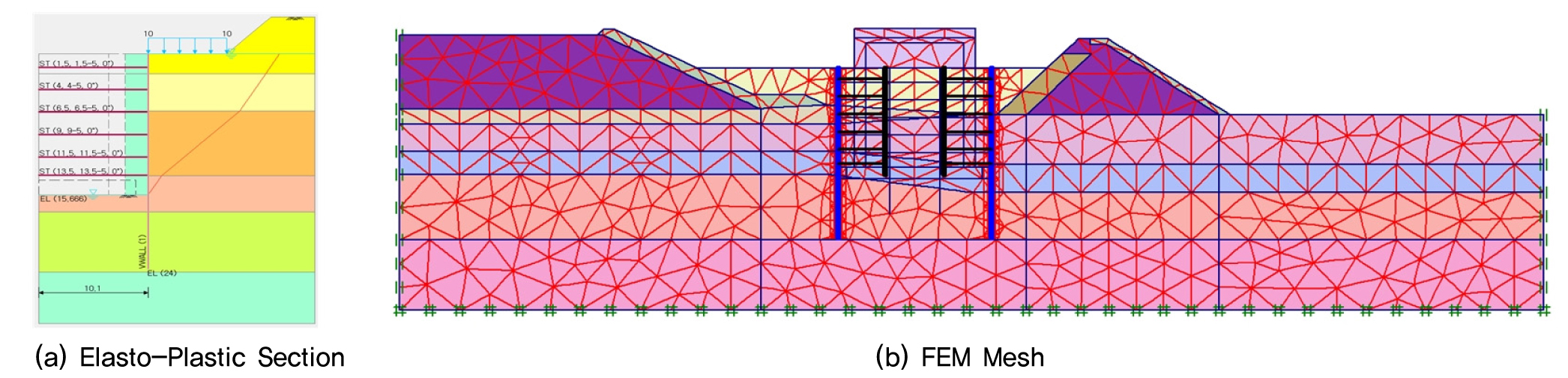
시공 단계를 고려한 해석 단계는 Fig. 3과 같이 적용하였으며, 탄소성 해석과 유한요소해석 모두 동일하게 적용하였다. 다만, 탄소성 해석의 경우 구조물 및 되메우기 높이를 측면말뚝 높이보다 높게 지정할 수 없어 지표면까지 구조물 시공 및 되메우기 하는 것으로 고려하였다(Fig. 4 참조).
4. 결과 분석 및 고찰
4.1 합성형/조합형 Sheet Pile 공법에 관한 고찰
본 연구에서는 국내외에서 일반적으로 적용되는 합성형과 조합형의 대표 단면에 대한 단면 특성을 평가하였고, 그 결과는 아래의 Table 9와 같다. H-Pile 또는 Sheet Pile 단독 또는 단순 총합의 단면성능보다 두 부재를 조합하는 것이 단면성능 개선에 크게 도움되는 것을 확인하였다. Table 9에 제시된 등가 무게(Eq. W)는 H-Pile과 동일한 단면 2차모멘트를 갖기 위해 필요한 강재의 단위중량을 계산한 것으로, 수치가 작을수록 단위무게당 단면성능이 우수하므로 경제성도 증가하는 것을 의미한다(Nippon Steel and Sumitomo, 2016). 조합형 Sheet Pile(Application 1∼3)만 비교하는 경우 H-Pile과 Z형 Sheet Pile을 조합하는 것(Application 3)이 단면성능 측면에서 우수한 것으로 평가되었다.
Table 9.
Material Properties of Combined Sheet Pile
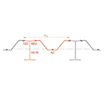
본 연구를 통해 조사한 결과, 조합형 Sheet Pile 벽체의 해석법은 크게 2가지로 적용되고 있음을 확인하였다. 첫째는 일반적인 Sheet Pile 설계법(연속벽)을 적용하되 합성된 부재가 단일 부재라 간주한 단면 특성(단면계수, 단면2차모멘트 등)을 고려하는 방법이다. 둘째는 Eurocode 3 설계법으로 Primary Element와 Secondary Element로 구분하여 Primary Element를 엄지말뚝으로 간주하는 설계법이다(Fig. 5). Type 1의 경우 H-Pile과 Sheet Pile이 Interlocking으로 직접 연결되고 Sheet Pile과 Sheet Pile도 Interlocking으로 연결된다. 이 때, H-Pile이 Primary Element이다. Type 2(Welding Type, High Modulus)는 1개로 용접된 H-Pile과 Sheet Pile이 바로 Interlocking되는 것으로 제시되어 있다. 또한, H-Pile과 용접된 Sheet Pile 전체를 Primary로 간주한다.
흙막이 벽체의 발생 부재력이 결정되면 내적 안정성 검토를 수행하는데, 이 방법도 크게 2가지 방법이 존재한다. 첫째, 최소 강도법으로 용접 부재 중 작은 값을 설계 허용강도로 간주한다. 국내 항만 및 어항설계기준(M.O.F., 2016), 강교 설계 기준(M.L.I.T., 2019)에서 용접시 접합부의 강도는 최소 부재의 값을 적용해야 한다는 기준을 따른 것이다(식 (1) 참조). 둘째, 모멘트 분배법으로 굴착시 발생되는 흙막이벽의 모멘트를 각각의 부재가 각각 분담한다는 개념(ArcelorMittal, 2020)으로, H-Pile과 중간의 Sheet Pile의 모멘트 분배 또는 결합된 파일의 H-Pile과 Sheet Pile에 모두 적용 가능하다(식 (2) 참조). ArcelorMittal(2020)의 경우 Interlocking으로 연결된 부재의 모멘트 비율 산정시 총 단면2차모멘트(벽체)(Iwall=IH-Pile+ISheet Pile)와 각 부재의 모멘트를 이용한다. 국내에서는 응력분담비법으로 알려져 있고(Cho, 2014) H-Pile과 Sheet Pile의 휨강성 비율대로 발생 모멘트를 분배한다.
| $$최\mathrm 소\;\mathrm{강도법},\;\sigma_a=Min.\left(\sigma_H,\sigma_{S/P}\right)\geqq\sigma_{calculation}$$ | (1) |
여기서, σcalculation : 합성 단면에 대한 발생응력
σH : H-Pile의 허용응력
σS/P : Sheet Pile의 허용응력
σcalculation i : 모멘트 분배법으로 계산된 각 부재의 발생 응력
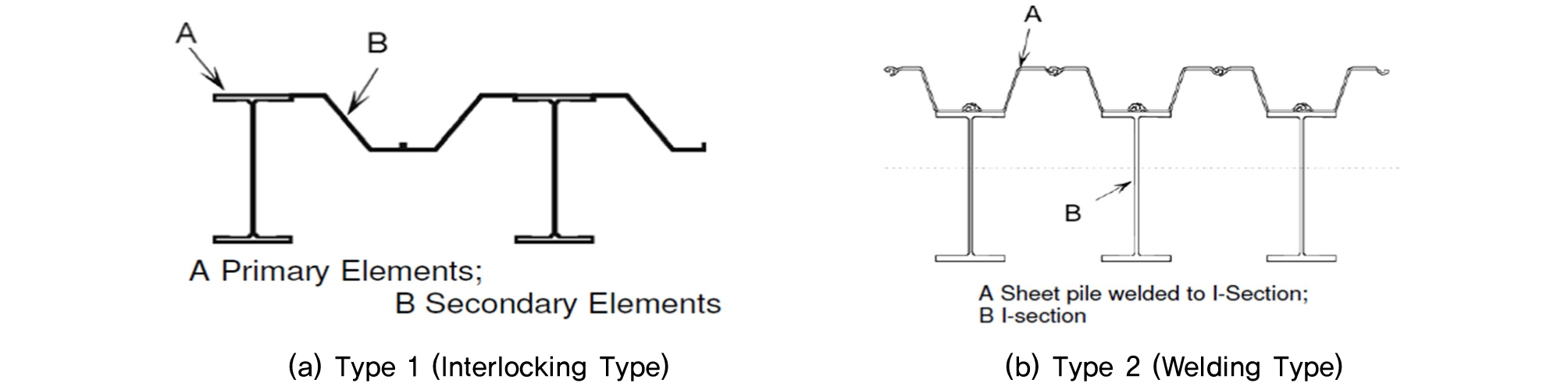
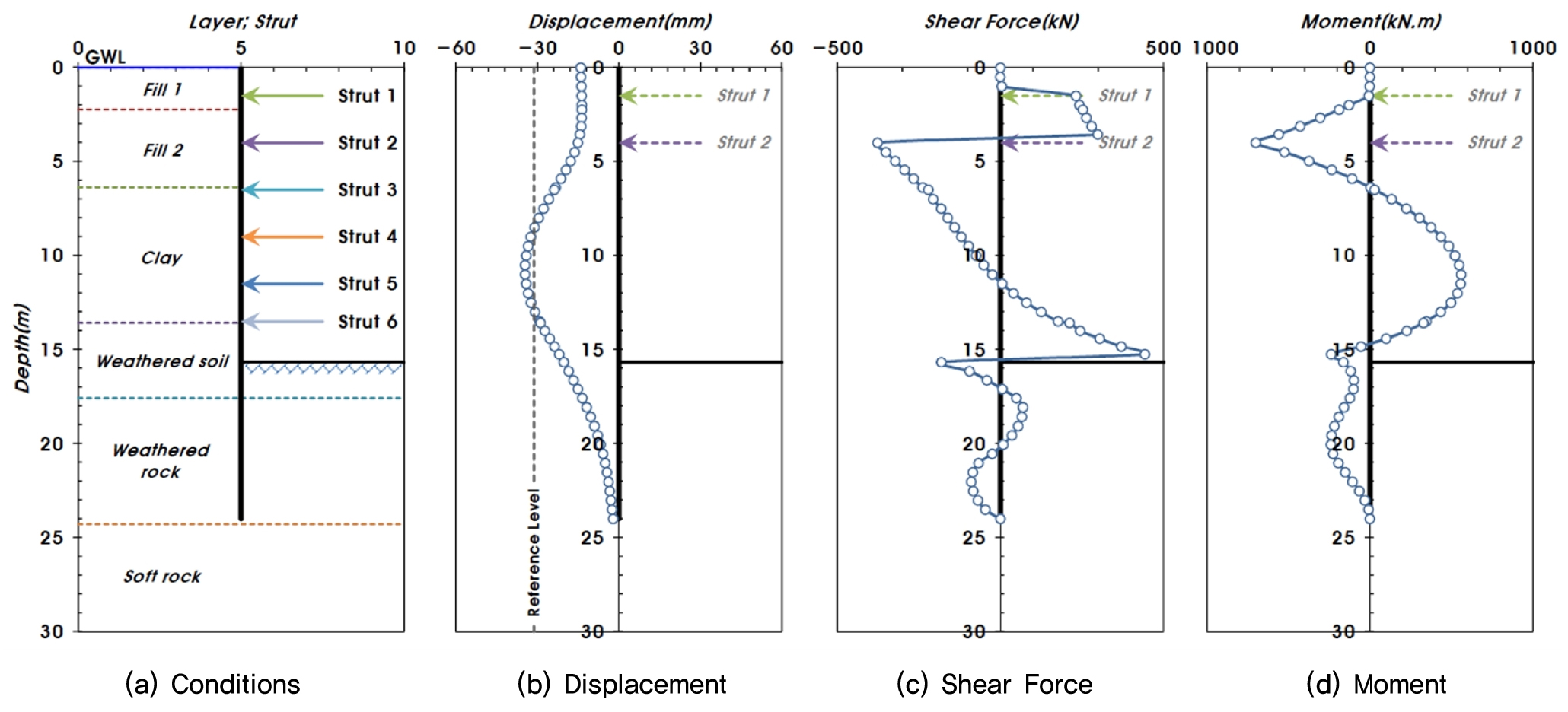
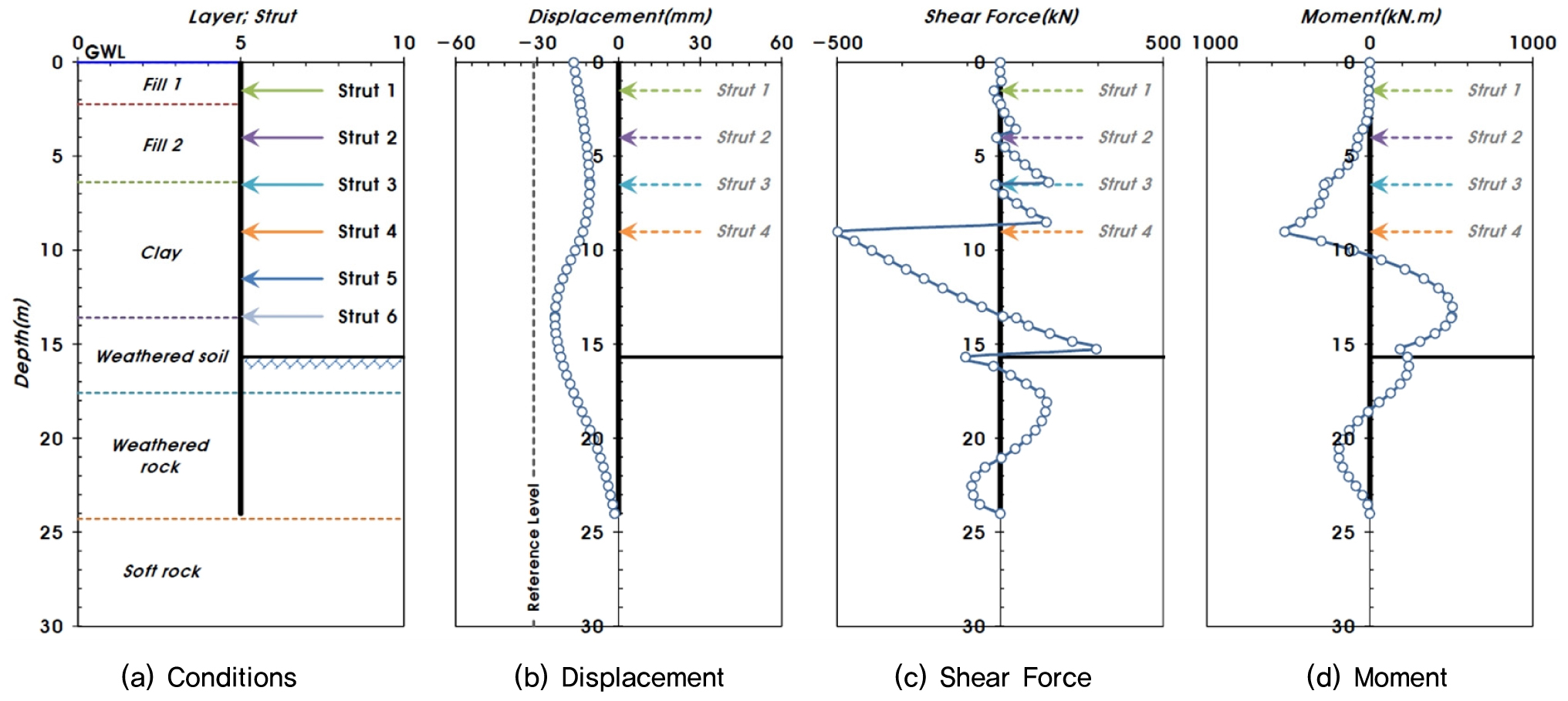
본 연구에서는 위에 제시한 해석법과 대상 단면을 적용하여 탄소성 해석을 수행하였고, Fig. 6에 그 결과를 제시하였다. 해석은 H-Pile만 고려하는 엄지말뚝 해석법(Fig. 5의 Type 1), H-Pile과 용접으로 결합된 Sheet Pile을 하나의 엄지말뚝으로 해석하는 방법(Fig. 5의 Type 2), 전체 단면 특성을 고려한 연속벽체 해석법에 대하여 실시하였다. 해석 결과 연속벽체 해석법에서 변위, 전단력, 모멘트가 엄지말뚝 해석법(Type 1∼2)보다 더 큰 것으로 평가되어 보수적인 결과를 제시하였다.
4.2 탄소성 해석에서의 거동
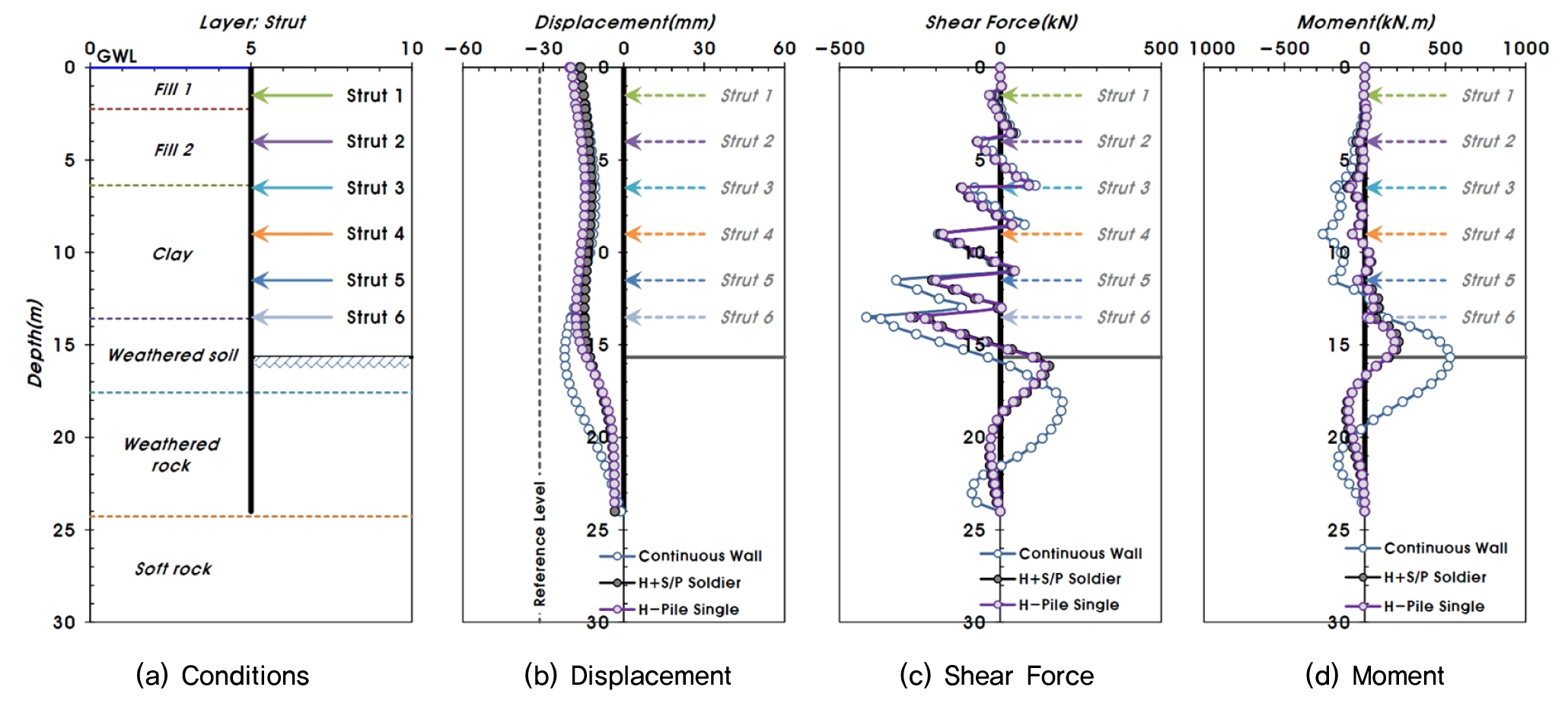
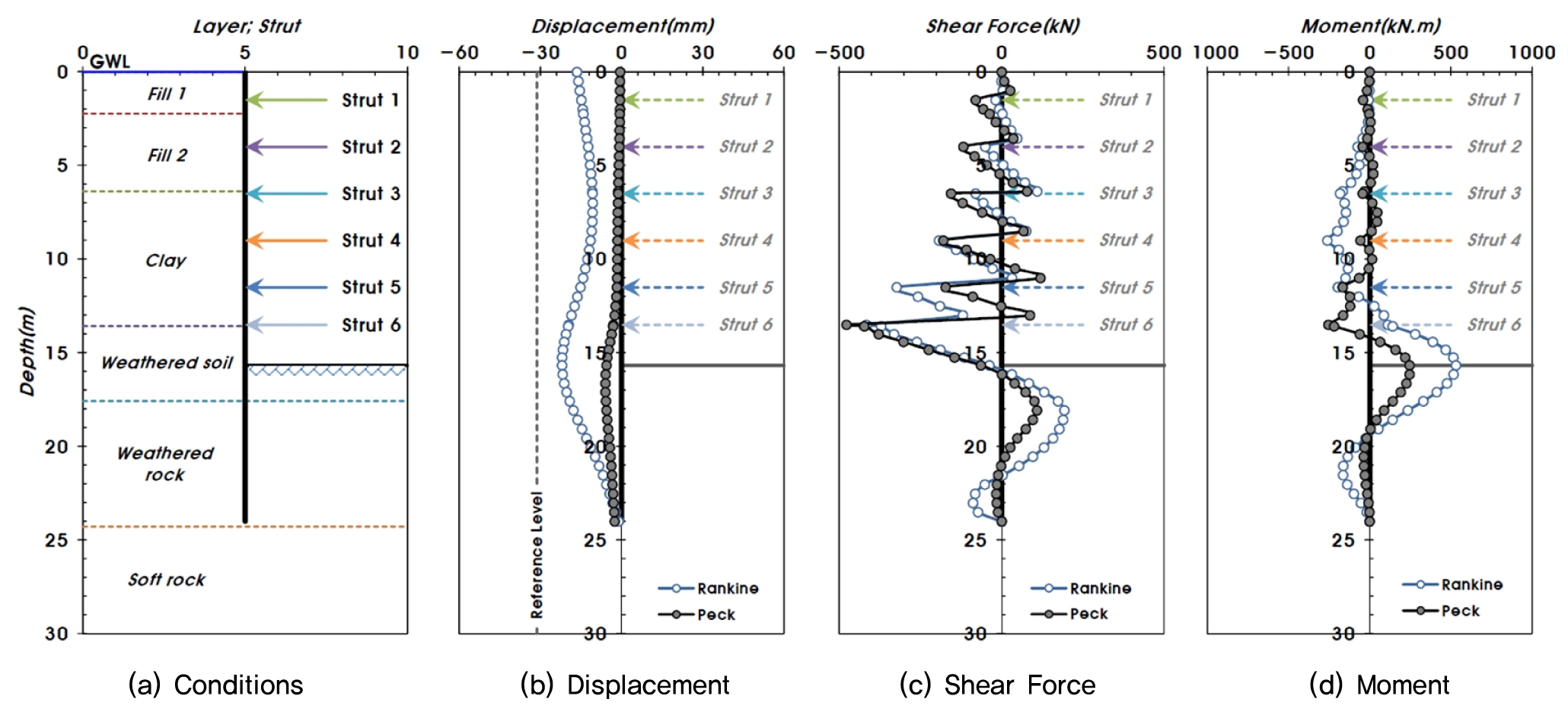
연속벽체 해석법의 결과가 부재력과 변위 측면에서 안전측 설계를 유도하는 바, 본 해석법을 적용한 시공단계별 탄소성 해석결과를 토대로 조합형 Sheet Pile 벽체(측면말뚝), 버팀보의 안정성을 검토하였다. 일반적인 흙막이 거동 해석에서는 최종 굴착 단계에서 이론토압과 경험토압을 비교하여 부재력 등의 안정성을 확인한다. 이에 본 연구에서도 두 토압을 적용하여 안정성을 확인하고자 하였다. Fig. 7에 제시된 바와 같이 최종 굴착단계에서의 변위, 전단력, 모멘트는 Rankine 토압 적용시에 비하여 Peck 토압 적용시 더 작게 나타났고, 각각의 최대값은 최종 굴착면 부근에서 발생하였다.
전체 시공단계를 분석한 결과 휨모멘트는 3단 버팀보 해체 및 구조물/되메우기 단계, 전단력은 5단 버팀보 해체 및 구조물/되메우기 시공단계에서 가장 큰 것으로 나타났으며, 각각의 부재력도는 다음과 같다(Fig. 8∼Fig. 9).
최대 부재력을 토대로 각 부재별 안정성을 검토한 결과, 측면말뚝과 버팀보 모두 안정한 것으로 평가되었다(Table 10). 발생응력과 허용응력의 비로 정의되는 응력비를 분석하면 측면말뚝의 경우 휨, 버팀보의 경우 조합응력에서 최대값을 나타내었다. 따라서, 조합형 Sheet Pile 공법의 경우 휨에 의해 Sheet Pile의 안정성이 지배됨을 알 수 있었고, 버팀보의 경우 조합응력에 의해 지배됨을 알 수 있었다.
측면말뚝 발생변위의 경우 최종 굴착단계부터 버팀보 해체 및 구조물/되메우기 시공이 진행됨에 따라 지속적으로 증가하는 경향을 보였다(Table 11). 특히, 전단력이 최대값인 5단 버팀보 해체와 휨모멘트가 최대였던 3단 버팀보 해체단계에서 급격히 증가하였다.
Table 10.
Analysis Results (Member Force)
Table 11.
Analysis Results (Displacement)
4.3 유한요소해석에서의 거동
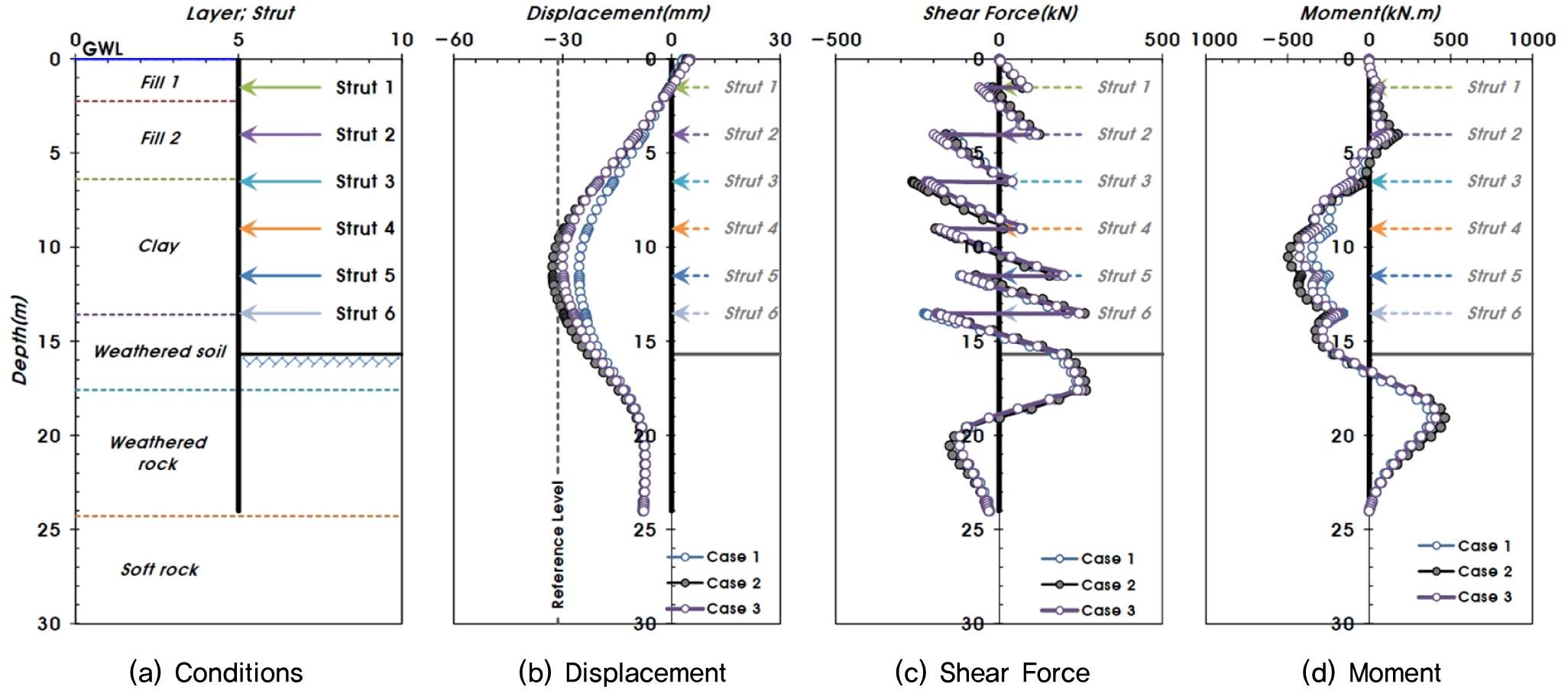
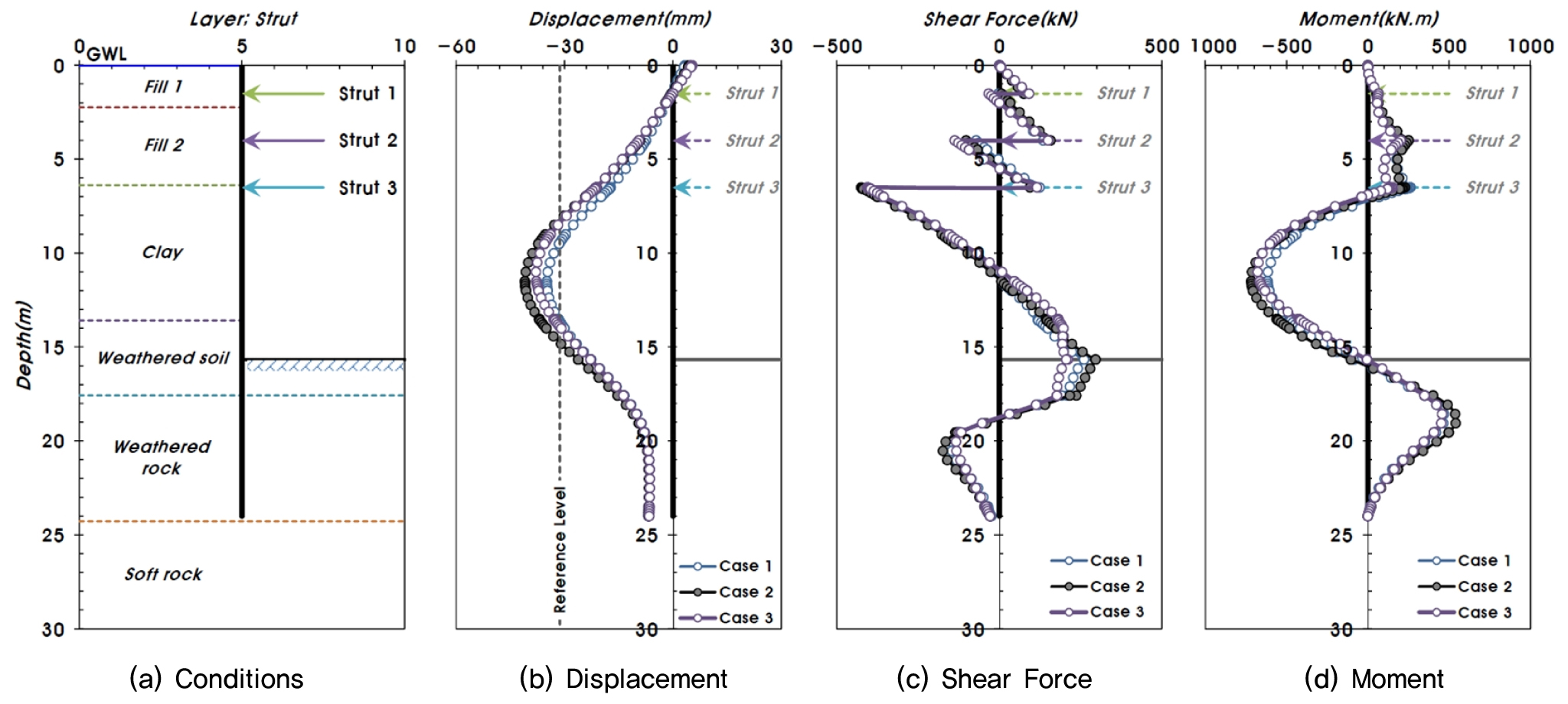
탄소성 해석과 같이 유한요소해석 결과도 최종 굴착단계와 버팀보 해체 및 구조물 시공단계에서의 해석조건별 변위, 전단력, 모멘트를 비교하였다. 이 때, 좌측의 측면말뚝 대비 우측의 측면말뚝에서 부재력이 더 크게 발생함을 확인하고, 우측 측면말뚝의 값을 분석하였으며, 시공단계는 최종 굴착단계와 4단 버팀보 해체 및 구조물/되메우기 단계(해석조건별 최대 전단력 및 휨모멘트 발생단계)를 기준으로 도시하였다(Fig. 10∼Fig. 11).
측면말뚝의 부재력은 유효응력 해석(Case 2) 조건에서 가장 크게 나타난 반면, 버팀보의 압축력은 압밀 해석(Case 3), 유효응력 해석(Case 2), 전응력 해석(Case 1)의 순으로 나타났다. 측면말뚝 변위의 경우 각각 전응력 해석(Case 1)은 4단 버팀보 해체 및 구조물/되메우기 단계, 유효응력 해석(Case 2)은 4단 굴착단계, 압밀 해석(Case 3)은 5단 버팀보 해체 및 구조물/되메우기 단계 이후에서 허용변위(0.2%H)를 초과하였다.
4.4 해석방법별 결과 비교
각 해석방법과 조건별 결과를 토대로 측면말뚝 및 버팀보에 대한 발생 부재력을 비교하였다(Table 12). 측면말뚝의 전단력과 버팀보의 축력은 탄소성해석에서 크게 예측되었고, 측면말뚝의 휨은 단기 유효응력 해석(Case 2)에서 가장 큰 것으로 평가되었다. 또한, 측면말뚝의 변위는 탄소성보다는 유한요소해석에서 더 큰 것으로 나타났다. 이상과 같은 결과로부터 점성토와 사질토가 혼재하는 지반에서 조합형 Sheet Pile 공법을 적용하는 경우, 탄소성 해석과 단기 전응력 해석이 항상 보수적인 설계라는 인식은 오류를 범할 수 있다는 것을 알 수 있었다(Table 12). 따라서 필요시 독일 굴착위원회(EAB, 2006) 권장사항과 같이 단기 전응력, 유효응력 및 압밀해석 등 유한요소해석을 통해 상세 검토가 수행되어야 함을 본 연구로부터 알 수 있었다.
Table 12.
Comparison of Elasto-Plastic and FEM Analysis Results
5. 결 론
본 연구에서는 사질토와 점성토가 혼재하는 해안 매립지반에서 조합형 Sheet Pile 벽체의 거동을 평가하고자 관련 설계법을 고찰하였고, 탄소성 해석과 유한요소해석 결과로부터 흙막이 구조물의 거동을 예측하여 다음과 같은 결과를 획득하였다.
(1) 조합형 Sheet Pile 공법의 형태(Built up, Interlocking, Welding) 및 해석방법(엄지말뚝법, 연속벽법)에 따라 흙막이 가시설의 예측 거동이 상이함을 탄소성 해석으로부터 확인하였다. 측면말뚝에 대한 엄지말뚝 해석법과 연속벽체 해석법의 결과, 연속벽체 해석법이 더 보수적인 결과를 예측하였다. 또한, 추후 이에 대한 설계시 주의 및 실증 연구가 필요함을 알 수 있었다.
(2) 탄소성 해석과 조합형 Sheet Pile 공법의 최대 부재력을 토대로 각 부재별 응력비(발생/허용)를 분석하면 측면말뚝의 경우 휨, 버팀보의 경우 조합응력에서 최대값을 나타내었다. 또한, 측면말뚝의 응력비로부터 Sheet Pile의 안정성은 휨에 의해 지배됨을 알 수 있었다.
(3) 유한요소해석 결과로부터 측면말뚝의 부재력은 유효응력 해석(Case 2) 조건에서 가장 크게 나타난 반면, 버팀보의 압축력은 압밀 해석(Case 3), 유효응력 해석(Case 2), 전응력 해석(Case 1)의 순으로 크게 나타났다. 측면말뚝 변위의 경우 압밀해석(Case 3)에서 최대값이 예측되었고, 전응력 해석(Case 1), 유효응력 해석, 압밀 해석(Case 3)별로 각각 다른 단계에서 허용기준(0.2%H)을 상회하였다.
(4) 탄소성과 유한요소해석의 측면말뚝 및 버팀보에 대한 부재력을 비교한 결과, 측면말뚝의 전단력과 버팀보의 축력은 탄소성해석에서 크게 발생하였고, 측면말뚝의 휨은 단기 유효응력 해석에서 크게 발생되었다. 또한, 측면말뚝의 변위는 탄소성보다는 유한요소해석에서 더 큰 것으로 나타났다.
(5) 본 연구로부터 사질토와 점성토가 혼재하는 지반에서의 굴착시 탄소성 해석과 단기 전응력 해석이 보수적인 설계라는 인식은 오류를 범할 수 있다는 것을 알았고, 필요시 단기 및 장기 안정성에 대한 유한요소해석을 통해 상세 검토가 수행되어야 함을 확인하였다.