1. 서 론
2. 한계상태설계법
2.1 하중저항계수설계법
2.2 목표신뢰도지수 및 목표파괴확률
2.3 비숍 간편법 한계상태함수식
3. 경사식 방파제 원호활동의 설계 사례 소개 및 신뢰성분석 물성 불확실성 가정
4. 신뢰성 분석 및 계수 산정 방법
5. 신뢰성해석 결과 및 하중 및 저항계수
5.1 상시 조건에서의 경사식 방파제 최적 하중 및 저항계수 계산
5.2 지진시 조건에서의 경사식 방파제 최적 하중 및 저항계수 계산
5.3 경사식 방파제 상부공 한계상태설계기준(안)
6. 결 론
1. 서 론
전 세계적으로 토목구조물 중 주요한 구조물을 위주로 확률에 근거한 설계법이 도입되고 있다. 하중저항계수설계법(Load and Resistance Factor Design; LRFD) 또는 Eurocode가 대표적이며, 대부분의 선진국(유럽, 미국, 일본)들은 확률론적인 설계법을 적극적으로 도입하고 있다(AASHTO, 2018; ECS, 1994).
또한 기존에는 확률론적인 설계법이 파괴시 피해규모가 큰 댐 구조물 등과 같은 대형구조물 위주로 진행된 반면 최근에는 하부기초, 사면, 옹벽 등의 다양한 지반구조물에 대하여 한계상태설계법이 개발되어 도입되고 있는 추세이다(Foye et al., 2006). 하지만 사람이 인위적으로 만드는 콘크리트, 강재 등을 다루는 구조물과 비교하여 지반구조물은 흙과 암에 대한 강도 및 특성 평가가 어렵다는 단점이 있다. 지반은 오랜 시간 동안의 자연 및 환경의 변화를 반영하여 형성되기 때문에 지역에 따른 공간적과 시간적인 변동성이 크다(Fenton, 1990; Kim, 2008). 대규모 구조물의 경우, 지반조사의 범위도 넓어지기 때문에 지반 정수의 변동성이 증가하여, 이를 분석하기에는 많은 어려움이 따르고 있다(Cherubini, 1997).
방파제의 신뢰성분석에 대한 연구는 제한적으로 수행되어 왔으며 국내에서는 대표적으로 Kim and Suh(2018)가 레벨 1∼3의 방법으로 피복블럭과 케이슨의 수평활동에 대한 신뢰성분석이 있다. 해당 연구에서 피복블럭과 케이슨의 손상 전 파괴확률은 허용되는 기준값인 목표파괴확률보다 높게 발생하여 제가 안전하게 설계되지 않았음을 확인하였다. 이후 보강된 방파제의 파괴확률은 목표 파괴확률값보다 낮았으며, 이를 통해 보강 후 방파제가 안정되었음을 확인하였다.
일본 해양구조물 기준(Japanese Standards for Coastal Structure)에서는 고다 파압(Goda, 1974)과 비숍 절편법(Bishop, 1955)을 이용하여 방파제의 안정성을 분석하도록 제시하였다. 다양한 조건에 대하여 몬테카를로 시뮬레이션을 이용하여 분석한 결과, 대부분 지반의 파괴가 가장 파괴확률이 높은 것으로 나타났다. Christiani(1997)은 경사식 방파제 설계시 다양한 파괴모드(전도, 수평활동, 지지력)에 대하여 복합 파괴에 대한 신뢰성 연구를 수행하였고, Takagi et al.(2011)은 기후변화로 인해 발생가능한 풍속 상승, 파고 증가 등을 고려하여 방파제의 안정성과 수평활동에 대한 영향을 확률론에 기반한 설계에 반영하였다.
본 연구에서는 경사제 방파제의 원호활동에 대한 하중저항계수법(LRFD)을 개발하였다. 이를 위해 Bishop 간편법(Bishop, 1955)을 이용하여 활동파괴모드를 정의하였고, 지반 정수의 공간적인 변동성은 과거의 문헌 연구 자료와 일본의 해양항만구조물 설계에 반영된 값을 참고하여 결정하였다.
2. 한계상태설계법
2.1 하중저항계수설계법
일반적으로 북미의 대표적인 한계상태설계법은 AASHTO에서 개발된 LRFD 형식이다. 식 (1)은 극한한계상태(Ultimate limit state)에 대한 AASHTO 설계법을 나타낸다.
| $$\phi\;R_n\geq\sum(LF_i)Q_{n,i}$$ | (1) |
여기서, ϕ는 저항계수, Rn은 공칭저항값, LFi는 i 종류의 공칭하중값인 Qn,i에 대한 하중계수이다.
AASHTO에서 제시한 LRFD의 경우, 하중 종류별 불확실성을 반영하여 다른 하중계수를 제시한 것이 특징이다. 극한한계상태는 풍속과 차량 등의 조건을 세분화하여 다른 하중 계수를 제시 한다. 하지만, 해양 구조물의 하중 특성을 반영하고 하중 종류에 따라 제시된 하중계수는 현재 없는 실정이다. 또한, 지역마다 해양 구조물에 작용하는 환경하중이 많이 다르기 때문에 전 세계적으로 사용할 수 있는 설계코드를 제시하기는 어렵다.
따라서 본 연구에서는 일본 해양항만구조물 설계(Overseas coastal area development institute of Japan, 2018), Technical Standards and Commentaries for Port and Harbor Facilities in Japan에서 사용되는 하중저항계수설계법 형식을 기반으로 경사식 방파제의 LRFD를 개발하였다. 일본 해양항만구조물 설계에서 제시하는 극한한계상태식은 식 (2)와 같다.
| $$(\gamma_R)R_n\geq(\gamma_Q)Q_n$$ | (2) |
여기서, γR과 γQ는 공칭총저항 Rn과 공칭총하중 Qn에 대한 저항 및 하중 계수이다.
일본 해양항만구조물 설계기준의 LRFD와 AASHTO LRFD 설계기준을 비교하면 일본 해양항만구조물 설계기준의 경우, 하중 종류에 관계없이 같은 하중계수를 사용한다는 것이다. 따라서 일본 해양항만구조물 설계기준에서 제시하는 하중계수 γQ와 저항계수 γR의 비(γQ/γR)는 등가안전율로 간주 될 수 있다. 하지만, 일본항만구조물 설계기준에서의 γQ/γR비는, 기존의 허용안전응력설계법(Allowable stress design)에서 사용되는 안전율과 비교하면, 목표파괴확률에 근거하여 제시된 하중계수 γQ와 저항계수 γR라는 차이를 보인다는 차별성이 있다.
2.2 목표신뢰도지수 및 목표파괴확률
하중저항계수설계법의 경우 목표신뢰도지수(또는 목표파괴확률)을 기반으로 하중 및 저항계수를 제시한다. 합리적인 목표신뢰도지수를 결정해야 하지만 이는 구조물의 중요도, 파괴 시 예상되는 인적 물적 피해정도, 내구수명, 다른 구조물과의 연계성 등을 종합하여 고려해야 한다. 경사식방파제의 원호활동에 대한 하중 및 저항계수를 산정하기 위해서는 앞에서도 언급한 바와 같이 대표적인 절편법인 비숍 간편법을 사용하였다. 이는 일반적인 토목구조물인 사면에 대한 안정성을 평가하는데 사용되는 해석 방법이다. 또한, 해양구조물에 대한 목표신뢰도지수 또는 목표파괴확률을 제시한 연구가 없기 때문에, 본 연구에서는 기존에 제시된 사면의 적정 허용파괴확률을 경사식방파제의 목표신뢰도 지수를 결정하는 참고값으로 사용하였다. Table 1은 Santamarina et al.(1992)가 제시한 사면의 적정 허용파괴확률이다.
Table 1. Acceptable probability of failure for slopes (modified after Santamarina et al., 1992)
경사식 방파제의 목표신뢰도지수의 경우, 발주처와 전문가의 의견 수렴에 의하여 결정되어야 한다. 경사식 방파제 구조물의 파괴가 발생할 경우, 직접적인 인명 피해가 발생할 가능성은 적다. 하지만 파도의 영향으로 근접 지역에 피해를 줄 수 있기 때문에 인구 밀집도 또는 시설의 밀도 등과 같은 지역 특성에 따라 합리적인 목표파괴확률 또는 목표신뢰도지수를 결정하는 것이 중요하다. 따라서, 본 연구에서는 목표신뢰도지수를 넓은 범위로 설정하고자하며, 목표신뢰도지수 2.0, 2.5, 3.0, 3.5에 대한 하중 및 저항 계수를 제시하였다.
2.3 비숍 간편법 한계상태함수식
절편분할법은 사면의 가상 파괴면 내부의 토체를 연직으로 분할하여 각 절편에 대한 힘 및 전체 활동 모멘트의 평형을 고려하여 사면 안정해석을 하는 방법이다. 비숍 간편법에 의한 안정해석법은 절편의 수직면내에 활동하는 수직방향 전단력과 수평력을 고려한 산정식으로 해석을 한다. 한계상태함수식 G(x)는 실제의 경사식 방파제 안정성 계산에서는 수직방향 전단력이 평형을 이루고 있다고 가정하여 수직방향 전단력을 무시하고 식 (3)과 같이 정의한다.
| $$G(x)=\sum_{}^{}\frac{c_kb+(W_k+q_k-u_k)\tan\phi_k}{\cos\alpha(1+\tan\alpha\tan\phi_k)}-\sum_{}^{}(W_k+q_k)\sin\alpha$$ | (3) |
여기서, ck는 점성토지반인 경우에는 비배수 전단강도의 특성치, 사질토지반인 경우에는 배수조건에서 겉보기 점착력의 특성치(kN/m2), b는 각 절편의 폭(m), Wk은 절편 유효 중량의 특성치(흙의 중량, 수면 아래에서는 수중 단위체적 중량)(kN/m), qk는 절편 상부에서 수직하중의 특성치(kN/m), uk는 절편 하부에 작용하는 평균 수압(kN/m), ϕk는 점성토지반인 경우에는 0, 사질토지반인 경우에는 배수조건에서 내부마찰각의 특성치(°)이다.
3. 경사식 방파제 원호활동의 설계 사례 소개 및 신뢰성분석 물성 불확실성 가정
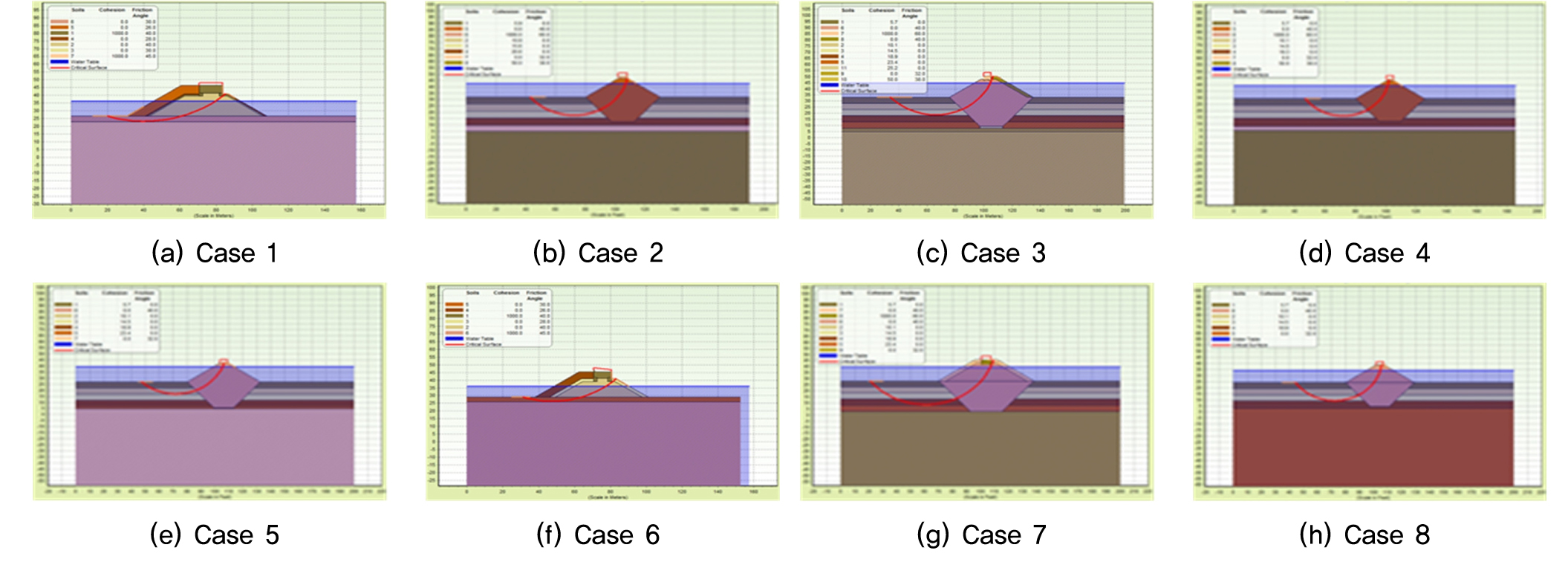
본 연구에서는 제주도와 거제도 지역에 8개의 경사식 방파제를 대상으로 상시와 지진시에 대한 설계 자료를 분석하였다. 연구대상 8개 항의 상부공 및 지반 조건을 반영한 설계자료를 바탕으로 신뢰성 해석을 수행하였고, 현행 설계법으로 시공된 경사식 방파제의 원호활동에 대한 하중 및 저항계수를 산정하였다. Fig. 1은 사면해석 프로그램인 STABL을 이용하여 해석한 연구대상 8개 항의 방파제 형상 및 원호파괴 활동면을 나타낸다.
이때, 경사식 방파제 단면은 다양한 하부 지층과 상부공 등으로 나뉘며 각 층에 대해서 점착력, 마찰각, 단위중량은 불확실성을 가지는 변수로 취급한다. 이에 대한 설계변수 변동성은 지역 또는 지층분할 조건에 따라 달라지기 때문에 이를 객관적으로 정량화하기 어렵다. 또한 상치 콘크리트 상부에 작용하는 재하량과 지진 해석시 적용하는 지진계수에 대해서도 불확실성을 가지는 변수이기 때문에 이에 대한 편향계수와 변동계수도 결정해야 한다. 일본 해양항만구조물 설계에서는 경사식 방파제 설계변수에 대하여 Table 2와 같이 가정하고 있다.
Table 2. Uncertainties of soil parameters, traffic load, and horizontal seismic coefficient of pseudostatic approach from Technical Standards and Commentaries for Port and Harbour Facilities in Japan (The overseas coastal area development institute of Japan, 2018) for mound breakwater reliability analysis
8개의 경사식 방파제에 대하여 신뢰성 분석을 한 결과, 계산된 신뢰성지수가 다소 높게 측정되었다. 지역에 따라 강도정수(점착력과 마찰각), 지진계수 등의 변동성의 차이가 발생할 수 있기 때문에 Table 2에 제시된 강도정수와 지진계수를 보다 더 큰(보수적인) 값을 Table 3과 같이 가정하여 해석을 수행할 필요가 있다. 따라서 안정성 해석에 민감하고 중요한 강도정수의 변동계수(표준편차/평균 비)를 0.04에서 0.10으로 증가시키고, 지진계수도 0.05에서 0.10으로 상향하였다(Table 3). 하지만 보수적으로 가정한 높은 강도정수와 지진계수의 변동성은 다소 비현실적으로 저항계수를 낮출 수 있기 때문에 신중한 가정이 필요하다.
Table 3. Uncertainties of soil parameters, traffic load, and horizontal seismic coefficient of pseudostatic approach assumed in this study for mound breakwater reliability analysis
4. 신뢰성 분석 및 계수 산정 방법
지층의 지반정수, 단위중량, 외력, 지진력 등의 각 불확실성을 고려한 사면에 대하여 가장 취약한 가상파괴면을 찾아야 하는 원호활동 안정성 평가의 복잡한 과정 때문에 신뢰성 해석 또한 어렵다. 따라서 경사식 방파제 원호활동에 대한 신뢰성해석은 Level Ⅲ 방법인 Monte Carlo Simulation을 통해 신뢰성지수를 계산하였으며, 하중 및 저항계수를 산정할 때는 대표적인 Level Ⅱ 방법인 First-Order Reliability Method(FORM)를 사용하였다. 최적 하중 및 저항계수는 다음과 같은 절차에 따라 결정된다.
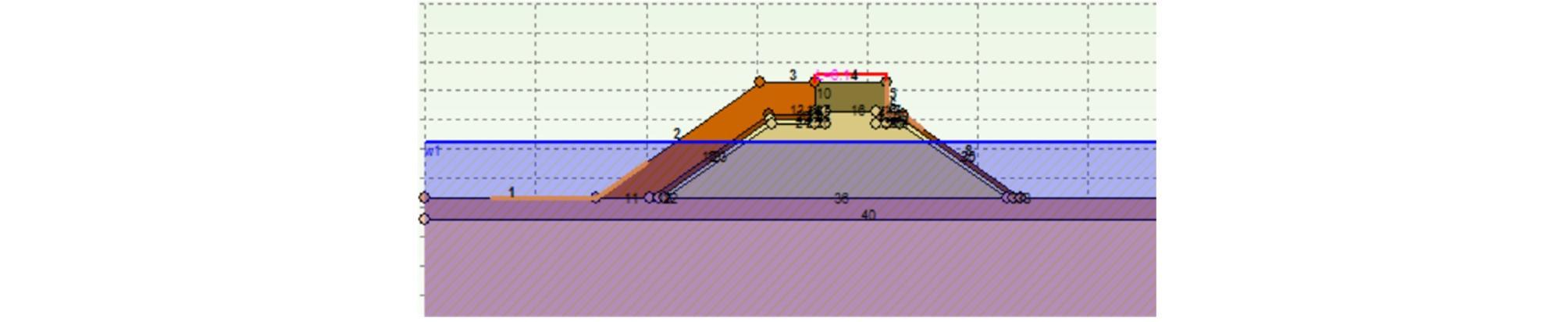
(STEP 1) 상치 콘크리트를 포함한 각 지층의 강도정수, 단위중량, 외력, 지진력 등의 불확실성을 반영하여 난수를 발생시킨 후 사면해석프로그램에 입력한다(Fig. 2).
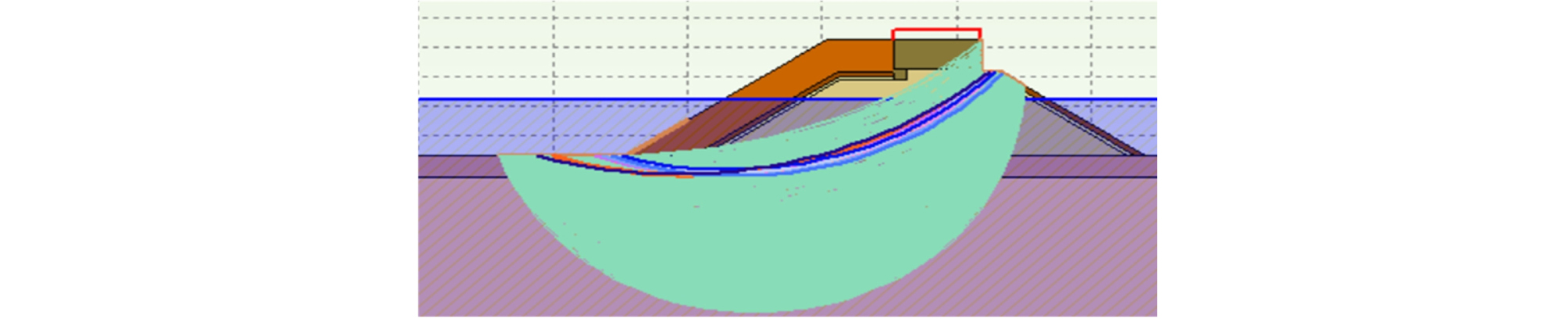
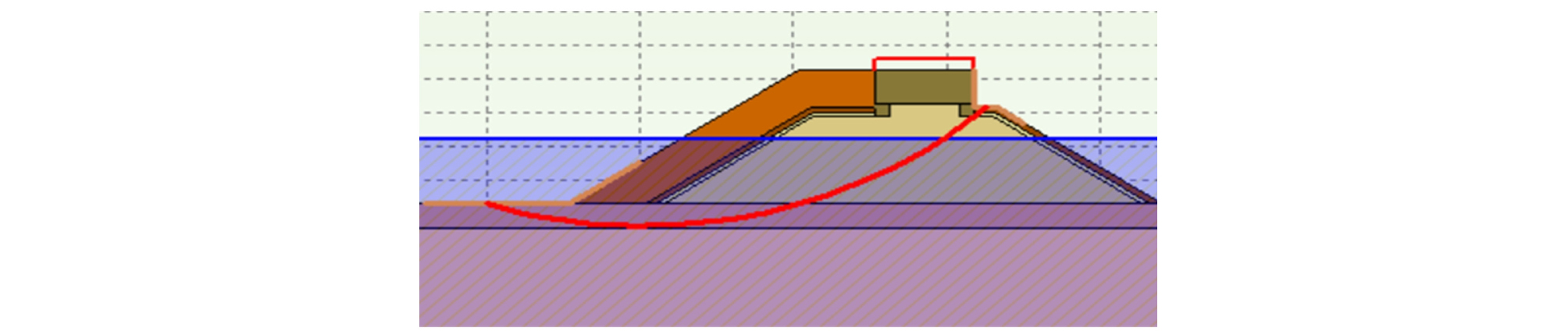
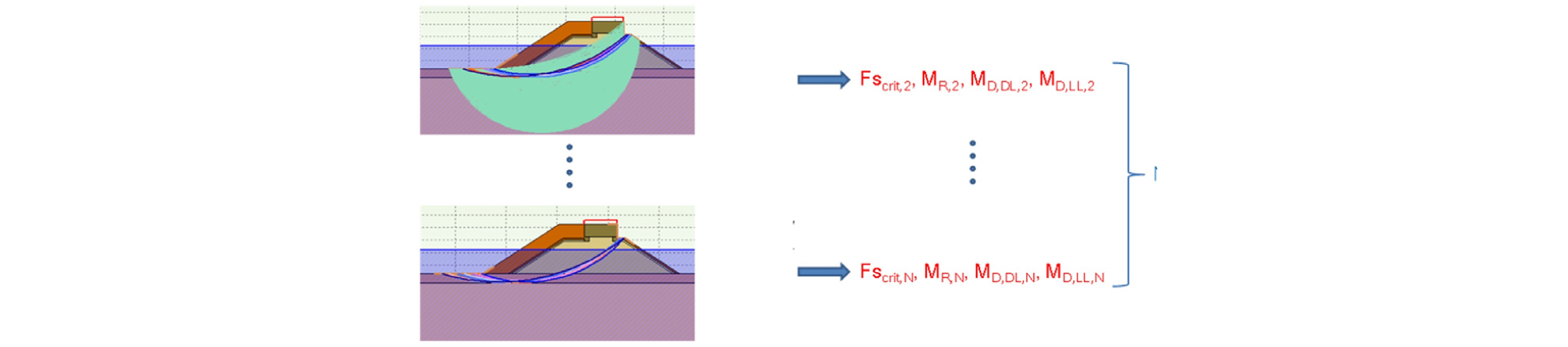
(STEP 2) 충분히 많은 가상 파괴면을 발생시켜 그 중, 가장 불안한(저항모멘트/하중모멘트 비가 가장 작은) 가상 파괴면을 찾고, 이때의 저항모멘트와 하중모멘트를 분리하여 계산하여 저장한다(Figs. 3 and 4).
(STEP 3) 몬테카를로 시뮬레이션을 수행하기 위하여 (STEP 1)∼(STEP 2)과정을 계산된 신뢰성지수(파괴확률)가 수렴할 때까지 반복한다(Fig. 5).
(STEP 4) Monte Carlo Simulation으로부터 저장된 각 simulation별 저항모멘트/하중모멘트 비, 하중모멘트와 저항모멘트를 저항모멘트/하중모멘트 비의 오름차순으로 정리한다. 전체 simulation 회수(N) 대비 파괴 회수(n; 저항모멘트/하중모멘트 비가 1보다 작은 회수)를 계산하여 파괴확률을 계산하고, 이를 통해 등가 신뢰성지수를 산정한다(Fig. 6).
(STEP 5) 하중모멘트와 저항모멘트의 불확실성 및 상관성을 평가하고, 상관관계를 반영한 FORM을 이용하여 최적 하중 및 저항계수(γ*Q와 γ*R)를 산정한다.
| $$\gamma\ast_Q=\frac{Q_{LS}}{Q_n},\;\gamma\ast_R=\frac{R_{LS}}{R_n}$$ | (4) |
여기서, Rn과 Qn는 저항과 하중의 공칭값(설계값)이며, RLS과 QLS는 확률적으로 파괴확률이 가장 높은 한계상태의 저항과 하중값이다.
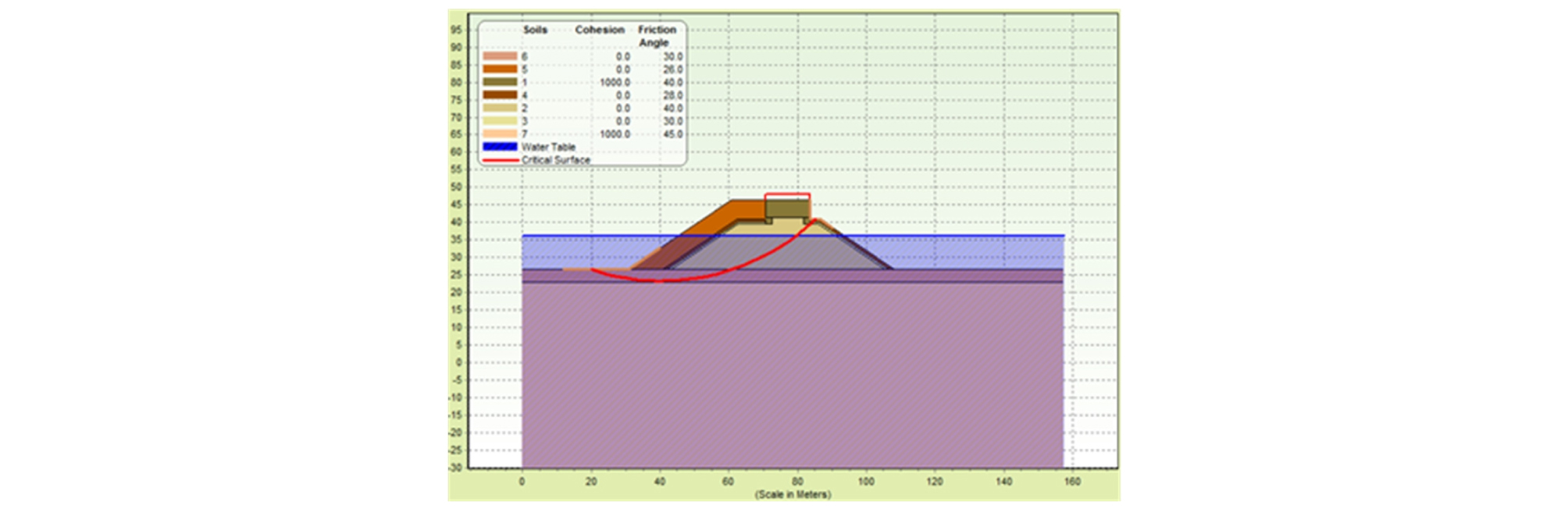
대표적인 경사식 방파제의 신뢰성 해석 예시는 제주도에 위치한 OO 남방파제이며 해당 조건은 Fig. 7과 같다. 지반정수, 단위중량, 외력의 불확실성은 Table 2의 값으로 가정하였다. 앞서 제시된 절차를 따라 결정론적인 해석을 한 결과, 활동모멘트의 합은 3,591.556kNm/m/m이였으며, 이중 토체에 의한 활동모멘트는 3,514.138kNm/m/m, 상부외력하중에 의한 활동모멘트는 77.418kNm/m/m의 결과를 보였다. 저항모멘트는 8,244.750kNm/m/m으로 안전율을 2.296이였다.
같은 조건으로 몬테카를로 시뮬레이션을 통하여 신뢰성 분석(경사식 방파제의 신뢰도지수 또는 파괴확률 계산)을 해 본 결과, 계산된 신뢰성지수는 10.86이였다. 결과적으로 허용최소안전율이 1.3인 것에 비하여 계산된 안전율이 2.296이므로 최종 설계에서는 경사식 방파제 원호활동에 대해서는 많이 보수적으로 설계된 것을 확인하였다. 또한 목표신뢰성지수가 일반적으로 4.0을 넘지 않는데, 계산된 신뢰성지수가 10.86인 것은 파괴확률이 아주 낮음을 의미한다.
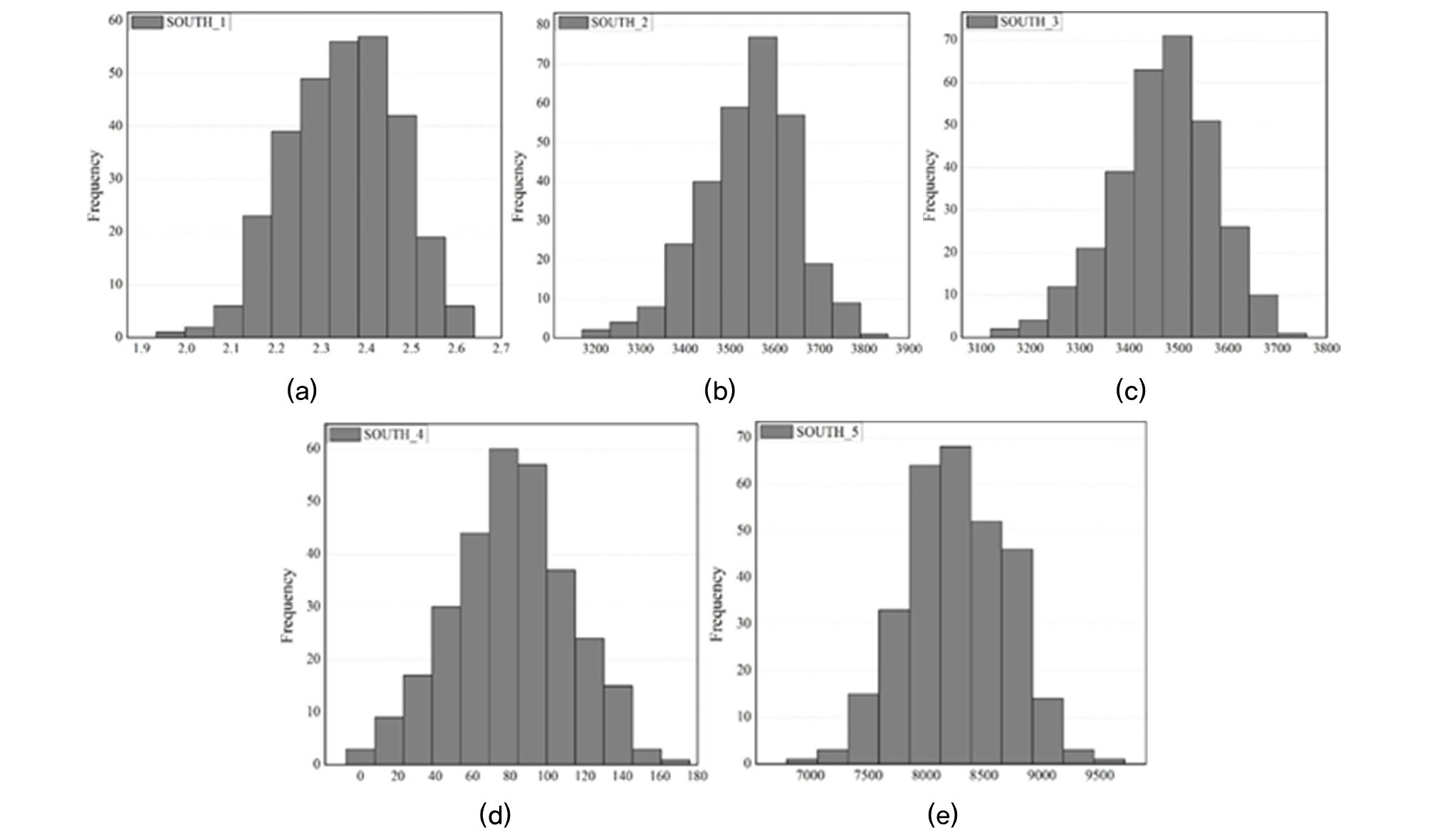
제주도에 위치한 OO 남방파제의 몬테카를로 시뮬레이션 결과로부터 도출된 안전율 분포, 전체 활동모멘트 분포, 토체에 의한 활동모멘트 분포, 외력하중에 의한 활동모멘트 분포, 저항모멘트의 분포를 Fig. 8과 같이 도식화 하였다. 식 (4)를 이용하여 목표 신뢰성 지수 2.5에 대하여 하중과 저항의 상관성을 반영하여 LRFD의 최적 저항계수(γ*R)와 하중계수(γ*Q)를 산정하였다. 그 결과, LRFD 형식의 최적 하중 및 저항계수는 각 1.04과 0.98로 계산되었다.
5. 신뢰성해석 결과 및 하중 및 저항계수
5.1 상시 조건에서의 경사식 방파제 최적 하중 및 저항계수 계산
식 (4)를 이용하여 상시 조건에 대하여 Table 2와 Table 3에 제시된 경사식 방파제 관련 지반 전단강도, 단위중량, 재하량 등의 불확실성을 반영하여 최적 하중 및 저항계수를 산정하였다(Table 4와 Table 5).
Table 4는 Table 2에 제시된 불확실성을 반영하여 구해진 하중과 저항 통계값과 하중과 저항의 상관성을 반영한 최적 하중 및 저항 계수이다. 하중과 저항의 상관성은 크게 보면 가장 취약한 원호파괴형상과 지반정수 중에 마찰정수(마찰각)의 전체 저항에 대한 기여도에 따라 달라진다. 대부분 같은 원호파괴형상에 대하여 하중과 저항 모멘트를 구하기 때문에 높은 상관성을 가지게 된다.
Table 4. Optimal load and resistance factors of mound breakwater against circular failure for different target reliability indices for eight design cases under ordinary condition (non-seismic condition) using uncertainties in Table 2 and correlation between driving and resisting moments
Table 5에 정리된 하중 및 저항 계수는 Table 3에 제시된 불확실성을 반영하여 계산하였다. Table 4에서 최적 하중 및 저항 계수를 구할 때 반영한 하중과 저항의 상관성을 반영하지 않고 Table 5의 최적 하중 및 저항 계수를 구하였다. 이는 하중과 저항의 상관성을 반영하지 않을 경우, 아주 보수적인 최적 하중 및 저항 계수 조합이 나오는 것을 보여주기 위함이다. 목표신뢰성지수(βT)는 2.0, 2.5, 3.0, 3.5로 다양한 값으로 설정하였으며, 각 설계 사례별로 하중 계수는 큰 차이를 보이지 않았으나, 저항계수는 다소 큰 차이를 보였다.
Table 5. Optimal load and resistance factors of mound breakwater against circular failure for different target reliability indices for eight design cases under ordinary condition (non-seismic condition) using uncertainties in Table 3 assuming no correlation between driving and resisting moments
상시 해석의 결과(Table 4와 Table 5)에서 볼 수 있듯이, 강도정수와 지진계수의 변동성(변동계수)을 0.1로 높일 경우, 일반적으로 최적 하중 계수의 값은 증가하고 최적 저항 계수의 값은 감소하는 것을 볼 수 있다. 이렇게 강도정수와 지진계수의 변동성을 크게 할 경우 비합리적으로 낮은 저항계수가 도출될 수 있다. 따라서, 합리적으로 판단되는 Table 2에 제시된 변동성을 반영하여 최적 하중 및 저항계수를 Table 6과 같이 제시하였다. 최종 최적 하중 및 저항 계수는 Table 4의 제시된 최적 하중 평균값이다.
Table 6. Finally determined optimal load and resistance factors of mound breakwater against circular failure for different target reliability indices under ordinary condition from analyses of eight design cases
| Target reliability index βT | Optimal resistance factor γ*R | Optimal load factor γ*Q |
| 2.0 | 0.96 | 1.03 |
| 2.5 | 0.95 | 1.04 |
| 3.0 | 0.93 | 1.04 |
| 3.5 | 0.91 | 1.04 |
5.2 지진시 조건에서의 경사식 방파제 최적 하중 및 저항계수 계산
지진시에 대해서도 경사식 방파제의 안정성을 검토하였다. Table 2에 제시된 지반정수, 재하량, 지진계수의 변동성을 반영하여 몬테카를로 시뮬레이션을 통하여 하중 및 저항 특성을 도출하였다. 이러한 하중 및 저항 특성을 반영(하중과 저항의 상관성도 반영)하여, 최적 하중 및 저항계수를 계산하였으며, 그 결과를 Table 7에 정리하였다.
상시 조건에서 최종 최적 하중 및 저항 계수를 구하는 방식과 같이, 지진시의 최종 최적 하중 및 저항 계수를 Table 8에 제시된 최적 하중 및 저항 계수의 평균값으로 결정하였다.
Table 7. Optimal load and resistance factors of mound breakwater against circular failure for different target reliability indices for eight design cases under seismic condition using uncertainties in Table 2 and correlation between driving and resisting moments
Table 8. Finally determined optimal load and resistance factors of mound breakwater against circular failure for different target reliability indices under seismic condition from analyses of eight design cases
| Target reliability index βT | Optimal resistance factor γ*R | Optimal load factor γ*Q |
| 2.0 | 0.94 | 1.01 |
| 2.5 | 0.92 | 1.01 |
| 3.0 | 0.90 | 1.01 |
| 3.5 | 0.88 | 1.02 |
5.3 경사식 방파제 상부공 한계상태설계기준(안)
상시와 지진시 경사식 방파제 원화활동에 대하여 한계상태식 (3)을 이용하여 안정성을 검토하였으며, 목표신뢰성지수 2.0∼3.5에 대하여 하중 및 저항계수를 Table 9와 같이 제안하였다. 일반적으로 하중 및 저항계수는 0.05단위로 제시하기 때문에, 계산된 하중 계수는 0.05 단위를 기준으로 올림하고, 계산된 저항계수는 0.05 단위로 절삭하는 것이 관례이다. 목표신뢰도지수 2.0과 2.5에 대해서는 상시와 지진시 최적 하중 및 저항 계수가 상이하지만, 0.05 단위 기준으로 하중 계수의 올림과 저항계수의 내림 처리를 한 결과 최종 제안 하중 및 저항 계수는 각각 1.05와 0.95로 결정되었다. 목표신뢰도지수 3.0과 3.5에 대해서도 같은 이유로 상시와 지진시에 대하여 최종 제안 하중 및 저항 계수는 각각 1.05와 0.90으로 제시한다.
Table 9. Final proposed load and resistance factors of mound breakwater against circular failure for different target reliability indices under both ordinary and seismic conditions from analyses of eight design cases
| Target reliability index βT | Optimal resistance factor γR | Optimal load factor γQ |
| 2.0, 2.5 | 0.95 | 1.05 |
| 3.0, 3.5 | 0.90 | 1.05 |
6. 결 론
본 논문에서는 경사식 방파제의 원호활동에 대한 하중 및 저항계수를 8개의 방파제 case에 대하여 계산하고, 그 결과를 토대로 다양한 목표신뢰도지수에 따른 합리적인 수준의 하중 및 저항계수를 제시하였다. 경사식 방파제의 원호활동의 경우, 경사제 자중의 규모, 점착력으로 인해 발생하는 저항력 비율이 신뢰성지수에 큰 영향을 미치며, 이러한 영향은 최종적으로 하중 및 저항계수에도 영향을 미치게 된다. 경사식 방파제의 원호활동에 대한 신뢰성지수는 강도정수의 변동성 및 하중과 저항의 상관성에 가장 큰 영향을 미치는데 이에 대한 합리적인 가정을 해야 한다. 상시와 지진시에 대한 경사식 방파제 원호활동에 대한 목표신뢰도지수에 따른 하중 및 저항계수는 같은 값으로 도출되었다. 이는 일반적으로 하중 및 저항 계수를 0.05단위로 제시하는 관례 때문에 발생한 값이며, 상시와 지진시의 각 목표신뢰도지수에 따른 최적 하중 및 저항계수는 차이를 보인 것을 확인하였다.
본 연구에서 허용응력설계법과 다르게 경험으로부터 도출된 안전율이 아닌 신뢰성분석으로부터 도출된 하중 및 저항 계수를 제시하였다는 점에서 공학적으로 의미가 있다. 하지만 이번 연구에서 개발한 경사제 방파제 원호활동에 대한 하중저항계수설계법에서는 제한된 구조물 사례로부터 도출된 최적 하중 및 저항계수를 산정하였기 때문에, 실제 설계에 반영하기 위해서는 더 많은 설계 자료를 토대로 지반 정수의 불확실성 데이터를 확보하여야 한다.