1. 서 론
2. 속도의 PSI
2.1 속도의 PSI 정의
2.2 속도의 PSI와 침하량 상관관계
3. 속도의 PSI 산정 및 거동 분석
3.1 속도의 PSI 산정
3.2 지속시간에 대한 속도의 PSI 거동
3.3 입력가속도 크기에 대한 속도의 PSI 거동
3.4 기존의 간편법(Sone et al., 2012) 산출식
4. 수치해석을 이용한 케이슨식 안벽의 내진안정성 평가
4.1 수치해석 개요
4.2 수치해석 모델
4.3 액상화 입력변수 산정
5. 해석결과
5.1 간편법과 수치해석 결과 비교 – 수평변위
5.2 보정계수 제안 – 수평변위
5.3 보정계수 적용 후 간편볍과 수치해석 결과 비교 – 수평변위
5.4 간편법과 수치해석 결과 비교 – 침하량
5.5 보정계수 제안 – 침하량
5.6 보정계수 적용 후 간편법과 수치해석 결과 비교 – 침하량
6. 활용방안 및 결론
6.1 활용방안
6.2 결론
1. 서 론
오늘날, 전체 글로벌 무역 중 해상 물동량 비중은 약 85%로 절대적인 비중을 차지하고 있다. 한국의 경우 수출입 물동량의 99.7%가 해운을 통해 처리되고 있으며, 그 중 석유와 중요 원자재 등은 100% 해운을 통해 수송되고 있다. 이토록 국가 유지 및 국제교역의 중추를 맡고 있는 해운업의 경쟁력 강화를 위해 각국의 정부는 해운산업 인프라 발전에 많은 투자를 하고 있다. 이에 따라 해안구조물의 안정성 문제 역시 대두되고 있다. 특히 한국의 경우 2017년 포항 지진(M5.2)으로 인한 영일만항 케이슨식 안벽의 피해가 관측된 이후 케이슨식 안벽구조물에 대한 내진성 조사의 필요성이 강조되고 있다. 케이슨식 안벽이란 자중과 저면의 마찰력에 의해 토압, 수압 등 외력에 대하여 저항하는 구조이며, 대형 컨테이너 선박의 계류를 목적으로 해안에 시공되는 구조물이다. 일반적으로 케이슨식 안벽의 상단부에는 화물의 하역을 위한 크레인이 설치된다. 케이슨식 안벽은 단단하고 무거우므로 선박의 충격에 대한 저항은 크지만, 지진에 취약하다는 단점이 있다. 지진 시 횡토압의 증가 혹은 기초지반 및 배후지반 액상화로 인해 케이슨식 안벽에 영구변형이 발생하게 된다. 안벽에 영구변형이 발생하면 선박의 접안 및 크레인 운영에 문제가 생기고, 이는 곧 해운업의 손실로 이어진다. 이러한 피해를 방지하기 위해서 지진으로 인해 케이슨식 안벽에 발생할 피해를 예측하고 그에 따른 내진 보강을 실시할 필요가 있다. 지진 시 구조물의 피해를 예측하는 방법으로는 2차원 유효응력 해석법과 모형시험 등이 존재한다. 하지만 이 과정들은 매우 복잡하여 많은 시간과 비용이 소요된다는 문제가 있다. 이러한 문제를 해결하기 위해 케이슨식 안벽구조물의 피해를 간단하고 빠르게 예측할 수 있는 간편법의 개발이 필요하다. 간편법을 이용한다면 지진에 취약한 시설을 빠르게 추출하여 위험도가 높은 시설부터 순차적으로 내진 보강을 실시할 수 있어 효과적으로 지진에 대비할 수 있다. 본 연구에는 속도의 PSI를 활용하여 지진 시 안벽의 피해를 빠르고 쉽게 예측할 수 있는 간편법 개발을 목표로 하였다.
2. 속도의 PSI
2.1 속도의 PSI 정의
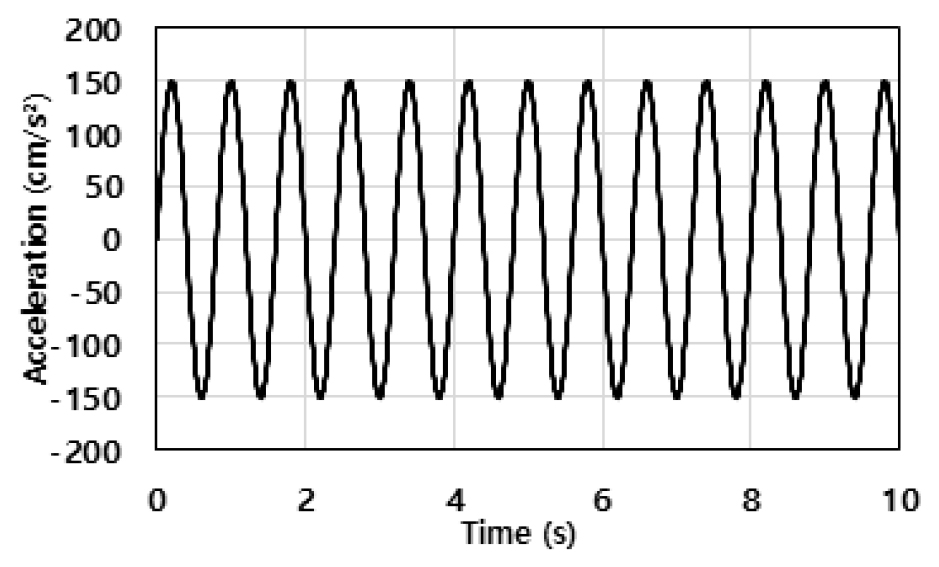
속도의 PSI(Power Spectral Intensity) 값은 지진 운동이 해안구조물의 변형량에 미치는 영향을 평가하는 지표 중 하나이며 Fig. 1(a)와 같은 가속도 파형을 시간에 대해 적분한 뒤 Fig. 1(b)와 같이 속도 파형으로 나타내며, 그 속도 파형의 제곱 적분값의 제곱근이 속도의 PSI이다. Fig. 1(c)와 같이 나타내어진다.
속도의 PSI의 식은 다음 식 (1)과 같다(Nozu and Iai, 2001).
여기서, 는 속도()를 나타낸다.
2.2 속도의 PSI와 침하량 상관관계
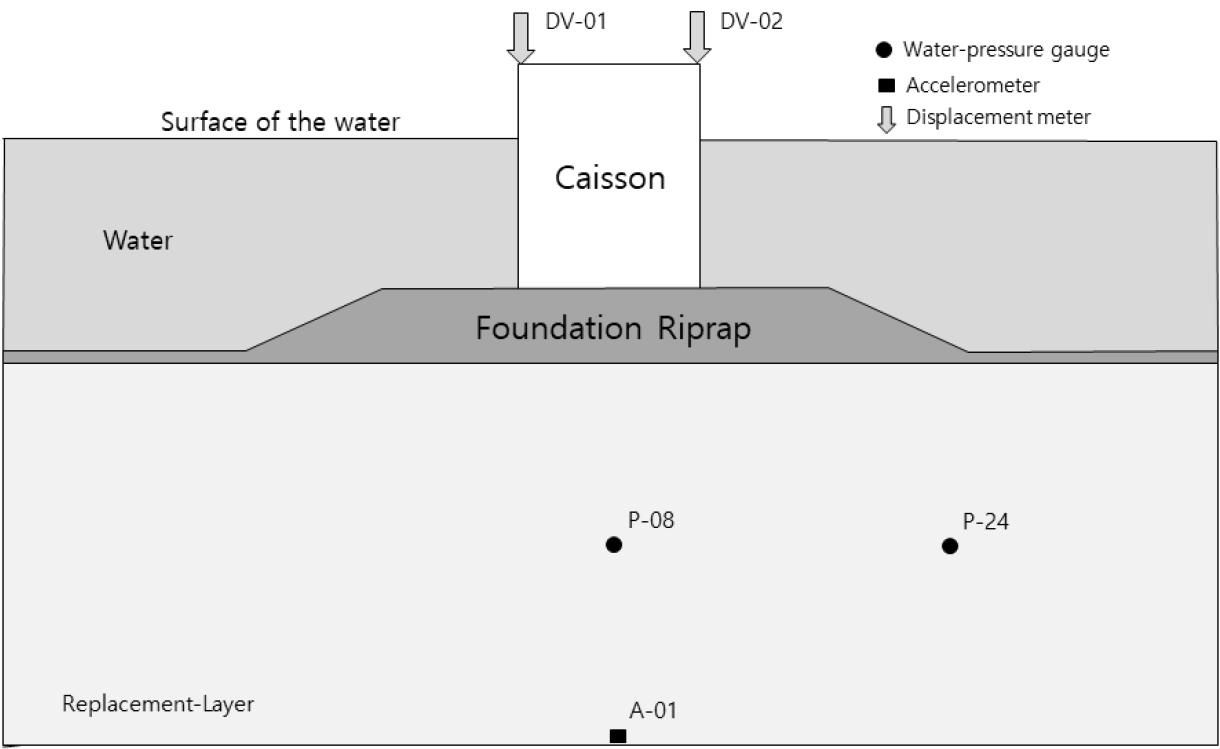
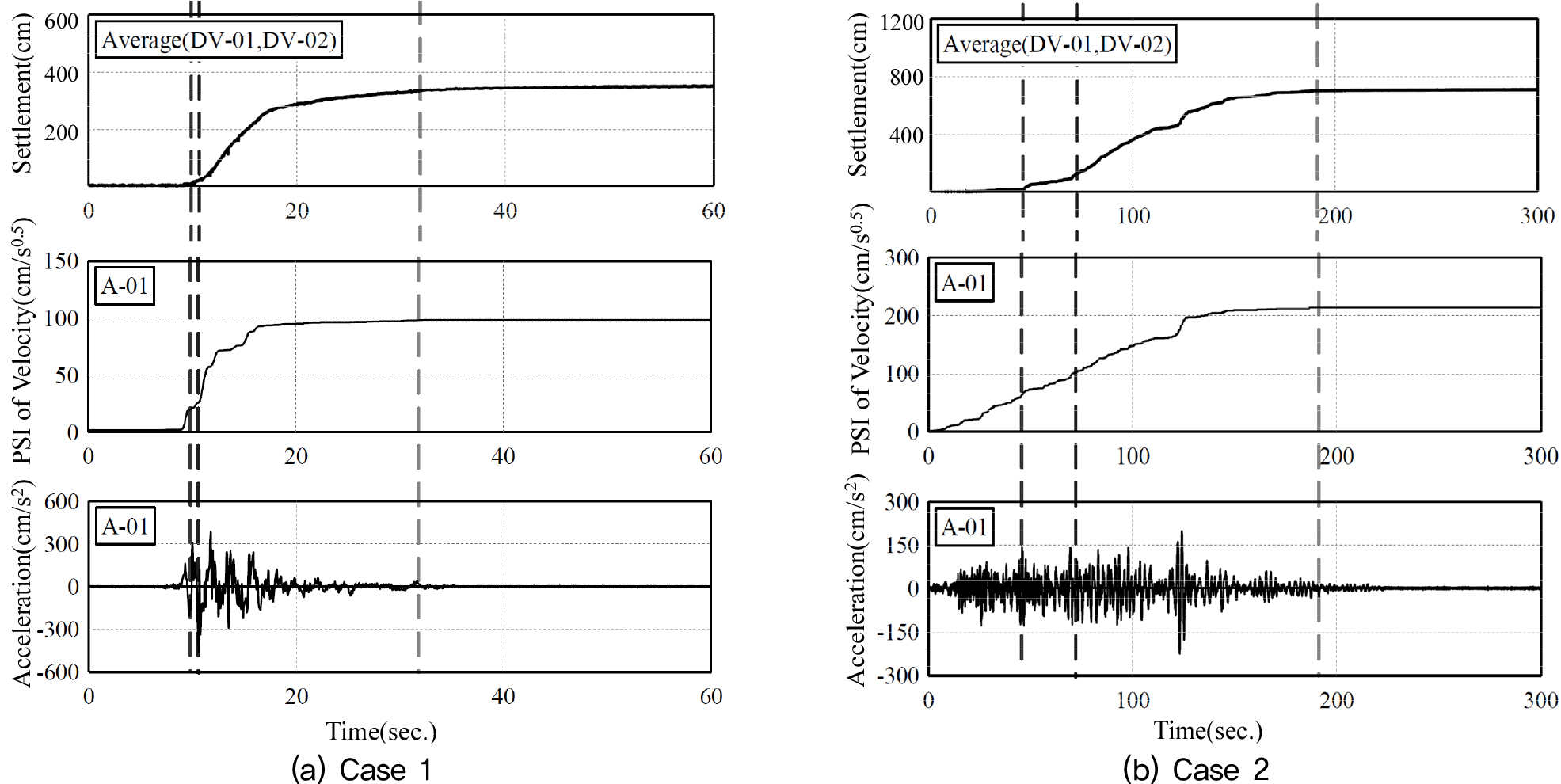
Fig. 2와 같이 1/20 축척의 중력식 방파제 모델의 진동대모형시험을 수행하였고(Ohya et al., 2013), Fig. 3은 모형시험을 통해 얻은 침하량, 속도의 PSI(), 그리고 지진가속도의 그래프이다. Case 1과 Case 2의 경우 모두 안벽의 침하량과 속도의 PSI의 거동이 서로 상당히 유사한 형태를 보이는 것을 확인할 수 있다.
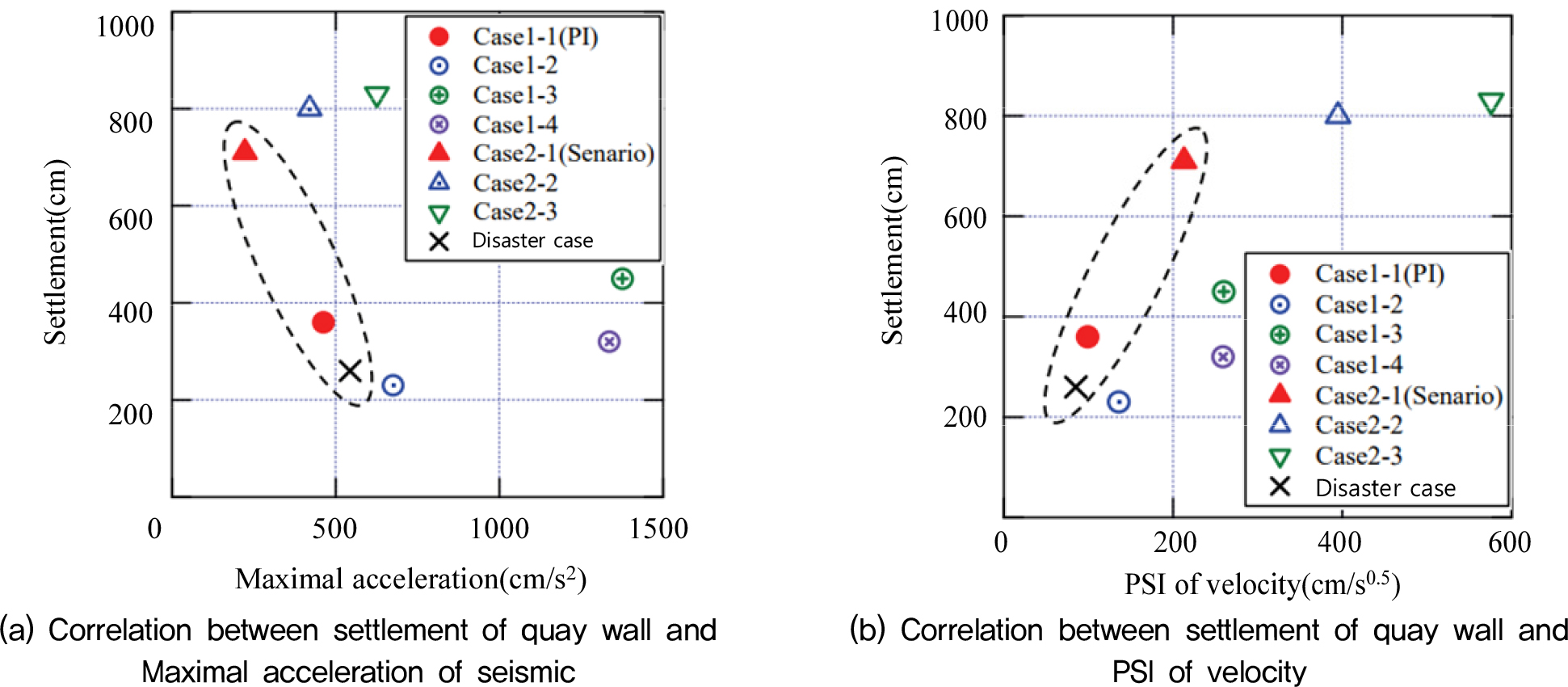
Fig. 4(a)에서는 입력 최대가속도와 케이슨 안벽의 침하량의 관계를 나타내고 있다. 일반적으로는 최대가속도가 증가할수록 침하량도 커질 것으로 판단된다. 하지만 최대가속도가 증가할수록 침하량은 작아지는 경향을 보이기도 한다. 반면에 Fig. 4(b)에서 속도의 PSI가 증가하면 케이슨식 안벽의 침하량도 같이 증가하는 것을 볼 수 있다(Ohya et al., 2013).
또한, Fig. 5는 입력 지진동의 최대가속도 및 최대속도, 가속도의 PSI 및 속도의 PSI와 안벽의 수평 잔류변위와의 상관관계를 나타낸 것이다. 그림에 보이는 것과 같이 속도의 PSI와 안벽의 잔류 수평변위의 상관관계가 액상화와 비액상화 지반에서 0.875, 0.903으로 가장 높은 것을 확인 할 수 있다(Nozu and Iai, 2001).
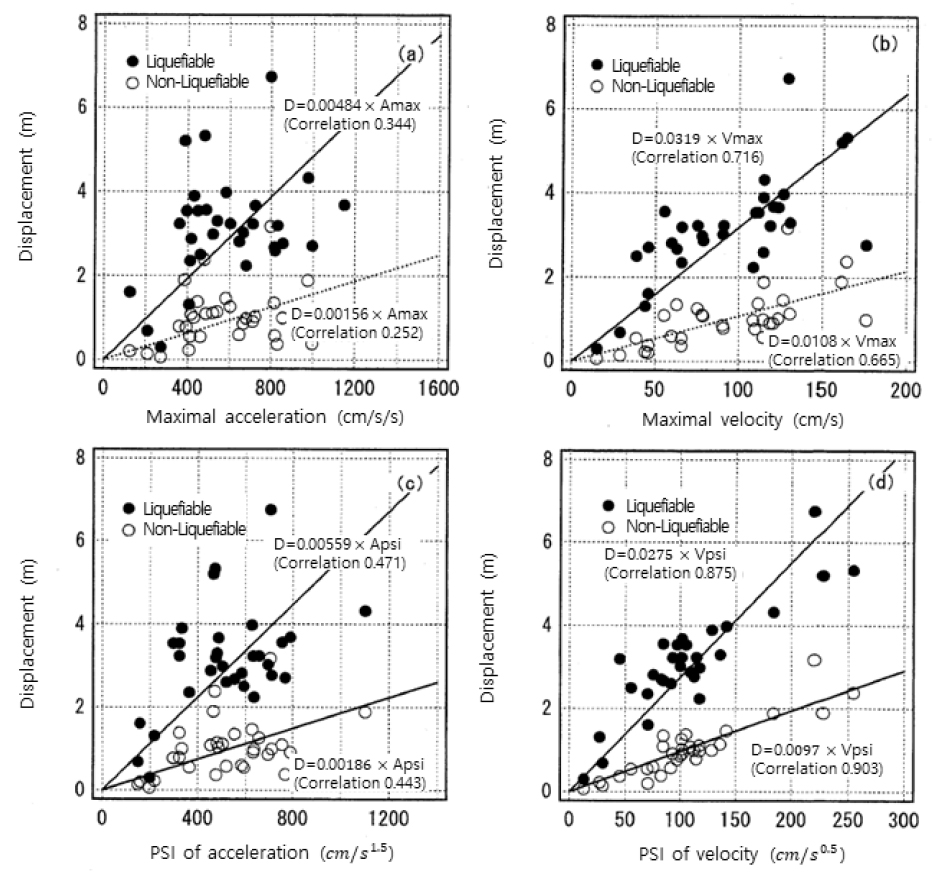
Fig. 5.
Relationship between PSI of maximum acceleration, maximum acceleration, PSI of velocity and horizontal displacement of quay walls (Nozu and Iai, 2001)
속도의 PSI는 지진 지속시간과 진동수의 영향에 대해 고려할 수 있으므로 해안구조물의 피해거동을 잘 모사할 수 있다. 특히 안벽구조물의 변위와 속도의 PSI의 상관관계가 높은 것으로 확인되었다. 따라서 지진 시 케이슨식 안벽의 변위량을 예측하기 위해 속도의 PSI를 활용하는 것이 적절하다고 판단된다.
3. 속도의 PSI 산정 및 거동 분석
3.1 속도의 PSI 산정
본 연구에서는 앞서 언급하였던 속도의 PSI 산출식을 통해 Matlab 프로그램으로 지속시간과 입력가속도 크기별 속도의 PSI를 Table 1과 같이 나타내었다.
Table 1.
PSI of velocity by sustainment time and input acceleration
여기서 지속시간은 초(sec)단위이고 입력가속도(Gal)는 ()이며, 속도의 PSI는 ()이다.
3.2 지속시간에 대한 속도의 PSI 거동
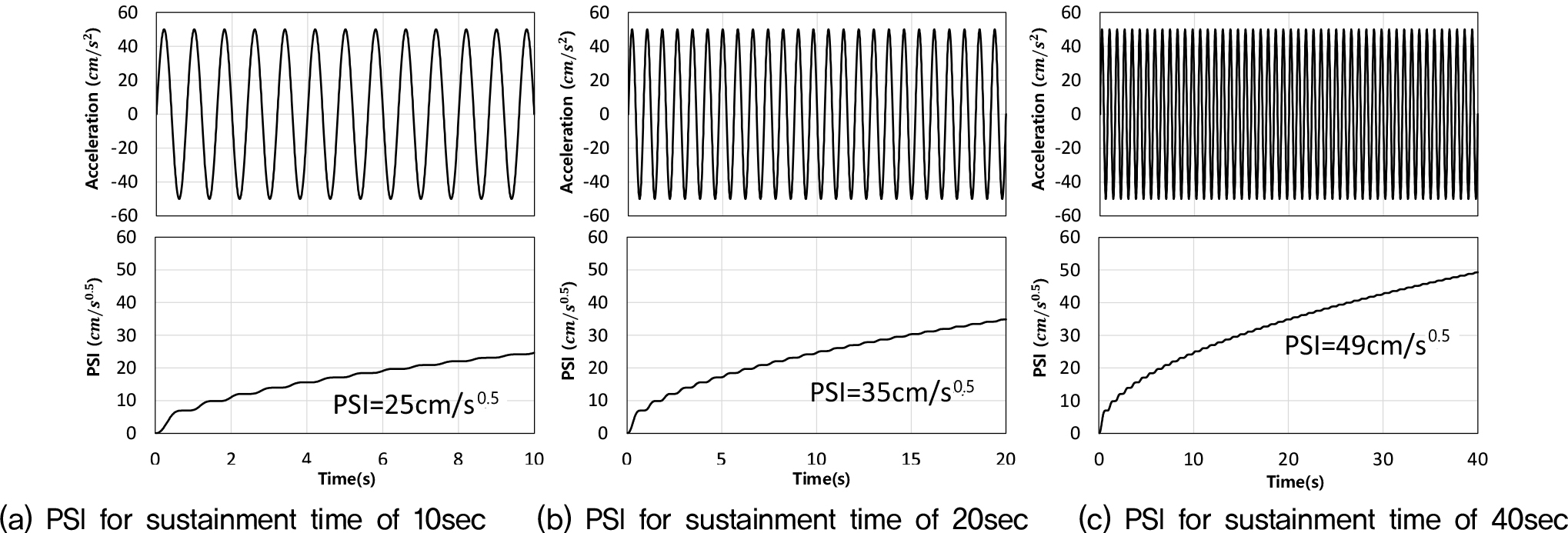
Fig. 6은 50 크기의 동일한 입력 가속도에 대해 지속시간을 10초, 20초, 40초로 증가시켜 속도의 PSI의 변화를 나타낸 것이다. 그림에 나타난 것과 같이 지속시간이 증가함에 따라 속도의 PSI 최대값은 각각 25, 35, 49로 증가함을 알 수 있다.
3.3 입력가속도 크기에 대한 속도의 PSI 거동
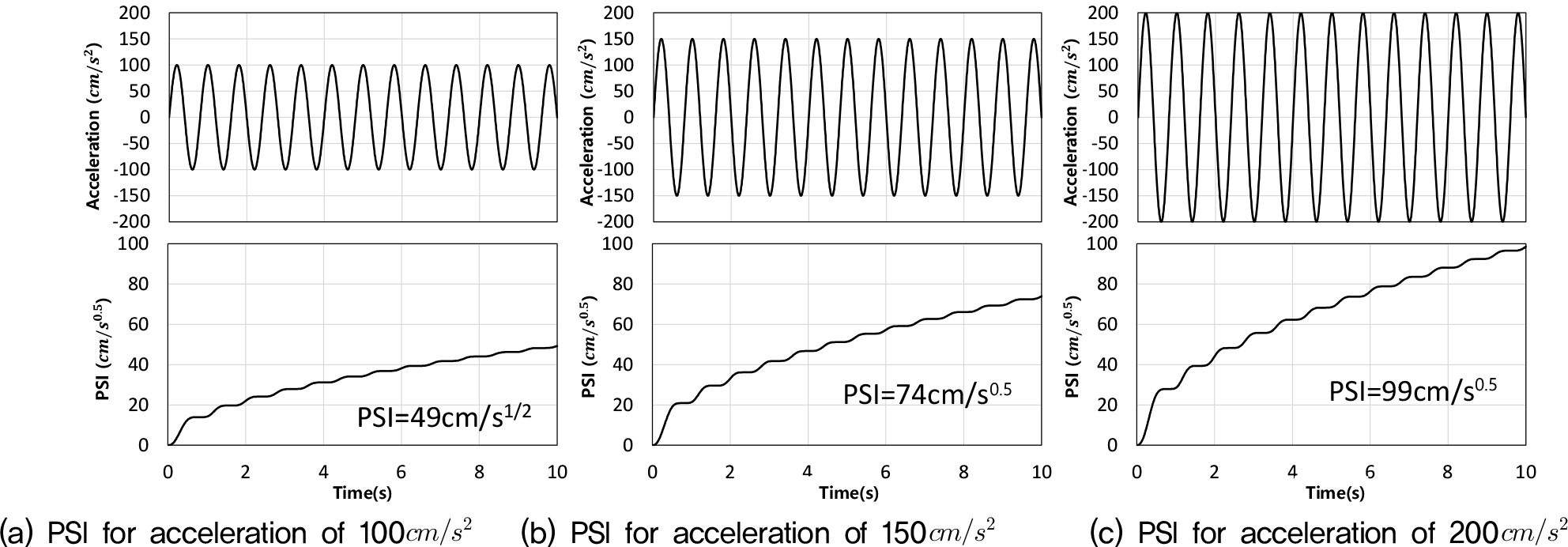
Fig. 7은 입력가속도 크기를 100, 150, 200로 증가시킬 때 속도의 PSI의 변화를 나타낸 것이다. 그림에 나타낸 바와 같이 입력가속도 크기가 증가함에 따라 속도의 PSI 최대값은 각각 49, 74, 99로 증가함을 알 수 있다.
3.4 기존의 간편법(Sone et al., 2012) 산출식
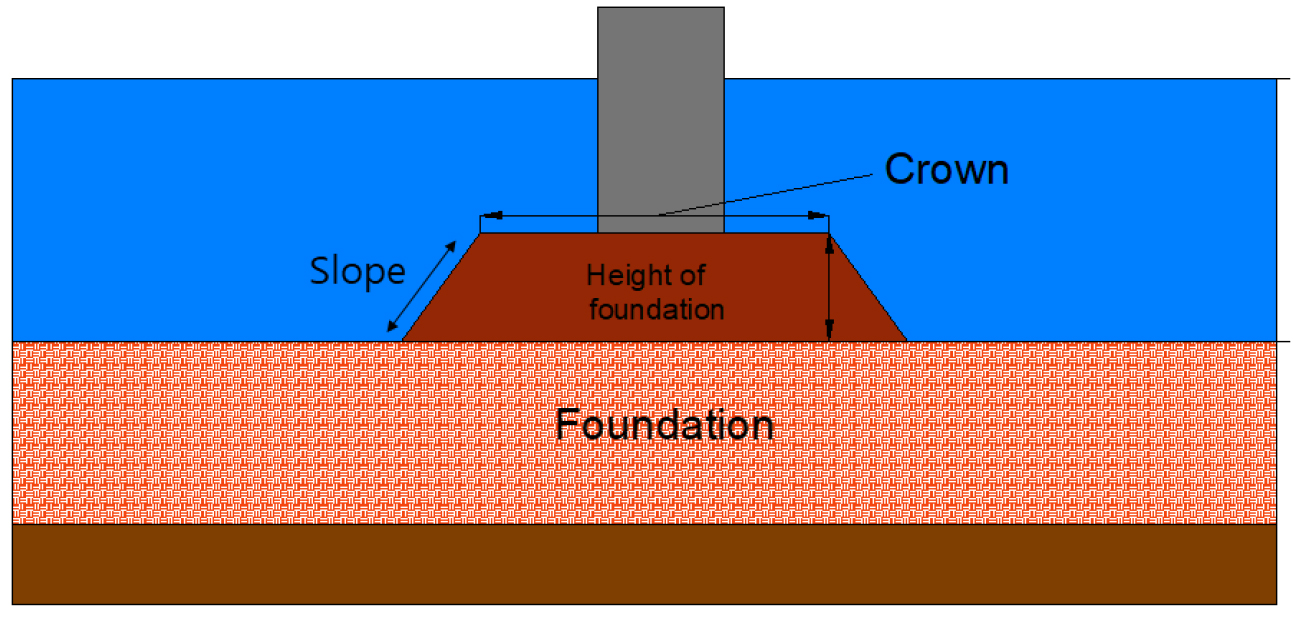
일본의 경우 속도의 PSI 및 구조물의 형상과 제원을 입력하는 것만으로, 지진 시 중력식 방파제에 발생할 침하량을 간단하게 예측할 수 있는 간편법 모델에 관한 연구가 존재한다(Sone et al., 2012). 중력식 방파제란 Fig. 8과 같은 형상의 구조물로, 케이슨식 안벽과는 달리 뒷채움지반이 없다.
1) 기존 속도의 PSI에 의한 침하량 산출식은 다음과 같다.
2) 마운드 천단폭에 관한 보정계수 은 다음 식과 같다.
여기서, y는 보정계수, x는 천단폭(Crown(m))이다.
3) 마운드 높이에 관한 보정계수 는 다음 식과 같다.
여기서, y는 보정계수, x는 마운드 높이(m)이다.
4) 구배에 관한 보정계수 는 다음 식과 같다.
여기서, y는 보정계수, x는 구배이다.
5) 기초지반 두께(Foundation)에 관한 보정계수 는 다음 식과 같다.
여기서, y는 보정계수, x는 속도의 PSI() 이다.
6) 수심에 관한 보정계수 는 다음 식과 같다.
여기서, y는 보정계수이다.
7) 기초지반의 N치에 관한 보정계수 는 다음 식과 같다.
여기서, y는 보정계수, x는 기초지반의 등가N치이다.
8) 속도의 PSI에 관한 보정계수 는 다음식과 같다.
여기서, y는 보정계수, x는 속도의 PSI() 이다.
9) 방파제 중량에 관한 보정계수 는 다음 식과 같다.
여기서, y는 보정계수, x는 단위면적당 방파제중량()이다. 속도의 PSI값이 45~90()의 사이일 때는 각각의 보정계수를 선형보간한 값을 사용한다.
10) 제방과 사석의 차이에 관한 보정계수 는 다음 식과 같다(Sone et al., 2012).
여기서, y는 보정계수이다.
11) 기준침하량에 관한 보정계수 은 다음 식과 같다(Atsushi, 2015).
4. 수치해석을 이용한 케이슨식 안벽의 내진안정성 평가
4.1 수치해석 개요
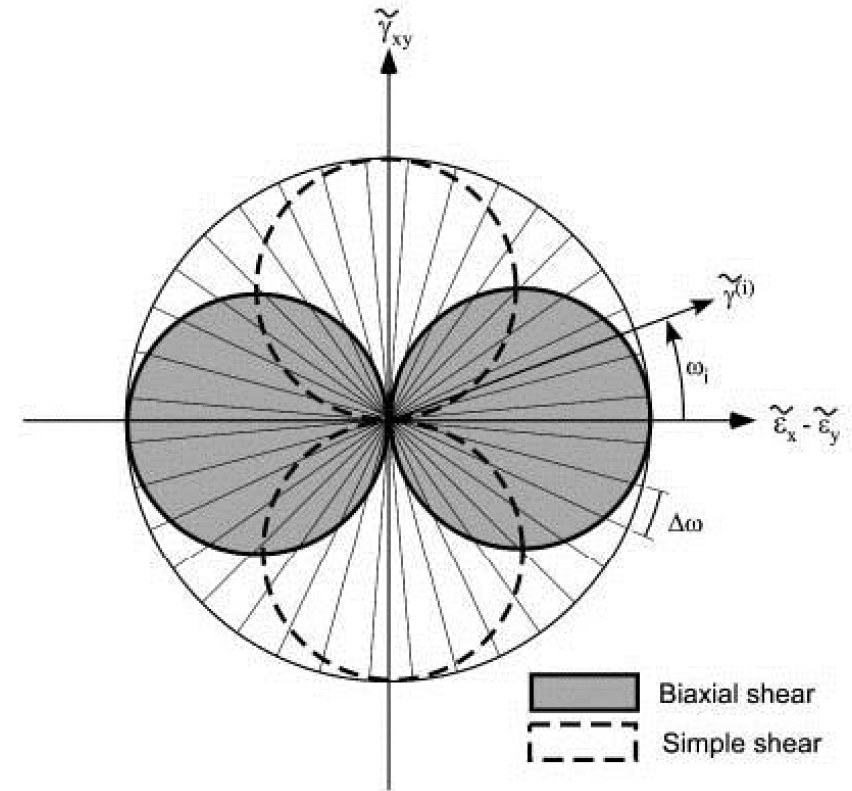
본 연구는 FLIP Consortium에서 개발한 지반수치해석 프로그램인 FLIP(Finite element analysisi program of Liquefaction Process)을 이용하였다. FLIP은 유한요소법 기반의 지반 진동에 의한 지반-구조물 동적상호작용 거동 해석 프로그램으로 Lee et al.(2018), Kim(2019), Kim et al.(2019)등 많은 연구에 사용되고 있으며, 주로 지반 진동에 의한 액상화 현상의 피해와 해안구조물의 피해 예측에 이용되고 있다. 흙에 대한 유효응력모델은 다중전단메커니즘모델을 이용하며, 이 모델의 원형고정경계는 Fig. 9와 같이 전단변형영역과 무한개의 가상스프링 경계의 연결로 정의되는 이동절점으로 나타내며 각 스프링은 다양한 방향을 가지는 실제 다중전단메커니즘이라 할 수 있고 이를 통해 흙의 탄소성 거동을 모사한다(Iai et al., 1992a, 1992b).
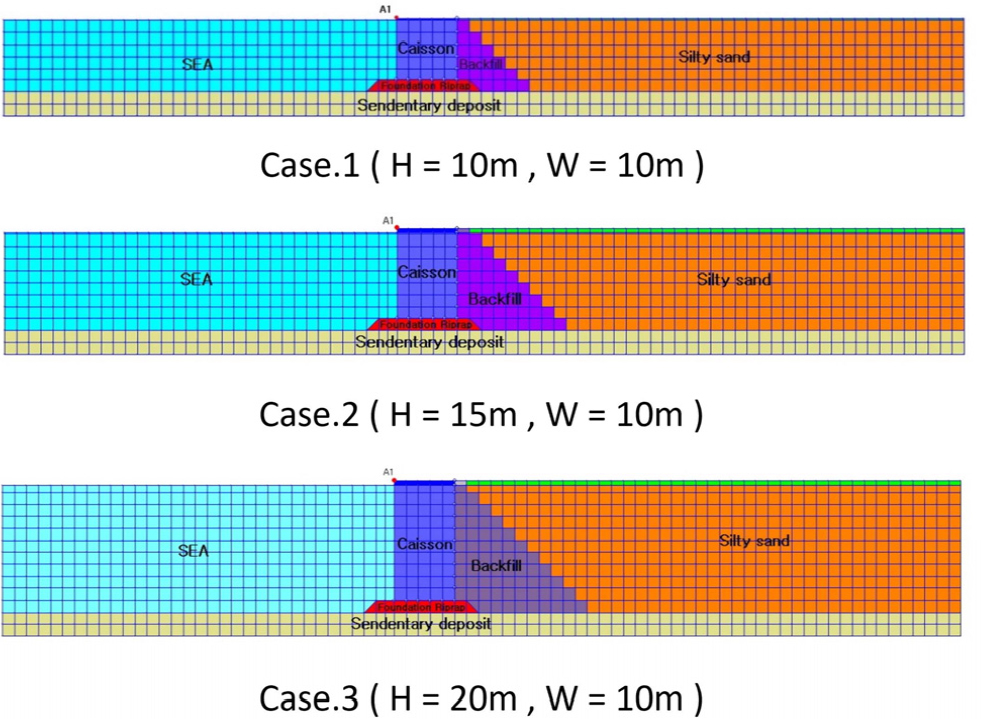
4.2 수치해석 모델
본 연구에서 적용한 수치해석 단면은 인천항 국제여객부두 케이슨식 안벽 단면을 토대로 구성하였으며, 아래 Fig. 10과 같이 케이슨 폭(W)/케이슨 높이(H)에 따라 3가지 케이스로 구분하여 수치해석을 진행하였다. 3가지 케이스 전부 케이슨의 높이를 제외한 모든 조건이 동일하다. Silty sand, Backfill, Foundation Riprap, Sedentary deposit 등 흙 요소에는 Multi-spring model을 적용하였다. Caisson은 linear Plane 모델로 해석하였다. 그리고 바다(SEA)는 fluid 모델로 해석하였다. 그림에 표시된 A1은 케이슨 천단부에 위치하며, 지진 시 케이슨의 변위를 출력하는 절점이다. 수치해석 단면의 양단은 자유지반경계해석을 통해 무한으로 확장시켜 안정성을 검토할 수 있도록 하였다. 경계조건은 경계면에서의 응력집중이나 반사파의 영향을 최소화하기 위해 점소성으로 설정하였다. 본 연구에 적용된 입력 지진가속도는 Sin파로, Fig. 11와 같다. 실제 지진파의 경우 진폭과 지속시간 외에 파악하기 어려운 외부 특성이 포함되어 있다. 하지만 Sin파의 경우 순수하게 진폭과 지속시간만을 고려할 수 있기 때문에 본 연구에서는 주파수 1.25Hz, Sin파; 0.8‘초(sec)“를 이용하였다. 최근 발생한 경주 지진과 포항 지진의 경우 지진의 지속시간이 10초 이내이며 속도의 PSI는 10 이하였다. 따라서 이를 포함하는 범위로 입력파의 지속시간은 10초, 입력가속도의 크기는 200Gal이내로 설정하여 수치해석을 진행하였다.
4.3 액상화 입력변수 산정
본 연구에서는 2012년 인천항 정밀점검 및 정밀안전진단보고서를 참조하여 Table 2와 같이 지반정수를 적용하였다. Table 3, Fig. 9의 액상화 프론트와 관련하여 과잉간극수압의 증가에 의한 유효응력의 소실을 모사하는 액상화 관련 입력변수(Iai et al., 1992b)를 나타내고 있으며, Silty sand의 경우 N치를 10, 15, 20, 25로 가정하여 각각 수치해석을 진행하였다. 또한, Sedentary deposit 지반의 N치는 20으로 가정하였다. Shear Lock problem(WG, 2009)의 간편법을 통해 N치, 유효상재압, 세립분율 N치에 따른 뒷채움지반의 액상화 입력변수를 산정하였다.
Table 2.
Soil parameters on Incheon port report
5. 해석결과
5.1 간편법과 수치해석 결과 비교 – 수평변위
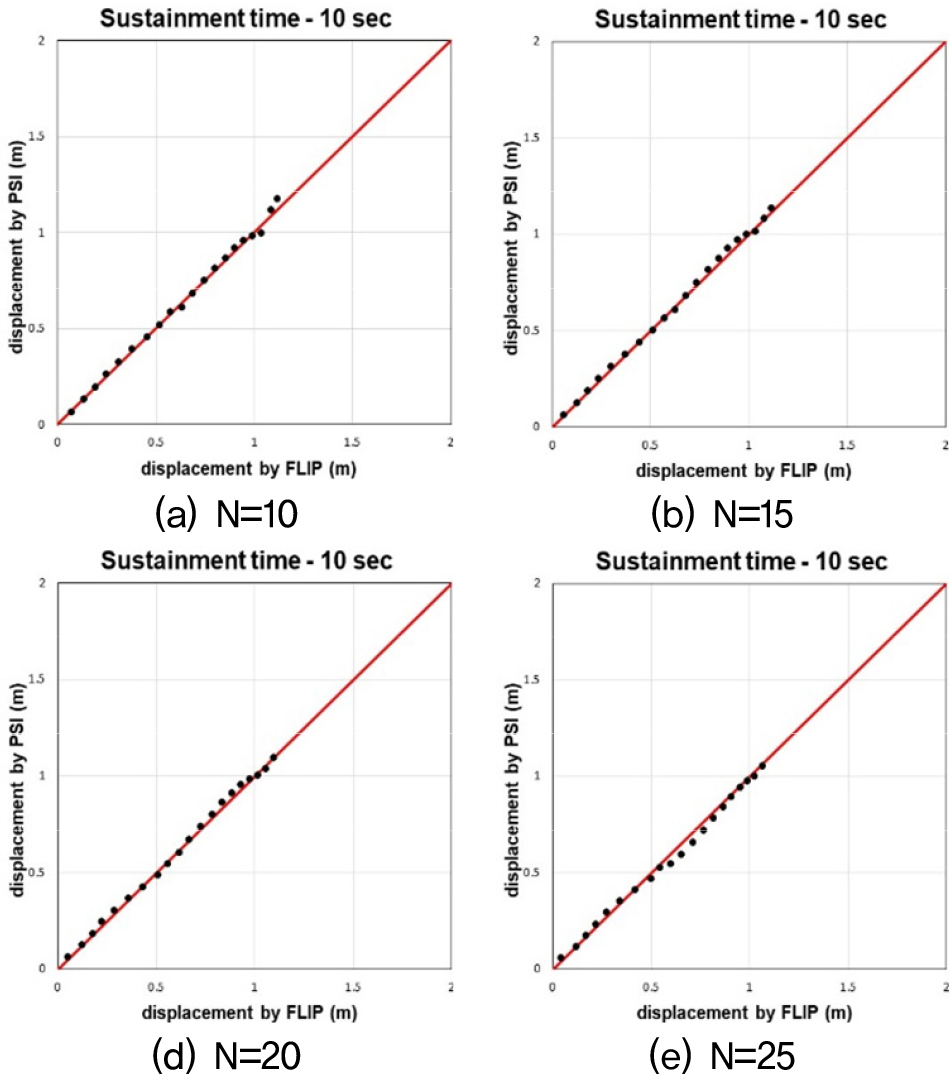
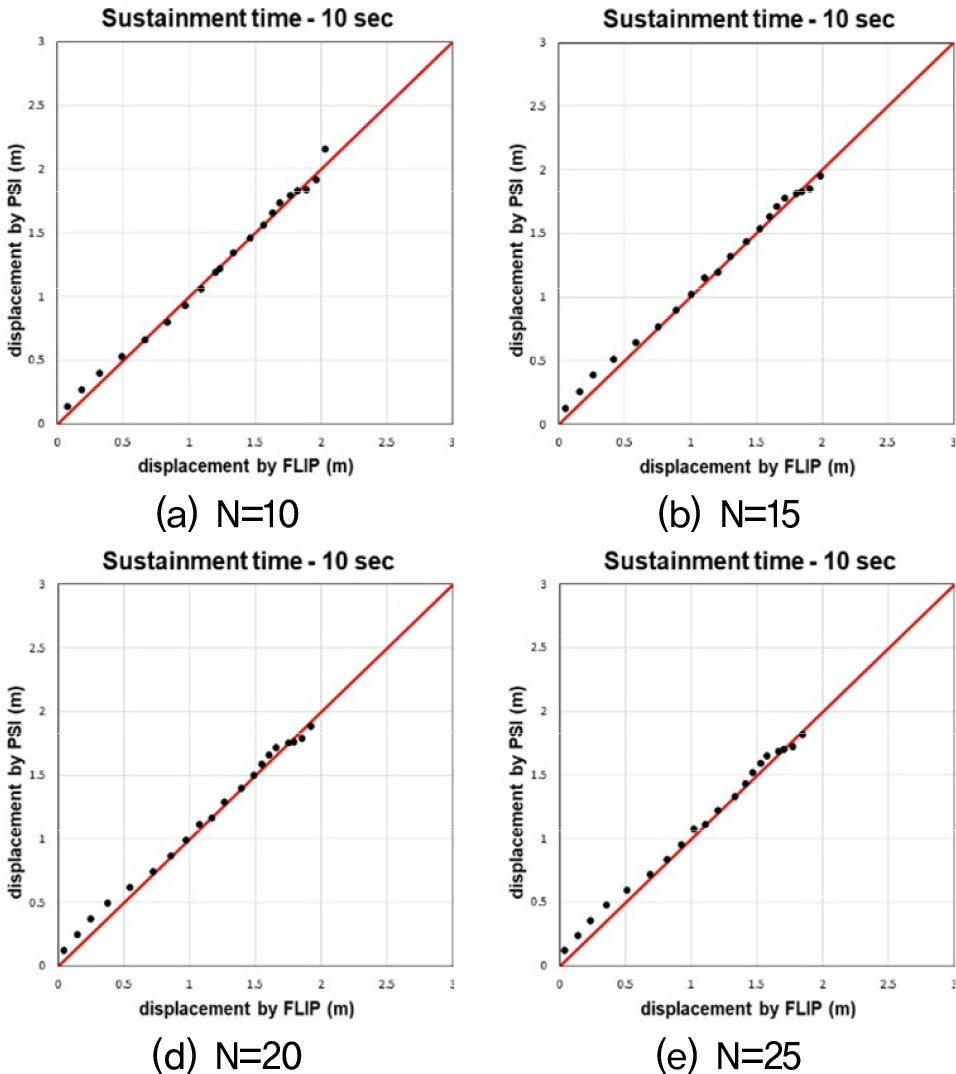
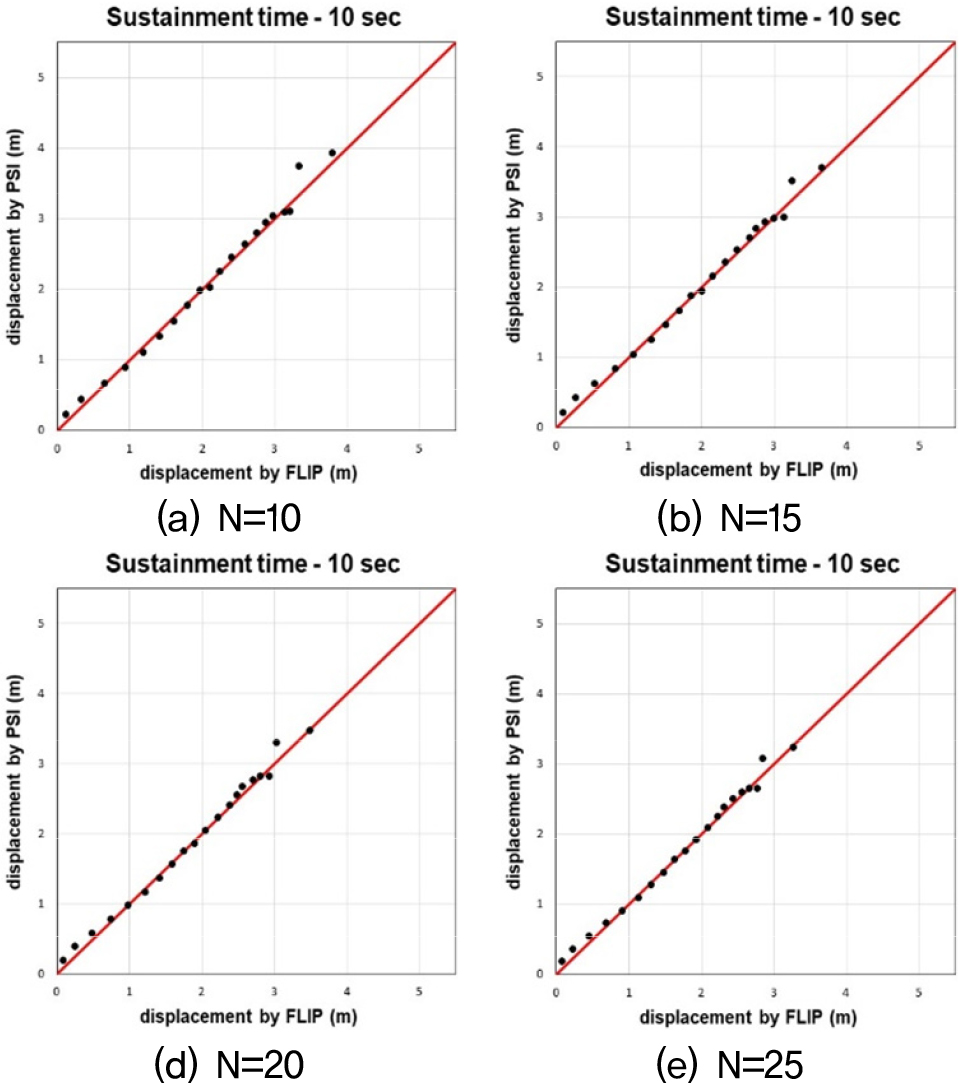
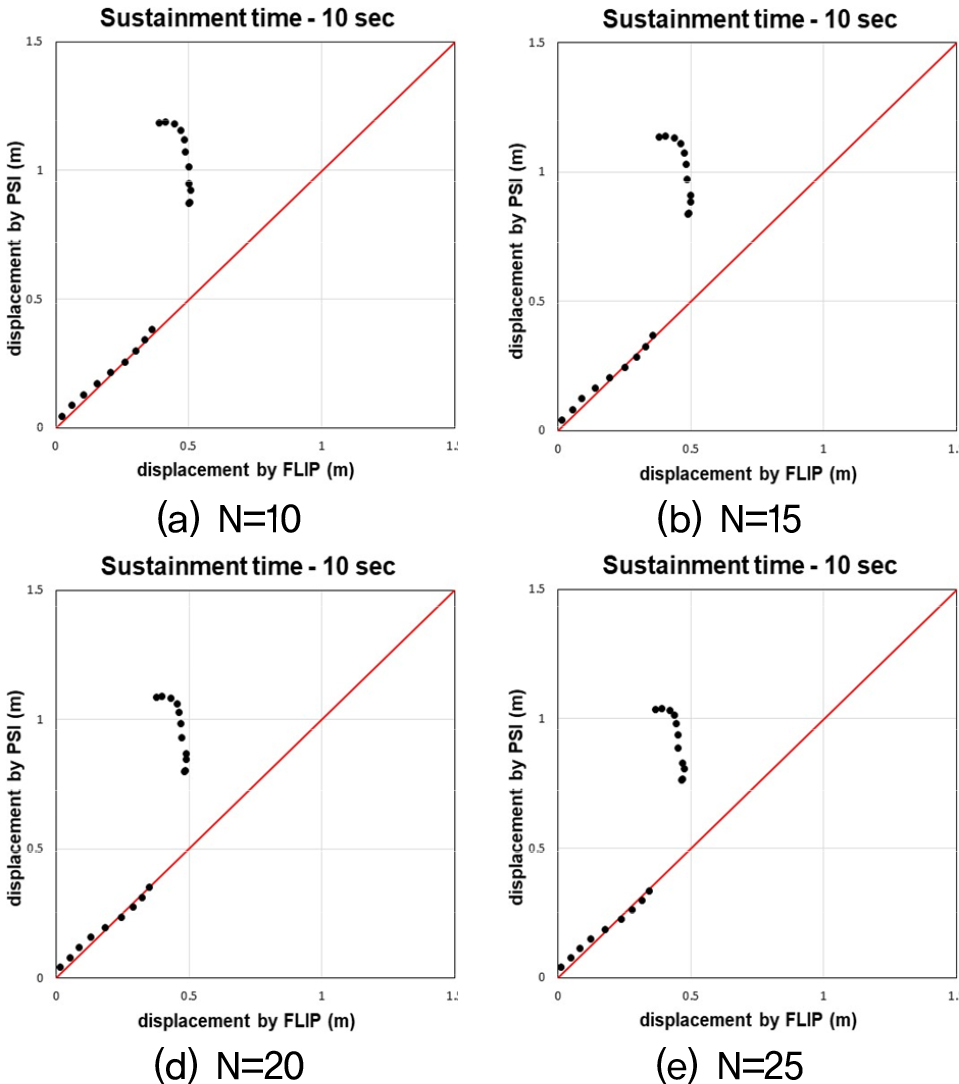
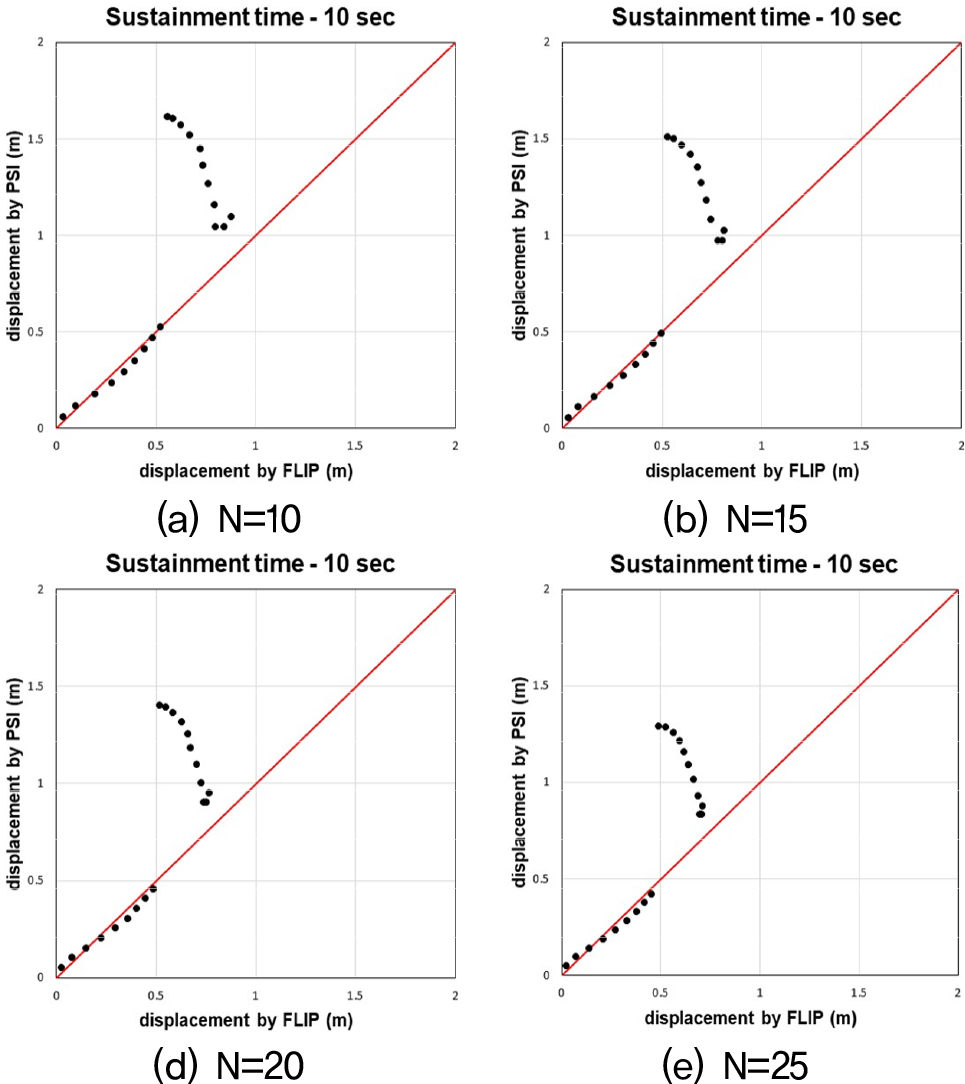
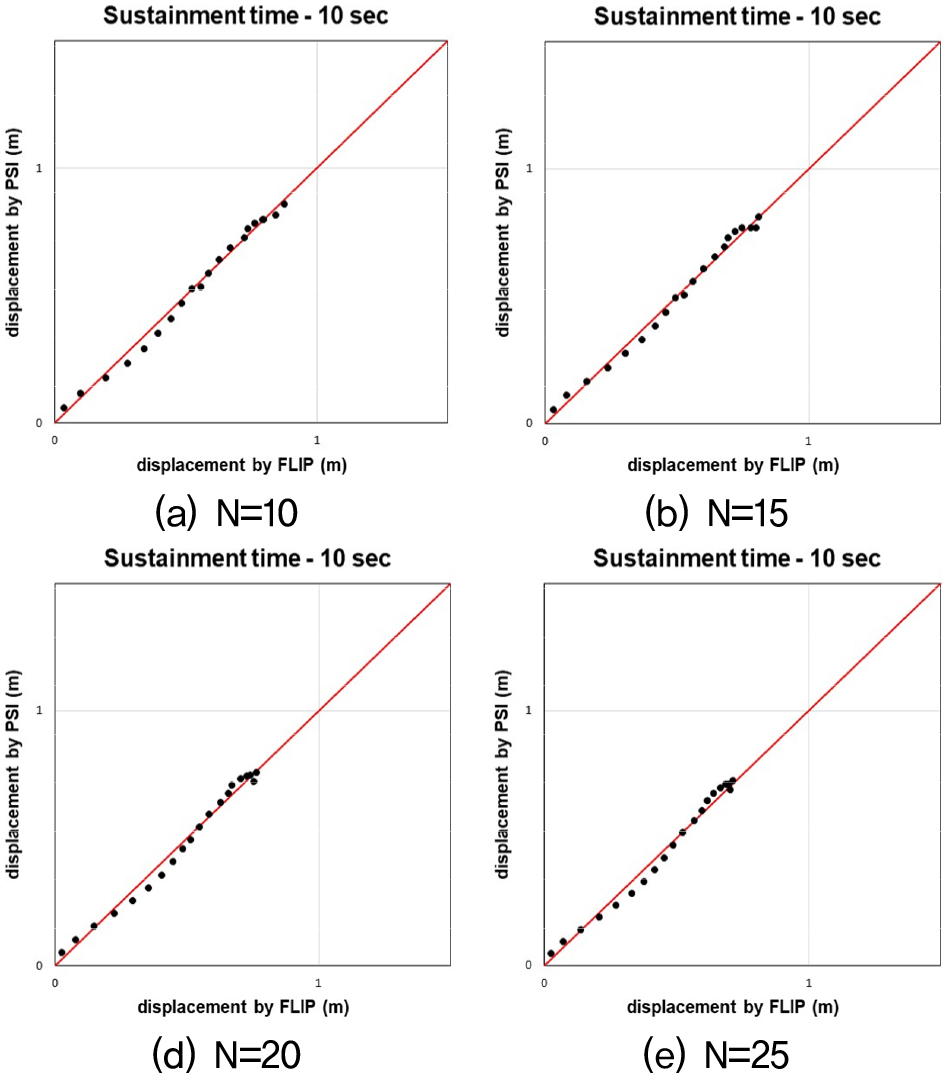
Fig. 12, 13, 14는 수치해석과 간편법으로 산출된 수평변위 값을 비교한 그래프다. 비교결과, 기존의 간편법(Sone et al., 2012)을 케이슨식 안벽의 수평변위를 예측하는데 적용하기엔 한계가 있음을 확인하였다. 기존의 간편법은 지진 시 방파제의 침하량을 예측하기 위한 간편법 모델이기 때문에 안벽구조물 뒷채움지반의 N치를 고려하지 못한다. 이러한 차이로 인해 뒷채움지반의 N치가 증가함에 따라 수치해석과 간편법 사이의 오차가 커지는 경향이 나타난다. 따라서 케이슨식 안벽의 수평변위 산정 시 뒷채움지반 N치에 따른 추가적인 보정계수가 필요하다고 판단하여, 이에 관한 연구를 진행하였다. 또한, 속도의 PSI가 45 이상인 범위에서 간편법으로 산출된 수평변위 값이 속도의 PSI가 45 미만인 경우에 비해 급증하거나, 속도의 PSI는 증가하지만 수평변위량은 오히려 감소하는 양상을 띄기도 한다. 이러한 양상을 띄는 이유는, 속도의 PSI가 45 이상일 때 속도의 PSI에 관한 보정계수인 보다 다른 보정계수들에 의해 더 큰 영향을 받기 때문이다. 이를 보완하기 위해 기존 속도의 PSI에 관한 보정계수 을 수정할 필요가 있다고 판단하였고, 이에 관한 연구를 진행하였다. 마지막으로, 간편법 모델을 다양한 단면과 형상의 안벽에도 적용할 수 있도록 W/H비 범위에 관한 보정계수가 필요하다고 판단하여, 이에 관한 연구를 진행하였다.
5.2 보정계수 제안 – 수평변위
앞선 결과분석을 통해, 기존 속도의 PSI에 관한 보정계수인 을 수정할 필요가 있음을 확인하였다. 이에 따라 회귀분석을 통해 을 수정한 보정계수 을 아래 식 (13)과 같이 제안한다.
여기서, x는 속도의 PSI이다.
또한, 기존의 간편법이 케이슨식 안벽의 뒷채움 지반을 고려하지 못해 생기는 오차를 보정해주기 위해, 뒷채움지반 N치에 관한 보정계수 을 아래 식 (14)와 같이 제안한다.
여기서, x는 뒷채움지반의 N치이다.
마지막으로, 간편법을 다양한 형상 및 단면에도 적용할 수 있도록 W/H비 범위에 관한 보정계수의 필요성에 대해 앞서 확인하였다. 따라서 회귀분석을 통해 W/H 비 범위에 따른 보정계수 을 아래 식 (15)와 같이 제안한다.
여기서, X는 W/H이다.
5.3 보정계수 적용 후 간편볍과 수치해석 결과 비교 – 수평변위
새로운 보정계수()를 적용한 간편식은 아래 식(16)과 같고, 지진 시 케이슨식 안벽의 수평변위를 예측할 수 있는 최종 산출식이다.
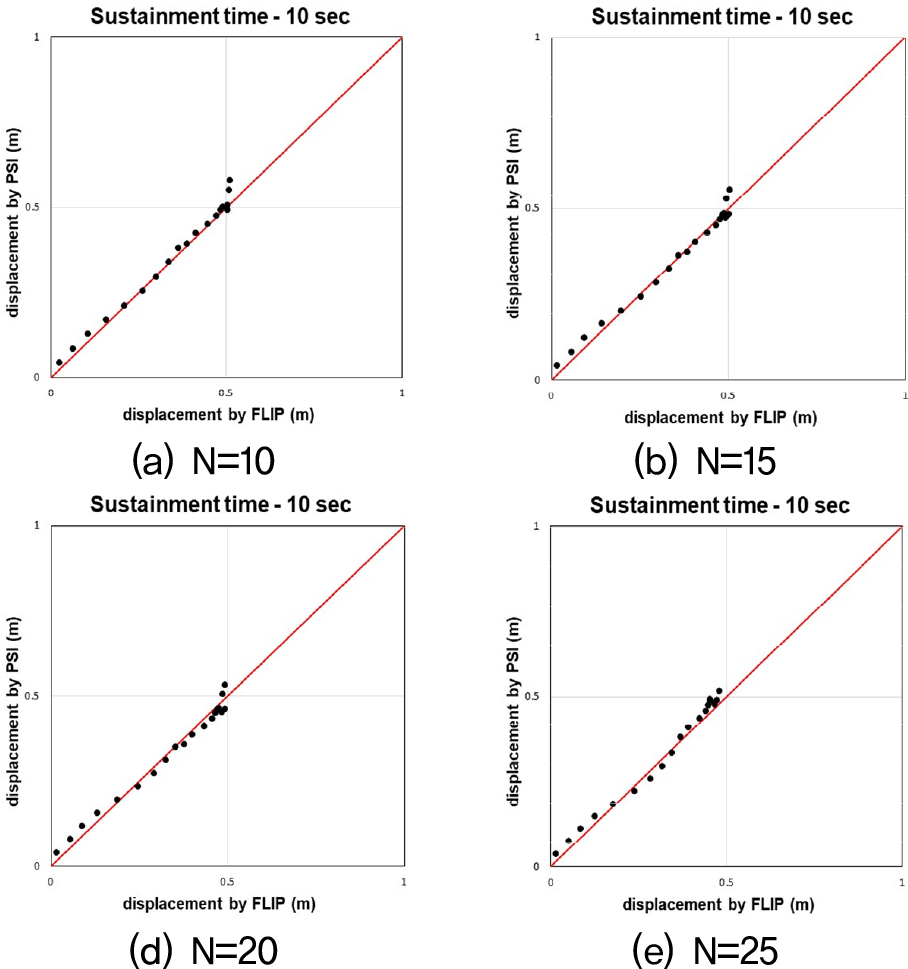
아래의 Fig 15, 16, 17은 수치해석으로 산출된 값과 위의 식(16)으로 산출한 값을 비교 분석한 그림이다. 보정계수 적용 후, 속도의 PSI가 45 이상일 때 크게 발생했던 오차가 확연하게 줄어 간편법으로 예측한 값과 수치해석 값이 거의 일치함을 확인할 수 있다.
5.4 간편법과 수치해석 결과 비교 – 침하량
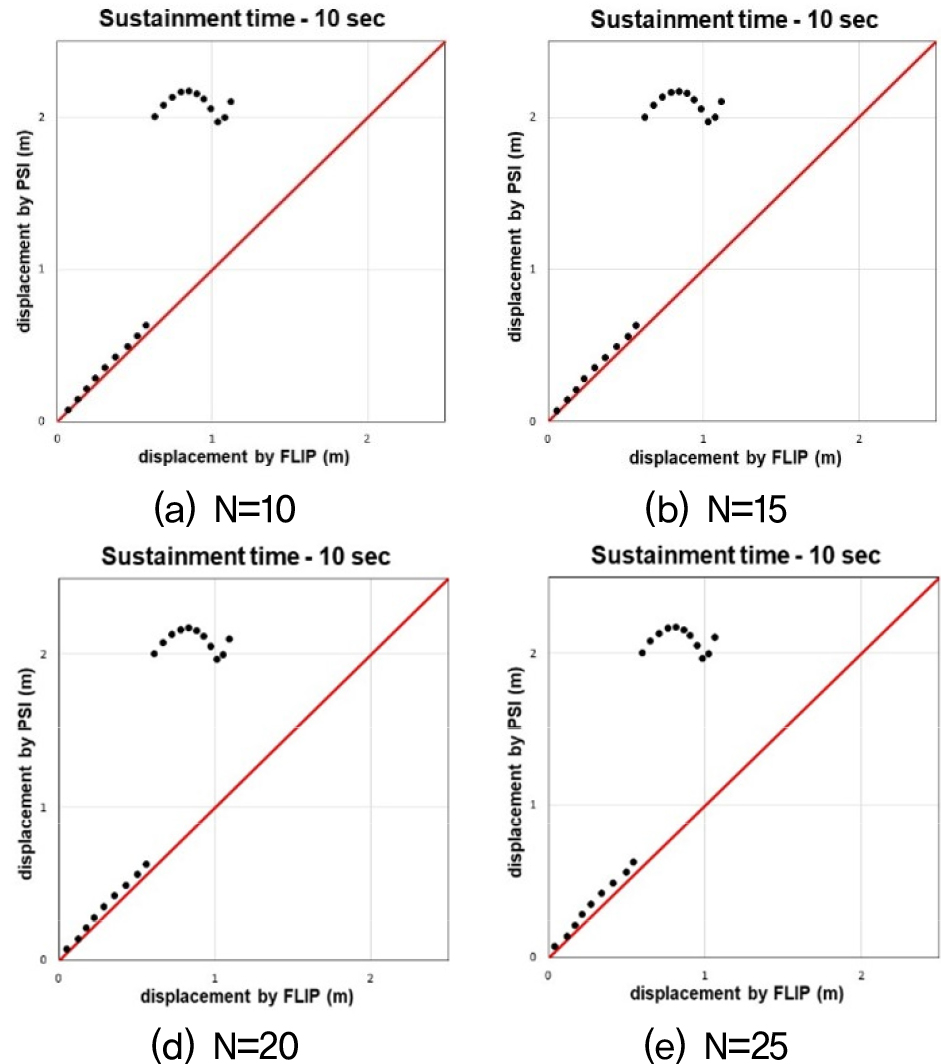
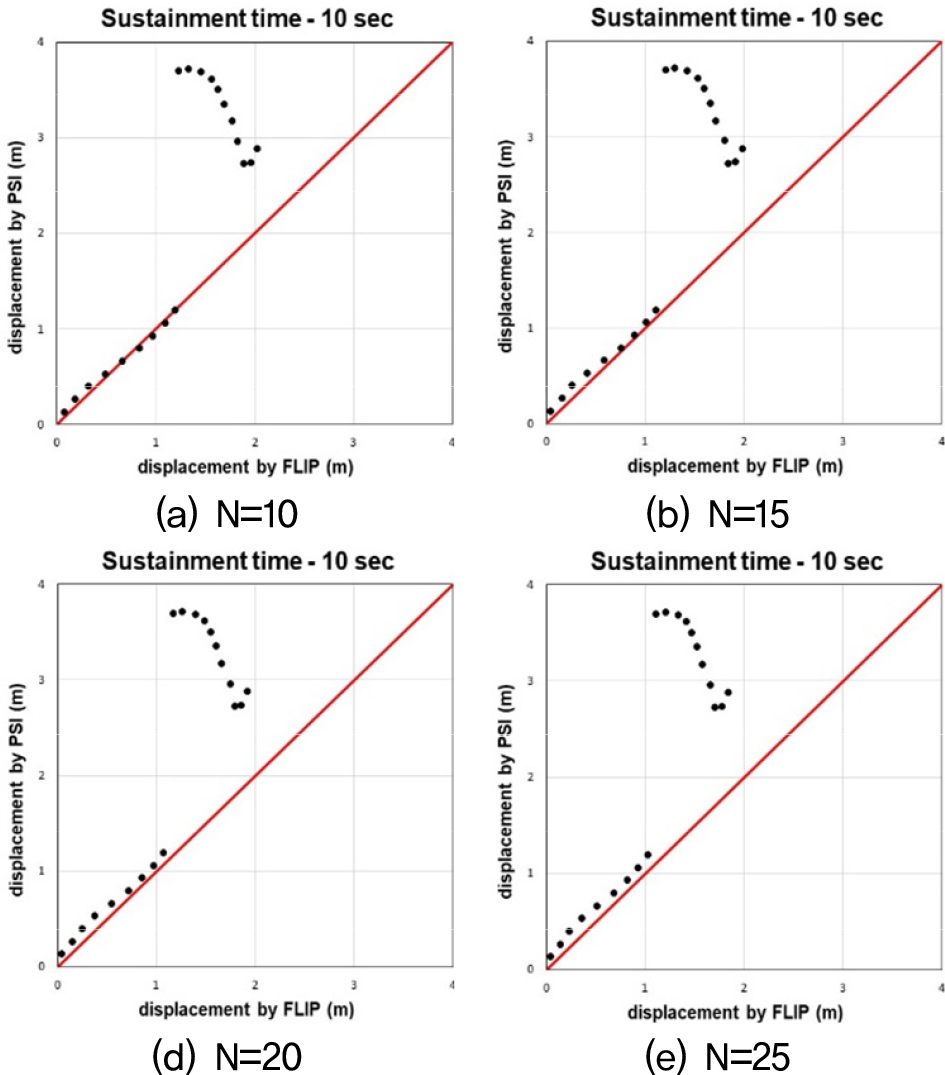
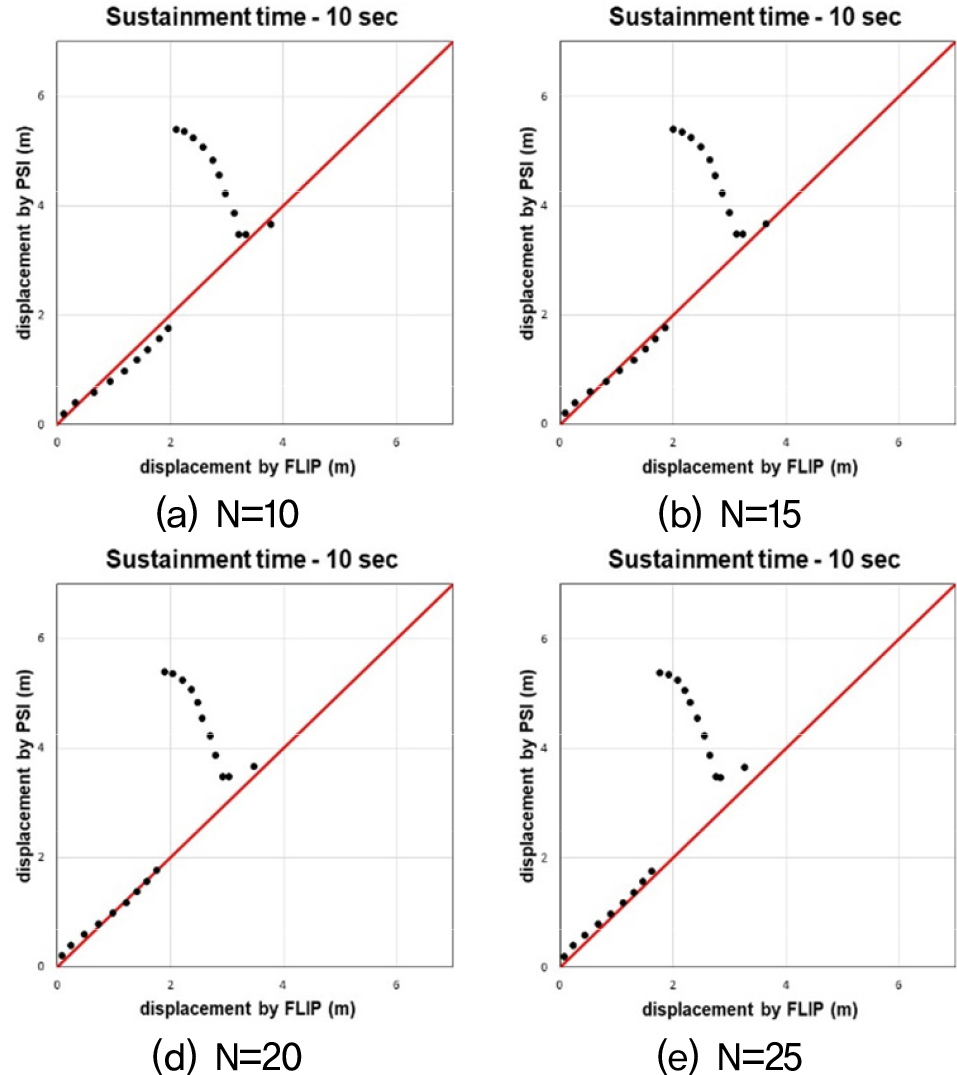
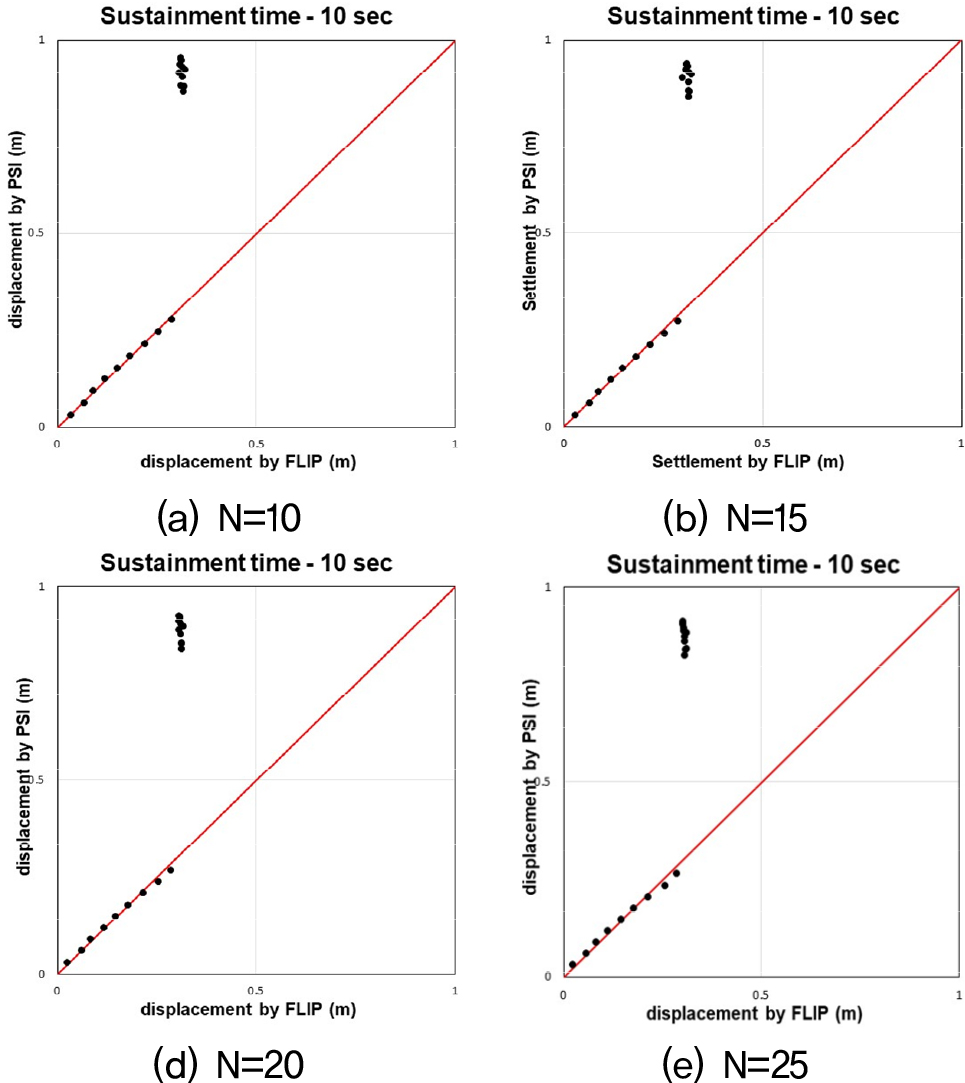
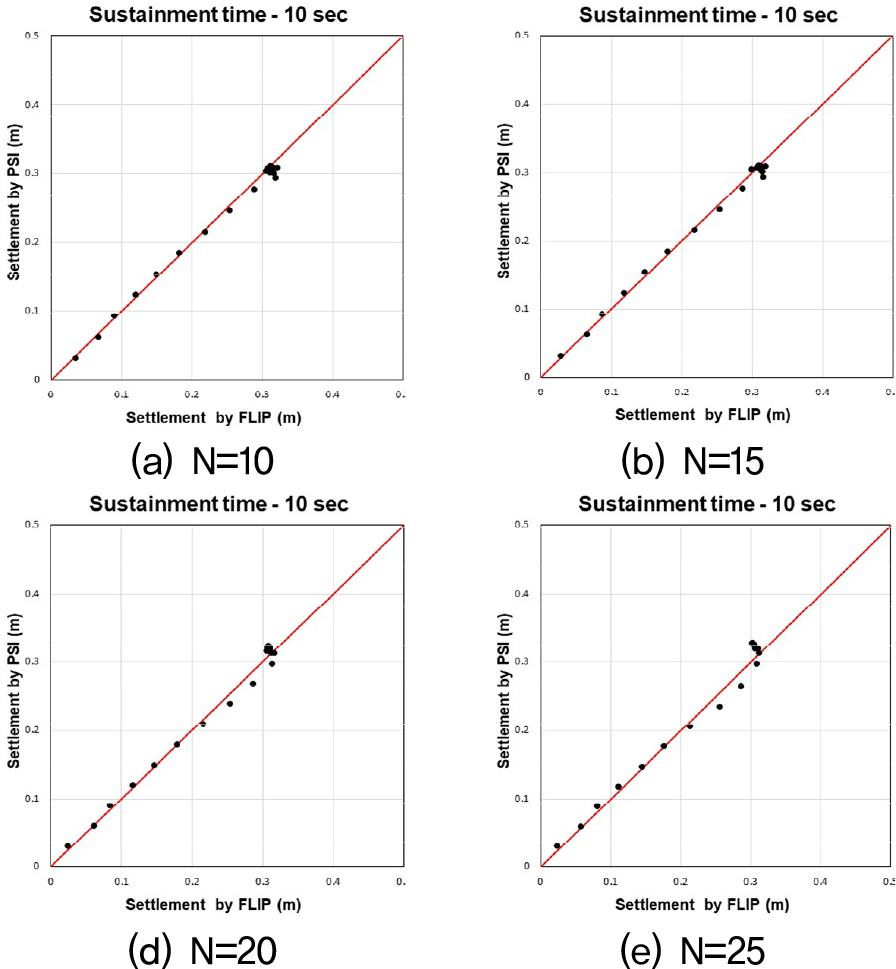
Fig. 18, 19, 20은 수치해석과 간편법으로 산출된 침하량 값을 비교한 그래프다. 비교결과, 수평변위의 경우와 마찬가지로 기존의 간편법(Sone et al., 2012)을 케이슨식 안벽의 침하량를 예측하는데 적용하기에 한계가 있음을 확인하였다. 또한, 수평변위의 경우와 거의 동일한 양상으로 오차가 발생하는 것을 확인하였다. 따라서 이를 보정하기 위해 기존의 간편법의 보정계수 중 하나인 속도의 PSI에 관한 보정계수를 수정하고, 뒷채움지반 N치에 관한 보정계수 및 W/H비 범위에 따른 보정계수를 추가하였다.
5.5 보정계수 제안 – 침하량
우선 기존 속도의 PSI에 관한 보정계수 을 수정한 을 아래 식 (17)와 같이 제안한다.
여기서, x는 속도의 PSI이다.
그리고, 케이슨식 안벽 뒷채움지반 N치에 관한 보정계수 을 아래 식 (18)와 같이 제안한다.
여기서, x는 뒷채움지반의 N치이다.
마지막으로 W/H비 범위에 따른 보정계수 을 아래 식 (19)와 같이 제안한다.
여기서, X는 W/H이다.
5.6 보정계수 적용 후 간편법과 수치해석 결과 비교 – 침하량
새로운 보정계수()를 적용한 간편식은 아래 식(20)와 같고, 지진 시 케이슨식 안벽의 침하량을 예측할 수 있는 최종 산출식이다.
아래의 Fig. 21, 22, 23은 수치해석으로 산출된 값과 위의 식 (20)으로 산출한 값을 비교분석한 그림이다. 보정계수 적용 후, 속도의 PSI가 45 이상일 때 크게 발생했던 오차가 확연하게 줄어 간편법으로 예측한 값과 수치해석 값이 거의 일치함을 확인할 수 있다.
6. 활용방안 및 결론
6.1 활용방안
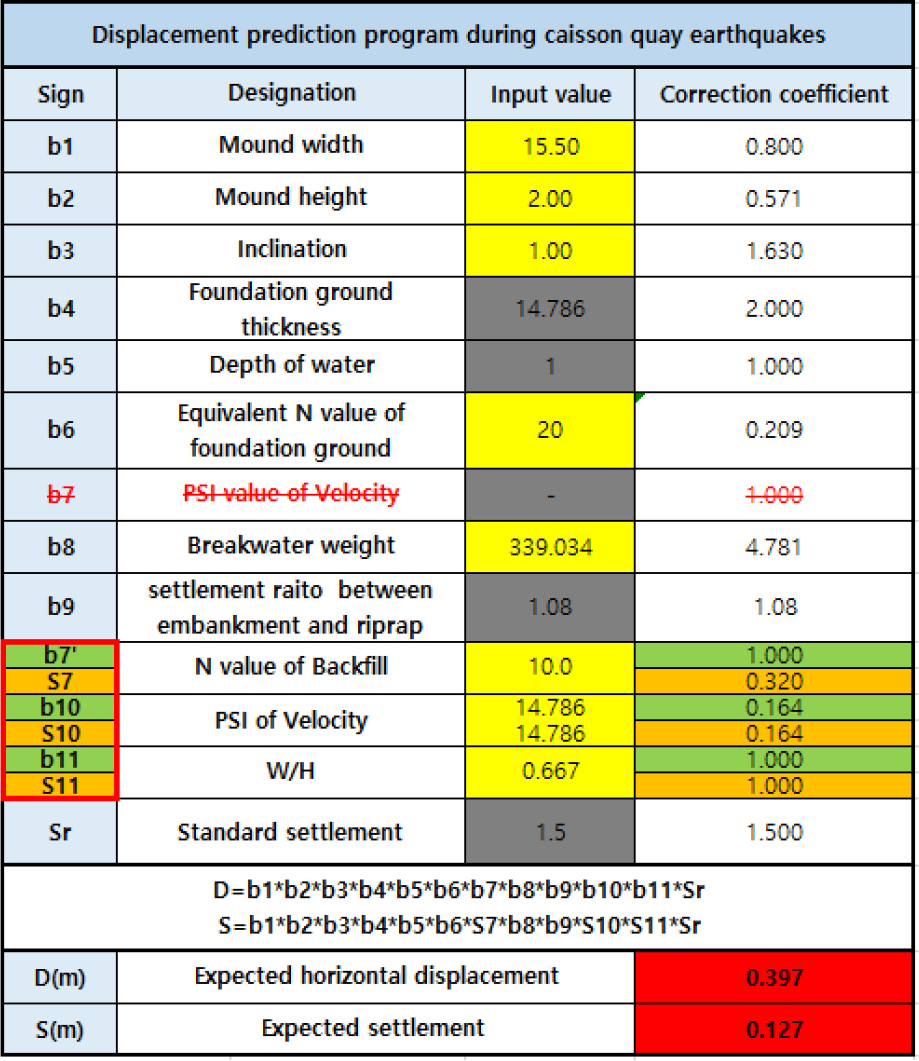
본 연구에서 제안한 간편법을 토대로 Fig. 24와 같이 엑셀을 활용한 차트식 내진안정성 평가시스템을 개발하여, 실무자가 빠르고 쉽게 케이슨식 안벽의 피해를 예측할 수 있도록 활용할 수 있을 것으로 기대된다.
6.2 결론
본 연구는 속도의 PSI의 특성과 중력식 방파제의 침하량을 예측하기 위해 개발된 Sone et al.(2012)의 간편법을 활용하여, 지진 시 케이슨식 안벽구조물의 변위량을 예측하기 위한 간편법 개발을 목적으로 진행되었다. 단면의 형상 및 제원, 그리고 입력지진파를 통해 구한 속도의 PSI를 기존의 간편법 모델(Sone et al., 2012)에 대입하여 수치해석 값과 비교분석 하였다. 비교분석을 통해 추가적인 보정계수를 제안하여 간편법의 오차를 보정하였다. 결론은 다음과 같다.
(1)지진시 방파제의 침하량에 예측하기 위해 개발한 기존의 간편법(Sone et al., 2012)으로 지진 시 발생할 케이슨식 안벽구조물의 변위량을 예측하는 것에는 한계가 있다는 걸 확인하였다. 기존의 간편법은 케이슨식 안벽의 뒷채움지반을 고려할 수 없기 때문이다. 그로 인해 발생하는 오차와 속도의 PSI가 45이상 범위에서 급증하는 오차를 보정해주기 위해, 케이슨식 안벽구조물의 뒷채움지반 N치에 관한 보정계수 및 W/H비 범위에 관한 보정계수, 그리고 기존 속도의 PSI를 수정한 보정계수를 제안하였다.
(2)새로운 보정계수를 추가한 간편법과 수치해석을 비교분석한 결과, 둘의 값이 거의 일치함을 확인하였다.
(3)이 간편법을 활용하여 지진 시 위험도가 큰 케이슨식 안벽구조물들을 빠르게 예측할 수 있을 것으로 사료된다. 단, 본 연구에서의 간편법은 인천항에 한정해서만 사용 가능하다. 지반조건이 다른 항에 대한 연구를 지속적으로 진행하여, 모든 국내 항에 간편법을 적용할 수 있도록 추가적인 연구가 필요할 것으로 판단된다.