1. 서 론
2. 데이터 수집 및 상관성 검토
2.1 데이터 수집
2.2 점토의 물리적 특성별 회귀분석
3. 기계학습 알고리즘 및 회귀모델 결과
3.1 오렌지 마이닝
3.2 기계학습 알고리즘
3.3 회귀 모델 결과
4. 회귀모델 평가기준
5. 결 론
1. 서 론
연약 지반을 개량하고 그 상부에 구조물을 시공하면서 지반 침하량에 대한 연구는 현재까지 계속 이어지고 있다. 연약한 점토지반에 구조물을 건설한 경우 과도한 침하가 발생하여 구조물의 안정성에 문제가 발생하는 일이 빈번하게 발생하고 있다(Lim, 2019; Kim, 2021). 이를 방지하기 위해서는 정확한 침하량을 예측한 것이 중요하다. 침하량을 산정하기 위하여 Terzaghi 1차 압밀이론을 주로 활용하고 있는데 여기서, 압축지수를 압밀시험으로 산정하거나 다른 흙의 물리적 특성을 통해 예측하는 것은 매우 중요한 일이다. 이에 따라 국·내외적으로 압축지수를 예측하는 많은 연구가 수행되었다.
Barron(1948), Mikasa(1963), Gibson et al.(1967)은 침하량을 예측하기 위하여 다양한 압밀침하 이론을 발표하였다. Nishida(1956)는 간극비(eo), Terzaghi and Peck(1967)Mayne(1980)는 액성한계(LL), Azzouz et al.(1976)은 앞서 언급한 물리적 특성 모두 적용할 수 있는 관계식을 제시하였다. Yoon and Kim(2003)은 자연함수비, 초기 간극비, 비중, 액성한계, 소성지수, 압축지수 값을 Linear Regression 하여 압축지수에 대한 회귀식을 도출하였다. Lee et al.(2022)은 부산, 광양, 목포지역을 대상으로 점토의 자연함수비, 액성한계, 소성지수, 초기 간극비, 압축지수 데이터를 수집하여 기계학습 알고리즘인 Random Forest, Linear Regression, Ridge, Lasso, SVM, XGBoost, LightGBM, DNN에 적용하여 압축지수 예측 모델을 제시하는 연구를 시행하여 압축지수 예측 식을 도출하였다. 최근에 Kang et al.(2024)는 부산항 신항 및 북항, 낙동강 중·하류, 김해, 양산 및 울산 지역의 점토를 채취하여 물성 시험 및 표준 압밀시험을 실시한 후, 결과를 활용하여 함수비를 기준으로 압축지수, 처녀 압축지수, 압밀계수, 팽창지수, 2차 압축지수 등을 Linear Regression을 실시하고, 그에 따른 압축지수, 처녀 압축지수, 압밀계수, 팽창지수, 2차 압축지수에 대한 회귀식을 도출하였다.
본 연구에는 Kang et al.(2024) 연구의 연장으로 부산항 신항 점토를 대상으로 압축지수 예측연구를 수행하였다. 이를 위하여 부산항 신항 점토에 대한 함수비, 간극비, 액성한계, 소성한계, 압축지수의 데이터를 수집하여 데이터셋을 구축하고 기계학습 알고리즘인 Random Forest, Neural Network, Linear Regression, AdaBoost, Gradient Boosting에 적용하여 그 결과를 비교하여 최적의 예측 모델을 선정하였다. 사용한 기계학습 프로그램은 오픈소스인 오렌지 마이닝을 이용하였다.
2. 데이터 수집 및 상관성 검토
2.1 데이터 수집
본 연구는 Kang et al.(2024) 부산항 신항의 점토 시료를 채취하여 직접 물성 시험 및 표준압밀시험을 실시하여 나온 실험 결과를 활용하여 데이터 셋을 구축하였다. 구체적으로 값의 범위를 보면 함수비 26.39~87.79, 간극비 0.714~2.383, 액성한계 34.35~78.20, 소성한계 17.10~33.10, 압축지수 0.159~1.190 등이다. Table 1은 부산항 신항의 점토 시료를 물성 시험 및 표준압밀시험을 실시하여 결과를 정리한 것이다.
Table 1.
Regional data range and mean value
| Water Content | Void Ratio | Liquid Limit | Plastic Limit | Compression Index |
| 26.39~87.79 | 0.714~2.383 | 34.35~78.20 | 17.10~33.10 | 0.159~1.190 |
| 57.09 | 1.549 | 56.28 | 25.1 | 0.675 |
2.2 점토의 물리적 특성별 회귀분석
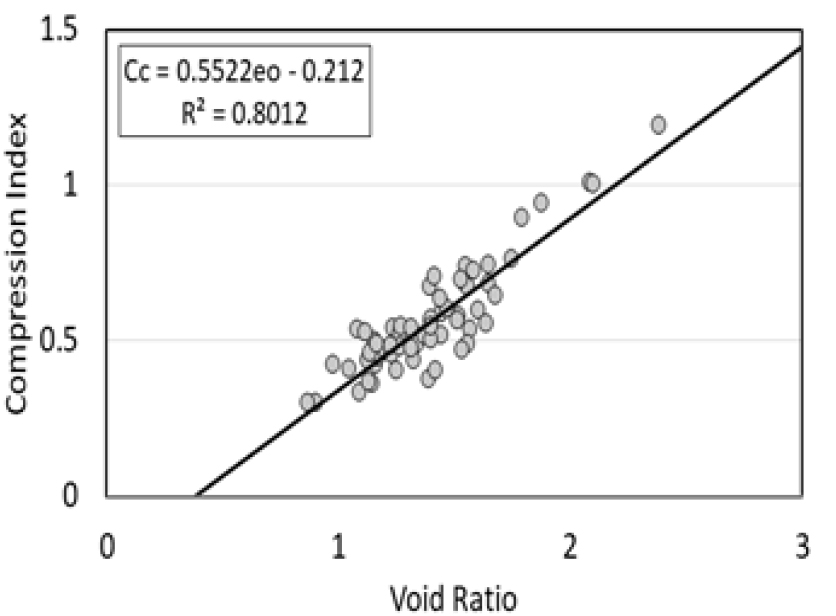
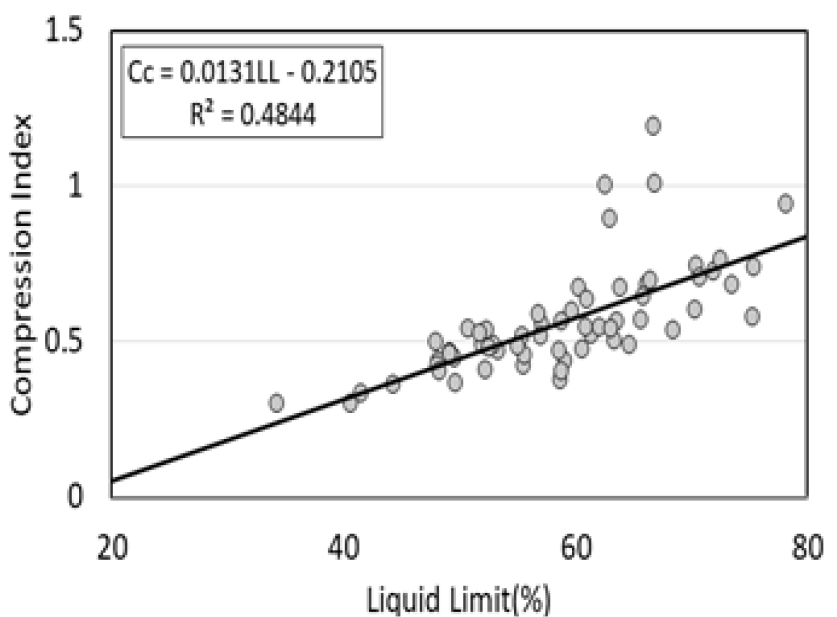
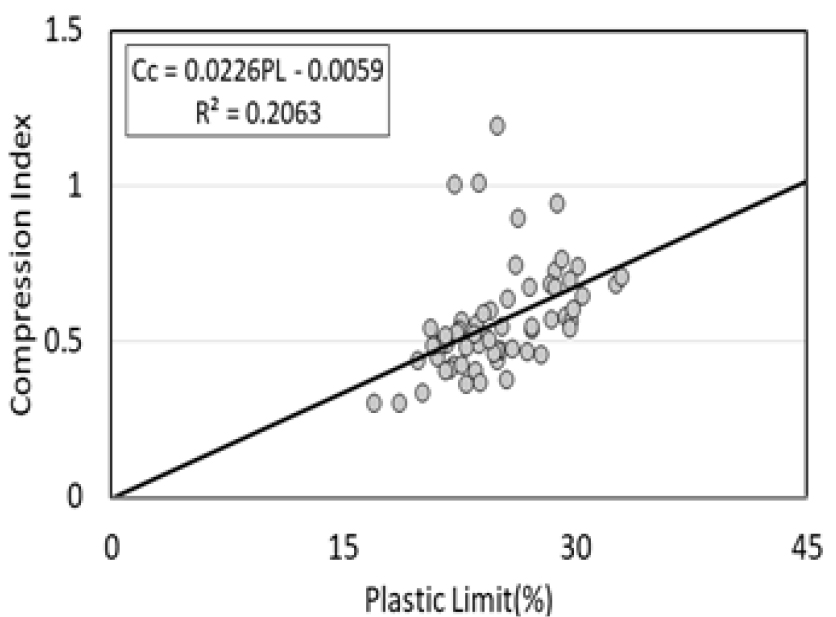
기계학습을 하기 전에 각 물리적 특성 값이 압축지수에 영향성을 가졌는지를 판단하기 위하여 먼저 엑셀을 이용하여 물리적 특성과 압축지수의 회귀분석을 진행하여 상관계수를 검토하였다. Fig. 1, 2, 3, 4의 그림은 각각 함수비, 간극비, 액성한계, 소성한계와 압축지수를 회귀분석한 후, 회귀분석 모형이 얼마나 적합한지에 대한 평가를 나타낸 그림이다. 물성 값별로 상관성에 차이는 있지만 각각의 점토 물리적 특성 값이 압축지수에 영향성을 가지고 있는 것을 알 수 있다.
Table 2는 Fig. 1, 2, 3, 4의 물리적 특성들과 압축 지수를 회귀 분석하여 나온 모델의 결정 계수 값과 상관 계수 값을 정리한 것이다. 결괏값을 보았을 때 함수비가 상관계수와 회귀 모델의 R2 값이 가장 높은 결과가 도출되었고 가장 낮은 값으로 소성 한계 값이 도출되었다. 함수비는 시료의 교란 여부와 관계없고 흙의 자연 상태 특성을 설명하기 때문에 오차율이 낮고 R2(R Squared) 값과 상관계수 값이 높게 나온 것으로 확인되는 반면 소성한계 및 액성한계는 각 지반의 상태에 따라 오차율의 변동이 있고 R2(R Squared) 값의 변동이 크다고 판단된다. 실제로 Kang et al.(2024)의 논문을 살펴보면 성토 이력이 없는 원지반 점토와 성토 이력이 있는 원지반 점토를 분석하였을 때 확연한 차이가 나타나는 것을 확인할 수 있었다. 본 연구에서는 상관성이 낮은 소성한계 및 액성한계도 기계 학습을 적용하여 데이터 분석을 할 경우 어느 정도 개선되는지 알아보고자 분석 대상에 포함하였다.
3. 기계학습 알고리즘 및 회귀모델 결과
3.1 오렌지 마이닝
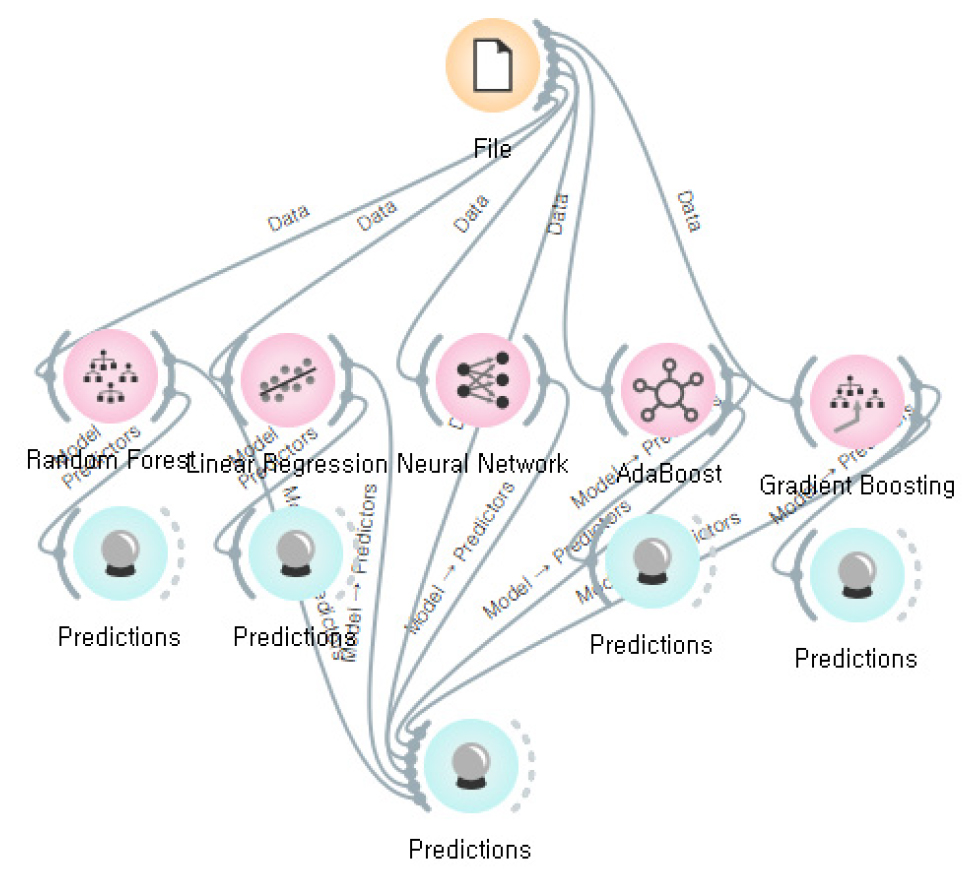
오렌지 마이닝은 슬로베니아 류블랴나 대학에서 개발한 인공지능으로 코딩 없이 데이터를 분석할 수 있는 프로그램으로 복잡한 코드를 사용하지 않고 위젯이라고 하는 컴포넌트들을 연결하여 손쉽게 지도 학습과 비지도 학습 인공지능을 구성할 수 있다(Kim et al., 2022). 오렌지 마이닝은 현재 교육용으로도 많이 사용되므로 편리성이 뛰어나고 사용자 인터페이스가 직관적이어서 데이터 로드, 전처리, 분석, 시각화 등의 과정을 쉽게 따라갈 수 있으며, Python이나 R의 경우 명령어를 모두 입력해야 하는 다소 복잡한 코딩을 필요로 하기 때문에 일반적인 연구자에게 다소 장벽이 있다. 이러한 장벽을 개선해 주는 프로그램이 오렌지 마이닝 프로그램이다(Lee, 2023). 본 연구에 사용하지 않은 다른 머신러닝 알고리즘을 지원하여 분류, 회귀, 군집화 등 여러 가지 데이터 분석 작업을 수행할 수 있다. 오렌지 마이닝은 Python, Cython, C++, C언어를 기반으로 작동하는 데이터 분석 프로그램으로, 만들어둔 데이터셋을 추가하여 머신러닝 모델을 적용한 후 예측하여 데이터 시각화를 보다 쉽고 간편하게 할 수 있는 프로그램이다. Fig. 5는 오렌지 마이닝 실행 예시이다.
3.2 기계학습 알고리즘
총 5개의 알고리즘을 연구에 사용하였다. 구체적으로 살펴보면 다음과 같다.
1) Random Forest
회귀 및 분류 문제를 다수의 Tree로 구성한 후, 이를 활용하여 최적의 결과를 도출하는 알고리즘으로 Bagging 기법의 대표적인 모델이다(Breiman, 2001). 주로 Yes or False의 결정을 일반화하여 선택해 나가기 때문에 독립 변수와 종속 변수 사이의 상관성이 높지 않아도 높은 정확도의 결과를 도출하는 장점이 있다.
2) Neural Network
머신러닝 기법 중 하나로 동물 뇌의 뉴런과 시냅스로 이루어진 신경망과 같은 구조로 구성된다. 시냅스로 이루어진 신경망과 같은 구조로 구성된다. 신경망의 분산적이며 병렬적인 정보처리 능력을 모사하여, 대량의 데이터를 학습하고 결과를 예측한다(Bak et al., 2024). Neural Network는 Input Layer, Hidden Layer, Output Layer이라는 3개의 층으로 구성되어 있으며 다층 구조와 활성화 함수를 통해 비선형성을 잘 처리할 수 있어 복잡한 패턴을 학습할 수 있다.
3) Linear Regression
선형 회귀 분석을 의미하며, 종속 변수와 독립 변수의 관계를 설명하는 기법으로 각각의 독립변수에 대해 기울기(가중치)와 절편을 산정하기 때문에, 유의성 및 설명력이 우수한 모델을 구축할 때 활용된다(Lee et al., 2022).
4) AdaBoost
앙상블 기법의 하나로, 여러 개의 약한 분류기를 결합하여 강력한 분류기를 만드는 기법이다. 모든 샘플에 같은 가중치를 할당하고 학습결과를 바탕으로 모형의 오차를 계산하여, 오차가 낮은 샘플에 대한 가중치를 감소시키고, 오차가 높은 샘플에 대한 가중치를 증가시킨다(Kim et al., 2023). 이러한 과정을 여러 번 반복하여 여러 개의 간단한 모델을 만든 후, 모든 모델의 예측을 합쳐 최종 예측을 만든다.
5) Gradient Boosting
Gradient Boosting은 학습 단계에서 예측된 모델 값에 대한 손실 함수를 Pseudo Residual을 기반으로 하여 이전 모형의 약점을 보완하는 새로운 모형을 순차적으로 적합한 뒤 이들을 선형 결합하여 얻어진 모형을 생성하는 지도 학습 알고리즘이다(Guo et al., 2018).
위 다섯 가지 모델들은 데이터 예측 및 분석을 하는 대표적인 알고리즘으로 그중 AdaBoost와 Gradient Boosting의 경우 같은 예측 성능을 향상시키는 모델이지만 서로 오차를 향상시키는 방식에 차이가 있어 선정하게 되었다. Random Forest 알고리즘의 경우에는 Bagging이라는 모델로 결과를 나타내는 알고리즘으로 예측 모델에 대표적인 모델이다. Neural Network는 복잡한 패턴 인식에 강한 모델로 여러 데이터를 예측하고 결과를 도출하는데 많이 사용되는 모델이므로 본 연구에 모델로 선정하게 되었다.
3.3 회귀 모델 결과
부산항 신항의 물리적 특성 값을 회귀 모델에 적용한 결과를 Table 3에 정리했다. R2(R Squared) 값이 AdaBoost 모델에서 가장 높은 값을 나타냈고 Linear Regression 모델에서 가장 낮은 값을 나타냈다. 오차율 또한 AdaBoost 모델에서 가장 낮은 값을 나타내는 것을 확인할 수 있는데, 그 이유는 많은 데이터를 분석하는데 예측이 잘 이루어지지 않은 데이터에 많은 중요도를 부여하여 다음 데이터를 예측하며 조금씩 오차율을 줄이며, 최종적으로 앞서 분석한 데이터의 예측을 종합적으로 합쳐 최종 예측을 생성하기기 때문에 가장 오차율이 적고 적합한 모델이 형성되었다고 판단된다.
Table 3.
Machine learning application results by model
함수비와 간극비의 경우 모든 기계학습 모델에서 R2 값이 유의미함을 나타내지만 액성한계와 소성한계의 경우 Neural Netwok와 Linear Regression 모델에서 R2(R Squared) 값이 다른 모델에 비해 많이 낮은 것이 확인이 되었다. Neural Network의 경우 복잡한 비선형 관계를 모델링 하는데 적절하지만 입력 데이터가 적어 명확하게 학습되지 않고 여러 이상치 값들이 포함되어 있어 R2(R Squared) 값이 정확한 값을 나타내지 못하는 것으로 예상된다. 추후 연구에서는 입력 데이터를 충분히 확보한 상태에서 최적의 하이퍼파라미터를 설정하여 모델에 적용시키는 방법이 필요할 것으로 생각된다.
앞서 했던 함수비 Linear Regression의 결과와 비교해 봤을 때 기계학습을 적용시켜 데이터를 분석한 값이 회귀 분석을 한 값보다 오차율이 낮을 뿐만 아니라 R2(R Squared) 값 또한 더 높은 수치를 나타내는 것을 확인할 수 있다. 그리고 회귀 분석을 하였을 경우 RMSE 값이나 MAPE 값과 같은 오차율을 나타내는 지표를 확인하기 위해서는 여러 계산식을 사용해야 하지만 기계학습을 적용하여 분석을 할 경우 더 간편하고 한눈에 알아볼 수 있게 나타나는 것을 보아 편리성 또한 회귀 분석보다 더 뛰어나고 유용하게 사용될 수 있을 거라 예상된다.
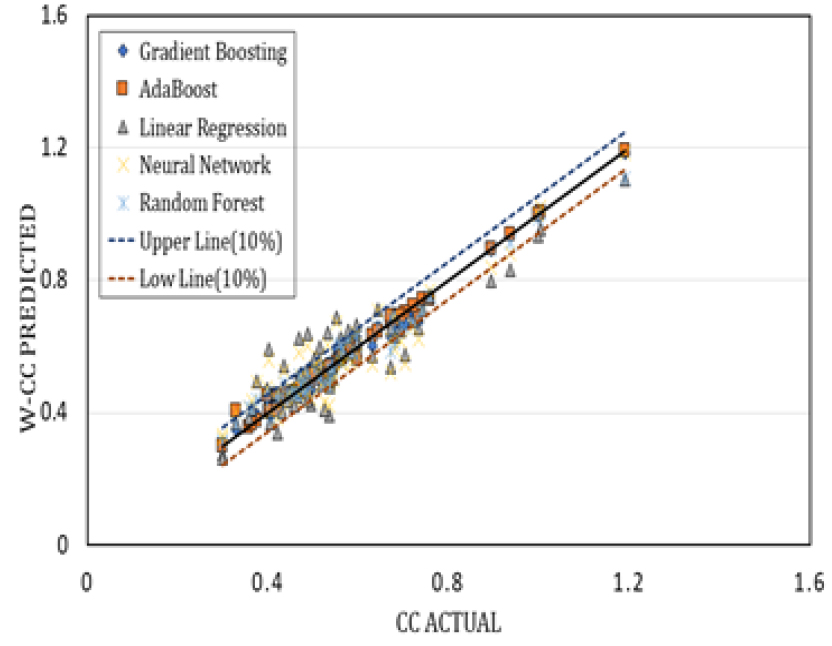
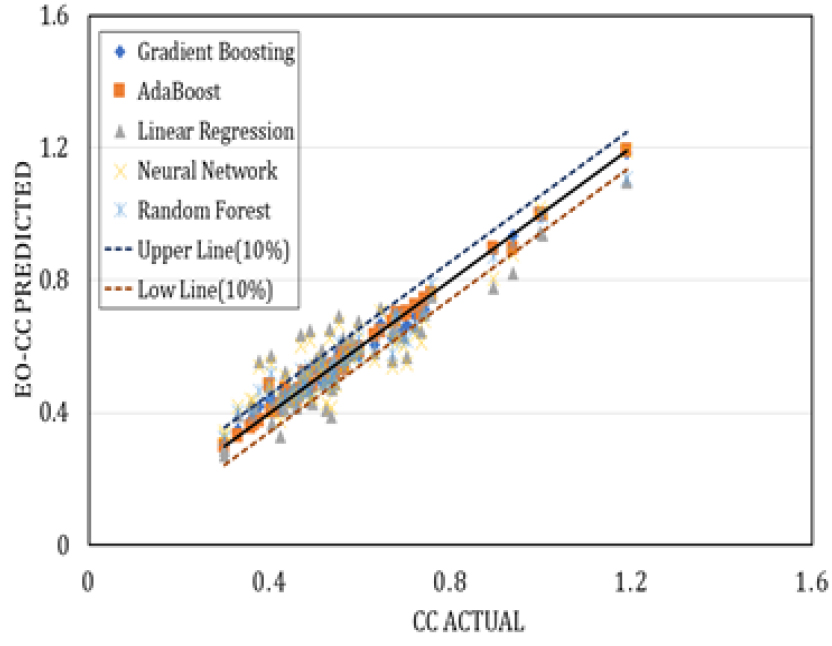
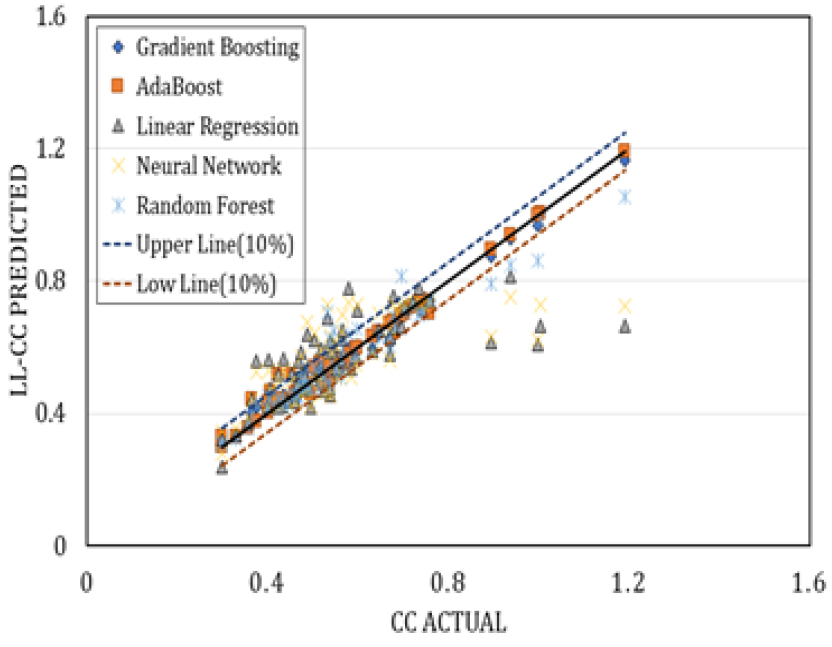
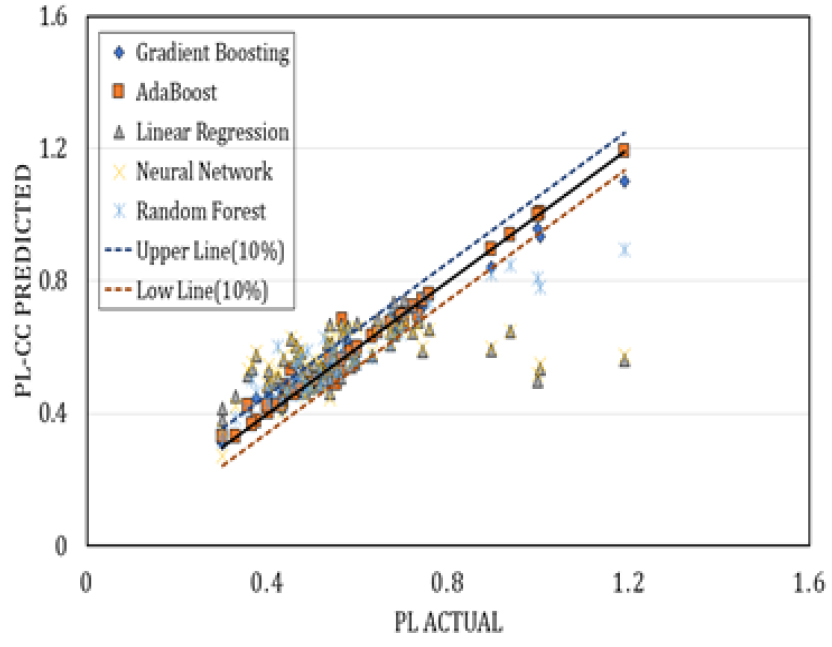
Fig. 6, 7, 8, 9 은 각각의 모델을 적용하여 나온 예측값을 표본의 압축지수와 비교하여 나타낸 그래프이다. Linear Regression 모델과 Neural Network 모델의 경우, 다른 기계학습 모델과 비교했을 때 많이 분산되어 있는 것을 확인할 수 있다. 물리적 특성들을 회귀 분석 한 결과를 살펴보았을 때, 함수비가 가장 이상적인 결괏값을 도출해 내는 걸로 보아 압축지수를 예측하는 데 가장 적합한 특성이라 판단하였다. 함수비와 압축지수를 회귀분석하였을 때 오차율은 11%가 도출되었다. 그러므로 본 연구에서는 예측값의 상한선과 하한선을 표본의 평균값의 10%가 적당한 기준이라고 생각하여 상한선과 하한선으로 적용하였다.
4. 회귀모델 평가기준
보통의 기계학습 회귀 모델의 평가 기준으로는 오차율을 나타내는 지표 중 하나인 RMSE(Root Mean Squared Error) 값과 결정 계수인 R2(R Squared) 값을 주로 사용한다. 하지만 본 연구에서는 각 모델 RMSE 값이 아주 미세하게 차이가 나며 각 모델에 대한 오차율과 상관성을 분석하는 데 큰 영향을 주는 것으로 보기 힘들어 회귀 모델 오차율을 나타내는 또 다른 지표인 MAPE(Mean Absolute Percentage Error) 값을 함께 제시하기로 하였다.
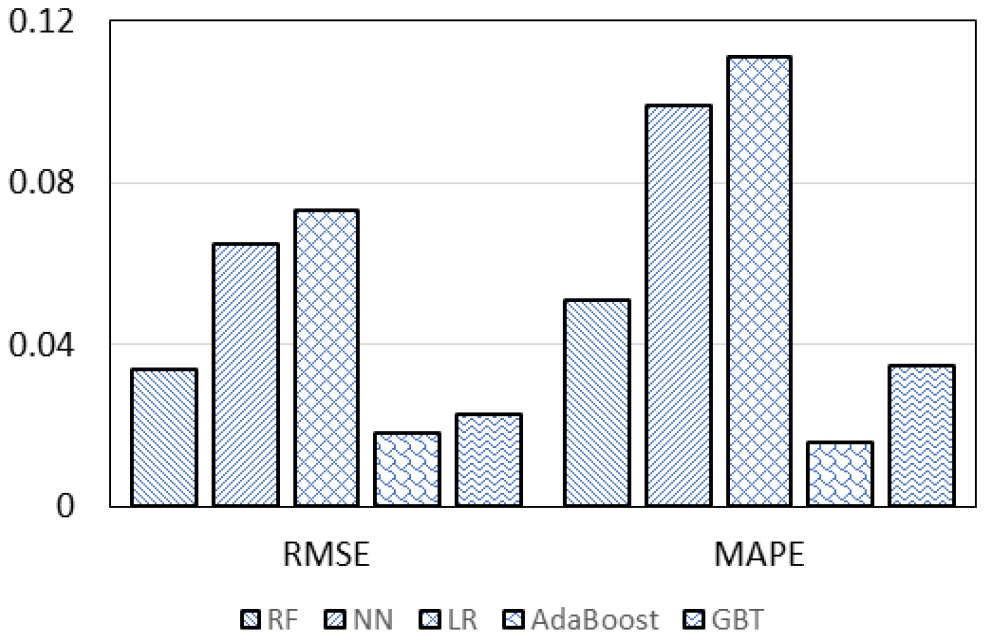
Table 3의 함수비 결과를 이용하여 RMSE 값과 MAPE 값을 비교했을 때, Fig. 9와 같이 MAPE 값이 RMSE 값보다 구분하기 수월한 것을 확인할 수 있다. 여기서, MAPE 값은 예측 값과 표본 값 사이의 절대 백분율 오차의 평균을 나타내는 값으로, 모델의 정확도를 평가하는 지표이다. 또한, 적합성을 판단하는 결정 계수 R2(R Square) 값을 표시하여 기계학습 모델들의 상관성을 분석하고 예측하는 최적의 모델을 선정하고자 하였다.
Fig. 10은 RMSE와 MAPE 값을 비교하기 위한 그림이다. 원활한 비교를 위해 가장 오차율을 잘 나타낼 수 있는 함수비와 압축지수를 각 모델에 적용하여 회귀분석한 데이터 결과를 이용하여 분석하였다.
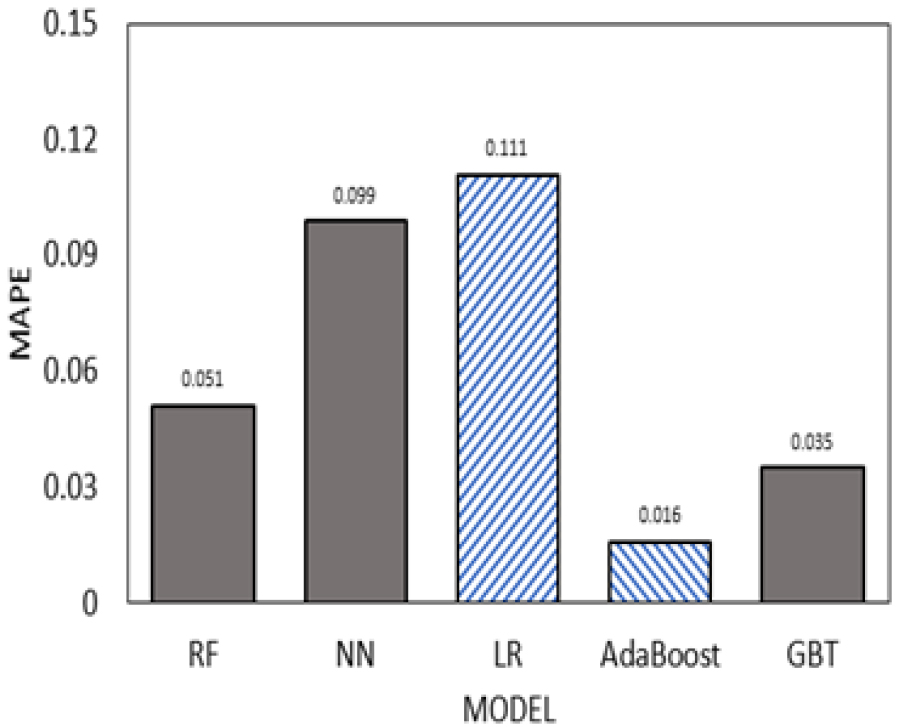
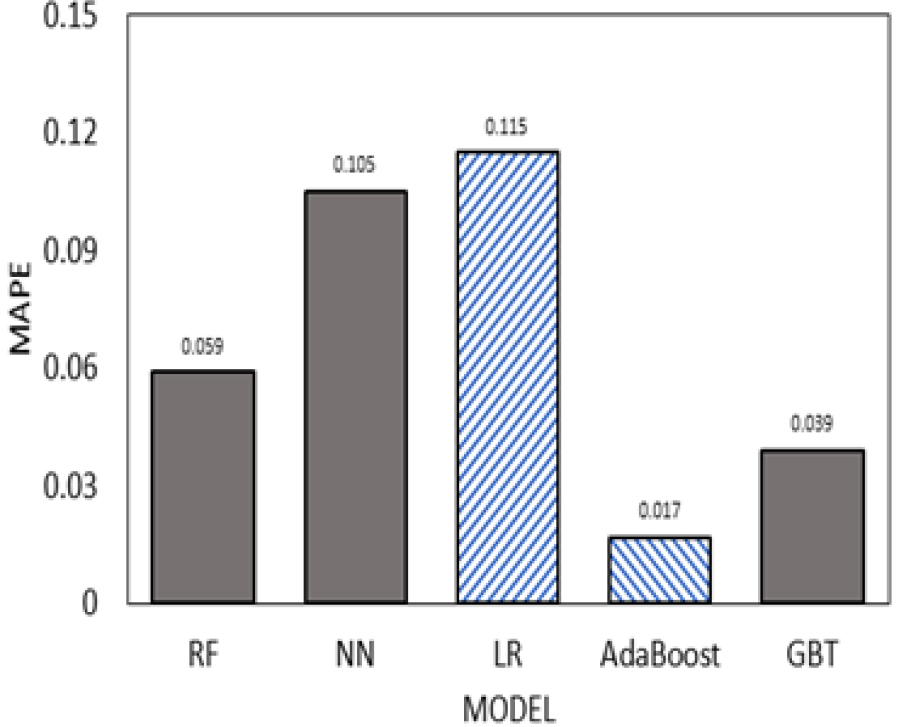
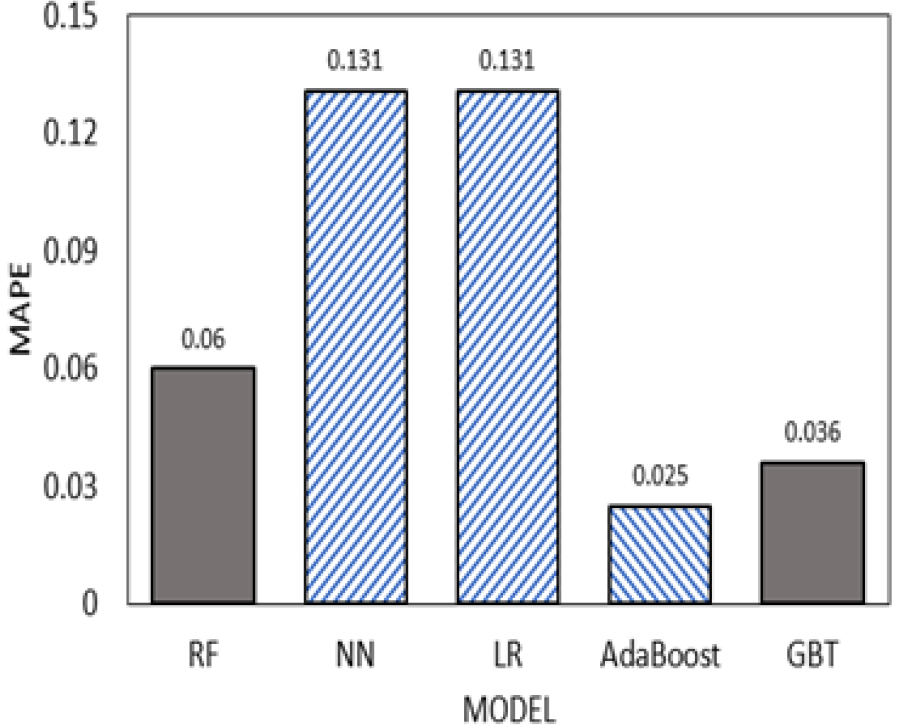
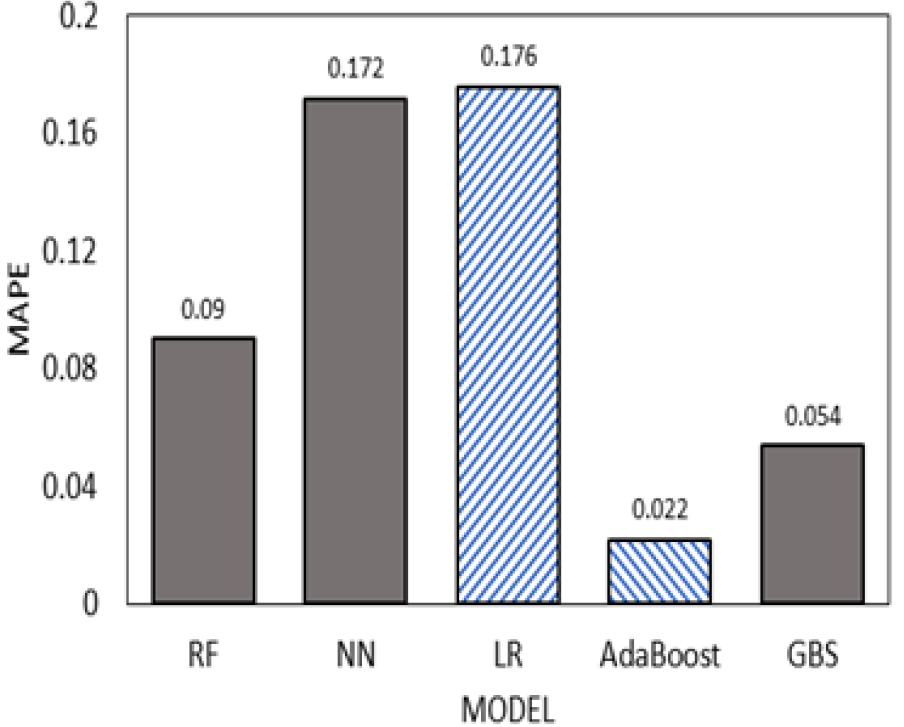
Fig. 11, 12, 13, 14는 모델별 MAPE 값을 시각화한 그림이다. 모델별 MAPE 값은 AdaBoost모델이 오차율이 가장 낮고 R2(R Squared) 값이 가장 높게 나왔다. 이 수치들을 종합적으로 보면 Linear Regression을 사용 하는 것보다 기계학습 모델을 적용하여 회귀분석을 했을 경우 모델의 적합성이 더 높게 나오고 오차율이 낮게 나오는 것을 알 수 있다.
5. 결 론
연약지반에서 지반 침하량 예측은 매우 중요한 변수이다. 침하량을 예측하기 위해서는 적합한 압축지수 값을 선정하여야 하는데 현장에서 실험을 통해 압축지수 값을 얻어내는 것은 많은 어려움이 있다. 본 연구에서는 기계학습을 통한 여러 회귀 분석 모델을 적용하여 압축지수 예측값을 찾아내는 데 최적화된 모델을 찾고자 하였으며 여러 모델을 회귀 분석했을 때 나오는 오차율과 R2(R Squared) 값을 이용하여 증명하였다. 구체적으로 다음과 같은 결론을 도출하였다.
Linear Regression을 사용하는 것보다 기계학습을 적용하여 회귀분석을 했을 경우 모델의 적합성이 더 높게 나오고 오차율이 낮게 나왔다. 구체적으로 결과를 살펴보면 함수비를 이용하여 압축지수를 예측하는 모델이 R2(R Squared) 값이 높게 도출되었고 오차율이 가장 낮게 도출된 반면, 소성한계를 이용한 모델에서는 R2(R Squared) 값이 다소 낮게 보이며 오차율이 다른 모델에 비해 크게 도출되는 것을 확인할 수 있었다. 그리고, 각 모델별로 결과를 도출하여 확인한 결과 Neural Network 모델은 데이터 셋이 불규칙할 경우 다른 기계학습 모델에 비해 오차율이 높고 R2 값이 낮게 도출되었으며, AdaBoost 모델은 오차율이 가장 낮고, R2(R Squared) 값은 가장 높게 도출되어 예측 값을 얻는 것에 최적화된 모델이라고 생각된다. 그 이유는 AdaBoost의 경우 앞서 분석한 모델들의 오차율을 기준으로 가중치를 조정하여 다음 모델에 적용하고, 오차율을 줄여나가며 최종적으로 모든 분석 모델들의 결과를 종합하여 최적의 결과가 나타내기 때문이다. 따라서 향후 지반공학과 관련된 데이터 분석에서 AdaBoost 모델의 적용이 가능할 것이다.