1. 서 론

말뚝 기초는 선단지지력과 말뚝 주면 사이에서 발생하는 주면 마찰력에 의해서 지지되는 지반구조물로서 시공 방법에 따라서 다양하다. 기존 말뚝은 소음과 진동 문제(항타 말뚝), 환경적인 문제(현장타설말뚝)를 야기한다. 국내외에서는 이러한 문제점들을 극복하고자 새로운 형태의 말뚝 기초가 제안되어 오고 있다. 국내에서는 기존 강관에 나선 형상의 헬릭스를 부착한 헬리컬 파일에 대한 연구가 활발히 진행되어 오고 있다(Lee et al., 2017; Bak et al., 2018; Bak et al., 2019; Bae et al., 2020). 회전 관입기로 헬리컬 파일 선단부에 회전력을 가하면, 회전력은 헬리컬 파일의 중심축을 따라서 헬릭스에 전달되고, 지반의 전단저항보다 커지면서 헬리컬 파일의 시공은 이루어진다. 이로 인해서, 기존 말뚝 시공 과정에서 필요한 천공을 위한 선행 굴착, 콘크리트 타설, 그리고 항타 공정이 필요가 없다(Lee et al., 2014).

국외에서는 최근 지반공학 문제에서 효율적인 설계와 성능 향상에 대한 필요성이 커지면서, 생물의 특성으로부터 영감을 받은 생물학적 모방 기술(bio-inspired technology)이 크게 주목받고 있다. 뱀은 이동시에 복부 비닐과 지면 사이의 경계면 마찰을 최소화하고, 정지 시에 경계면 마찰을 최대화하므로서, 이동 방향에 따라서 마찰을 선택적으로 이용한다. 이러한 호의적인 전단 저항(Favorable friction resistance)을 이용한 새로운 말뚝 형태를 개발하여, 말뚝의 주면 마찰을 증가시킬 뿐만 아니라, 기존에 지반 처리 및 개량에서 주로 사용된 시멘트를 줄이므로 크게 각광을 받고 있으며, 기초 연구가 활발히 진행되어 오고 있다(DeJong et al., 2017; Martinez et al., 2019; Stutz et al., 2019; Martinez et al., 2020; O’Hara and Martinez, 2020; Martinez and O’Hara, 2021).

우선, 흙과 뱀 비닐에서 영감을 받은 플레이트에 대한 경계면 마찰 이방성을 정량적으로 평가하기 위한 연구가 선행되어 왔다. 뱀 비늘의 기하학적 형상을 모방한 표면 돌출부를 갖는 플레이트는 3D 프린터를 이용하여 정밀하게 제작하고, 수정된 직접 전단 시험기를 이용하여, 다른 초기 수직 응력과 양방향 전단 조건에서 표면 돌출부-모래 경계면에서 발생되는 전단 거동을 분석하였다. 표면 돌출부 길이 L가 짧을수록, 돌출부 높이 H가 높아질수록 전단 강도는 증가하였으며, 일정한 돌출부 형상 조건에서 cranial shearing direction(전단 시 돌출부 높이가 감소하는 방향)이 caudal shearing direction(전단 시 돌출부 높이가 증가하는 방향)보다 더 큰 최대전단강도와 잔류강도 그리고, 경계면 마찰각을 정량적으로 평가하였다(Lee and Chong, 2022; Lee et al., 2023). 또한, Nawaz et al.(2024)은 둥근 입자(rounded particle) 보다 모난 입자(angular particle)에서 더 높은 경계면 팽창 거동과 마찰을 확인하고, 경계면 마찰각과 팽창각에 대한 경험식을 제안하였다. Martinez et al.(2019)은 경계면 직접 전단시에 입자 영상 속도 측정(particle image velocimetry)을 이용하여 전단 파괴모드를 분석하였다. 그 결과, cranial 방향으로 전단 시 돌출부 사이에 위치한 흙이 수동 상태로 존재하며, 이로 인해서 돌출부 형상과 유사한 형태의 쐐기(wedge)모양을 형성하고, 이와 반대로 caudal 방향으로 전단 시 균일한 변형을 가진 전단 밴드(shear band)를 형성하는 것을 확인하였다.

Kim et al.(2024)는 뱀 비늘에서 영감을 받은 돌출 표면 형상을 갖는 콘의 하중 방향에 따른 경계면 마찰 이방성을 평가하기 위해서, 콘의 하중 방향(관입 → 인발)에 따른 콘 전단 저항과 관입 깊이를 정량적으로 평가할 수 있는 실내 모형 토조와 소형 콘 시스템(Miniature Cone System)을 개발하였다. 직접전단실험결과와 유사하게, 돌출부 높이가 높을수록, 돌출부 길이가 좁을수록, 그리고 돌출부 높이가 감소하는 cranial 관입 방향으로 더 큰 콘 관입 저항을 보였다. 이와 같이, 기존 연구에서는 경계면 직접전단 시험과 실내 콘 관입 실험을 통하여, 경계면 전단 저항의 증가를 정량적으로 확인하였다. 하지만, 돌출부를 갖는 말뚝과 주변 흙 사이에서 발생하는 주면 마찰력 거동 특성에 대한 분석은 전무한 실정이다.

본 연구에서는 돌출부 표면을 갖는 콘 관입 과정을 모사하기 위하여 ABAQUS에 내장된 대변형 해석 기법인 Coupled Eulerian-Lagrangian(CEL) 기법을 사용하여, 돌출부 표면의 기하학적 형상에 따른 콘 관입 하중 변화에 대한 수치해석 연구를 수행하였다. 우선, 콘과 콘 주변 메쉬에서 발생하는 수치해석 오차를 최소화하기 위해서, 콘과 주변 지반에 3차원 일반화된 메쉬를 제안하였다. 제안된 메쉬를 이용하여 돌출부 표면의 기하학적 매개변수 해석에 따른 하중 거동을 정량적으로 분석하였다.

2. Coupled Eulerian-Lagrangian(CEL) 기법을 이용한 콘 관입 수치해석 모듈 개발

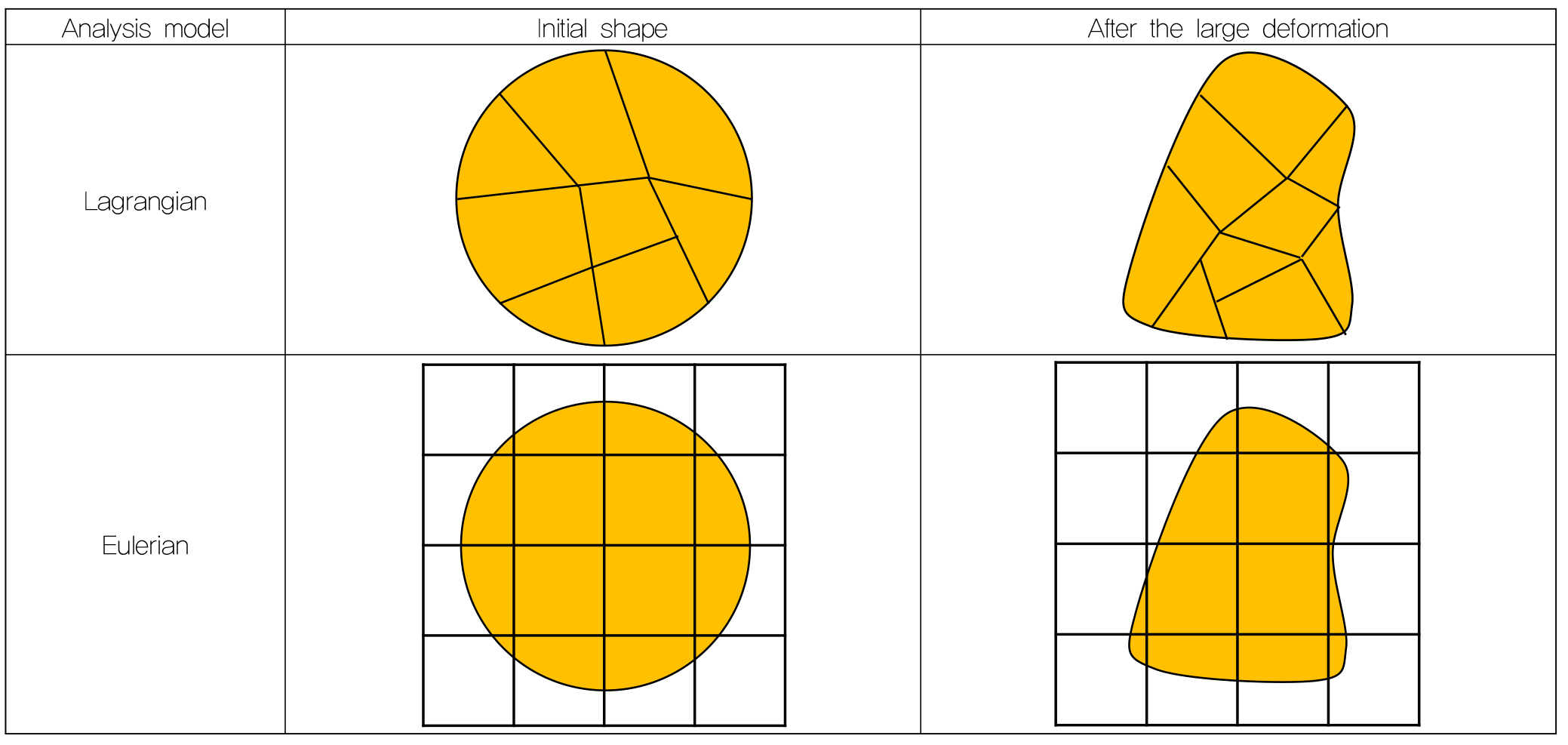
유한요소해석법(Finite Element Method, FEM)에서 체적을 가지는 요소의 시간에 따른 거동을 모사하는 방법은 크게 Lagragian 해석법과 Eulerian 해석법이 있다(Fig. 1). 일반적으로 고체역학에 적용되는 Lagrangian 해석법은 각각의 요소의 물성 좌표와 시간에 대한 함수로 연속체의 거동을 정의하며, 물체의 초기 형상을 기준으로 각 요소의 물성이 절점과 함께 이동하며 변형을 분석한다. 하지만, 대변형 시 접촉면 또는 일부 요소의 왜곡으로 인해 계산의 정확성과 수치해석 안정성(numerical stability)에 영향을 준다. 반면, Eulerian 해석법은 연속체의 거동을 고정된 공간 좌표와 시간의 함수로 정의하며, 물체의 거동이 전체 영역내에서 물질의 이동량으로 결정되므로, 메쉬의 왜곡이 발생하지 않는다. 따라서, Lagrangian 해석법과 Eulerian 해석법의 장점을 결합한 Coupled Eulerian-Lagrangian(CEL)기법을 이용하여, 산사태 토석류 거동분석(Jeong et al., 2015)과 항타 관입 말뚝(Ko et al., 2015) 같은 대변형이 발생하는 지반구조물 수치해석에 활발히 적용하고 있다.

Fig. 1.

Mesh deformation of a continuum (Qiu et al., 2011)

2.1 유한 요소 메쉬 모델링(Finite Element Mesh Modeling)

상용 유한 요소 프로그램인 ABAQUS 6.14를 사용하여, 표면 돌출부를 갖는 콘의 기하학적 형상에 따른 콘 관입 하중 변화를 정량적으로 평가하였다. 콘 두부에 일정한 하중이 가하였을 때, 시간에 따른 관입깊이와 주변 지반의 거동을 분석하기 위해서 Explicit dynamic 해석을 수행하였다.

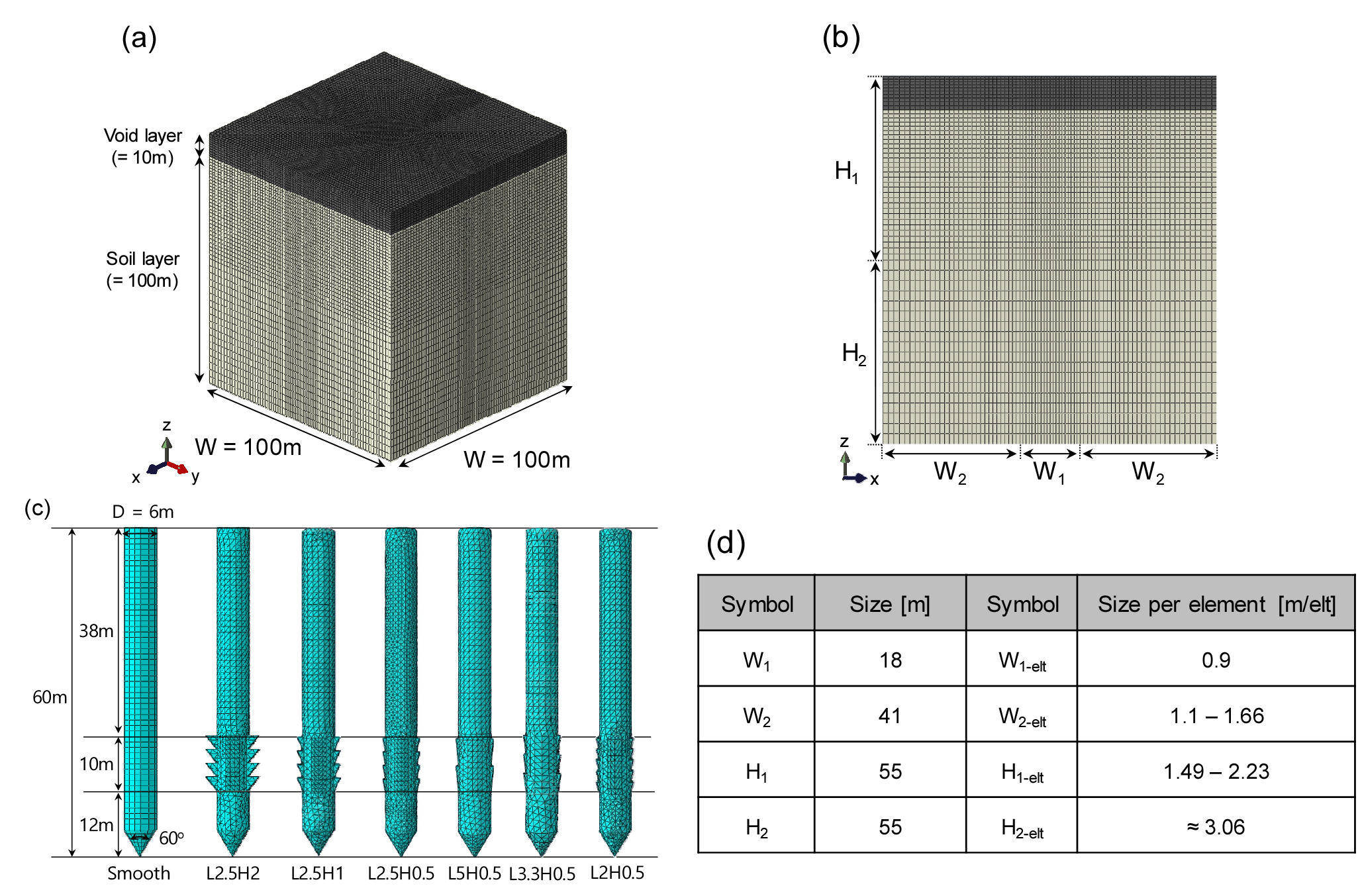
일반적으로 Mesh 모델링은 수치해석의 정확성과 소요 시간에 직접적인 영향을 미친다. 특히, 콘이 관입될 요소들의 불규칙한 mesh는 잘못된 하중 분포와 관입 저항을 야기할 수 있다. 본 연구에서는 프로그램에 내재된 Hex-structured mesh 기능을 활용하여 콘이 관입될 요소들에 일정한 mesh로 형성하였다. Fig. 2는 전체 해석 도메인에서 콘과 콘 주변에 생성된 mesh를 보여준다. 전체 해석 도메인의 크기는 100m×100m×110m이며, 반무한 공간을 구현하기 위해 콘 관입 지점과 경계면과의 충분한 거리를 확보 하였다(Fig. 2(a)). 도메인은 상부 10m에 물성이 정의되지 않는 void layer와 하부 100m에 물성이 정의되어 있는 soil layer로 구성하였다. Void layer는 콘 관입 시 상부 지반 mesh의 변형과 이동으로 인해 발생할 수 있는 경계효과를 방지하기 위해 형성하였다. 또한, Void layer과 soil layer는 콘 관입 시에 대변형 해석을 위해 Eulerian 해석법을 적용하였다. Fig. 2(b)에서 보이는 바와 같이, 너비 W는 2개의 부분(W₁와 W₂)으로 나누었다. W₁은 콘이 관입되는 영역으로, 주변 지반 거동을 정확히 분석하기 위해 요소당 크기를 0.9m/element(이하 m/elt)로 조밀하게 구성하였다. W₂는 수치해석에 소요되는 시간을 줄이기 위해 등비수열을 이용하여 최소 1.1m/elt에서 최대 1.66m/elt로 메쉬 크기를 조절하였다. 깊이 H는 H₁과 H₂로 구성되었다. H₁은 너비 방향의 요소들과 동일하게 0.9m/elt에 가까운 조밀한 요소당 크기로 형성하였고, H₂는 3m/elt에 가까운 크기를 가진 느슨한 요소들로 구성하였다. 일반화된 메쉬는 Fig. 2(d)에 정리하였다. Fig. 2(c)는 모델링에 사용된 7개의 다른 콘(표면이 부드러운 콘 1개와 표면 돌출부의 길이와 높이가 다른 6개)을 보여준다. 모든 수치해석에서 사용된 콘은 직경 D 6m, 전체 길이 60m, 그리고 선단각은 60°의 내부가 채워진 형태로 구성되었다. 표면 돌출부는 콘 선단으로부터 직경의 2배(2D = 12m) 위치에 설치하였으며, 돌출부의 전체 길이는 10m로 일정하게 형성하였다. 콘과 콘 주변 지반 사이의 경계면 마찰 해석을 수행하기 위해서 콘에는 Lagrangian 해석법을 설정하였다.

Fig. 2.

Generated mesh and generalized mesh size proposed in this study: (a) generated mesh on the 3D domain; (b) front view; (c) textured cones; (d) generalized mesh size

2.2 경계 조건 및 입력 물성치

콘은 지반 모델의 연직 방향 콘 관입을 위해서 x방향과 y방향을 구속하여 z방향으로의 변위만을 허용하였다. 지반 요소의 측면 경계조건은 z방향으로만 변위를 허용하기 위해 롤러구속조건을 적용하였으며(x방향과 y방향의 변위가 발생하지 않도록 고정함), 하부 경계면에는 Encastre로 구성하여 모든 축방향의 변위가 발생하지 않도록 구속하였다. 콘은 탄성으로 모델링하였고, 지반은 항복 응력과 소성 변형이 발생하는 시점의 변형률만으로 구현되는 Elasto-Perfectly plastic 모델을 이용하였다. 수치해석에 적용된 콘과 지반 요소는 8개의 절점(node)을 가진 육면체로 나타내었다(Lagrangian brick 요소와 Eulerian brick 요소인 C3D8R, EC3D8R을 각각 적용함). 콘 관입시 발생하는 콘과 지반 사이의 경계면 마찰은 Tangential behavior 기능에 내재된 완전 접촉 조건(constraint-rigid body)으로 설정하였으며, 마찰계수는 0.385로 입력하였다. 일반적인 접촉 요소(contact element)는 정적해석 시 두 접촉면을 지정하는 해석 알고리즘(접촉면 해석방법)을 적용하지만, 본 해석과 같은 CEL 해석에서는 시간에 따라 접촉면이 유동적이므로 ABAQUS에서 제공하는 general 접촉 알고리즘을 적용한다. 이는 Lagrangian 요소와 Eulerian 요소간의 접촉면 mesh가 일치하지 않아도 되며, 시간에 따라 경계면이 자동으로 계산이 되므로 경계 부분의 mesh 크기에 따라 경계면 부근의 해석 결과가 다르게 나타날 수 있다. 수치해석에 사용된 모델 물성치를 Table 1에 정리하였다. 또한, 본 연구에서는 7개의 다른 콘(표면이 부드러운 콘 1개와 표면 돌출부의 길이와 높이가 다른 6개)과 2개 관입 방향(Cranial 방향 – 관입시 돌출부 높이가 감소하는 방향; Caudal 방향 – 관입시 돌출부 높이가 증가하는 방향) 조건으로 총 13 케이스에 대해서 해석을 수행하였다(Table 2). 콘 관입 해석은 콘 두부에 하중제어를 수행하고, 일정한 하중을 점진적으로 증가시키는 조건에서 관입 깊이를 도출하였다. 해석 결과는 관입 깊이에 따른 관입 하중 변화로 도시하였다.

3. 표면 돌출부의 기하학적 특성과 하중 방향에 따른 관입 저항 변화

3.1 수직 유효응력: 예비 수치해석

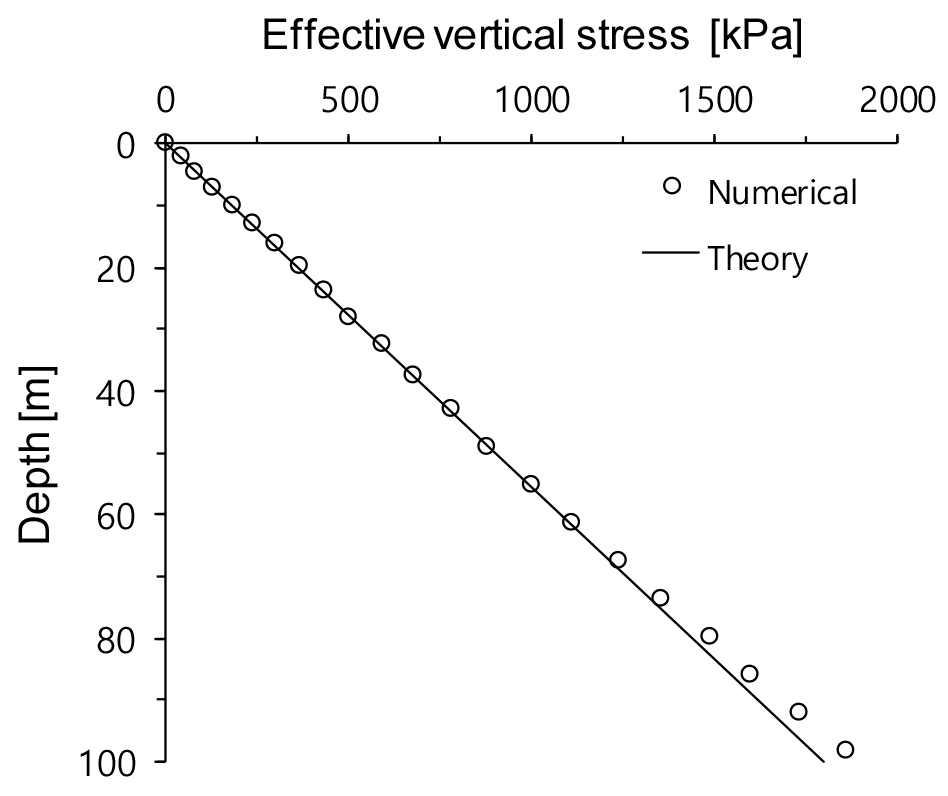
콘과 콘 주변에 본 연구에서 제안된 정량화된 mesh를 적용하고, 지반에 Geostatic 조건을 적용한 상태에서 예비 수치해석을 수행하였다. Fig. 3은 깊이에 따른 흙의 유효수직응력을 보여주고 있다. 예상한 바와 같이, 깊이가 깊어질수록 수직응력은 일정하게 증가하였으며, 70m 까지는 이론식과 매우 유사한 수직응력을 보였지만, 그 이후에는 차이를 보였다. 이는 콘이 관입이 끝나는 지점(약 50m) 이후에는 수치해석에 소요되는 시간을 줄이기 위해 등비수열을 이용하여 메쉬를 느슨하게 모델링하였기 때문이다. 이와 같이, 예비 수치해석 결과를 통해서 본 연구에서 개발한 표면 돌출부를 갖는 콘의 수치해석 모듈의 신뢰성을 검증하였다.

Fig. 3.

Comparison of effective vertical stress with depth

3.2 표면 돌출부의 기하학적 특성과 하중 방향에 따른 매개변수 해석

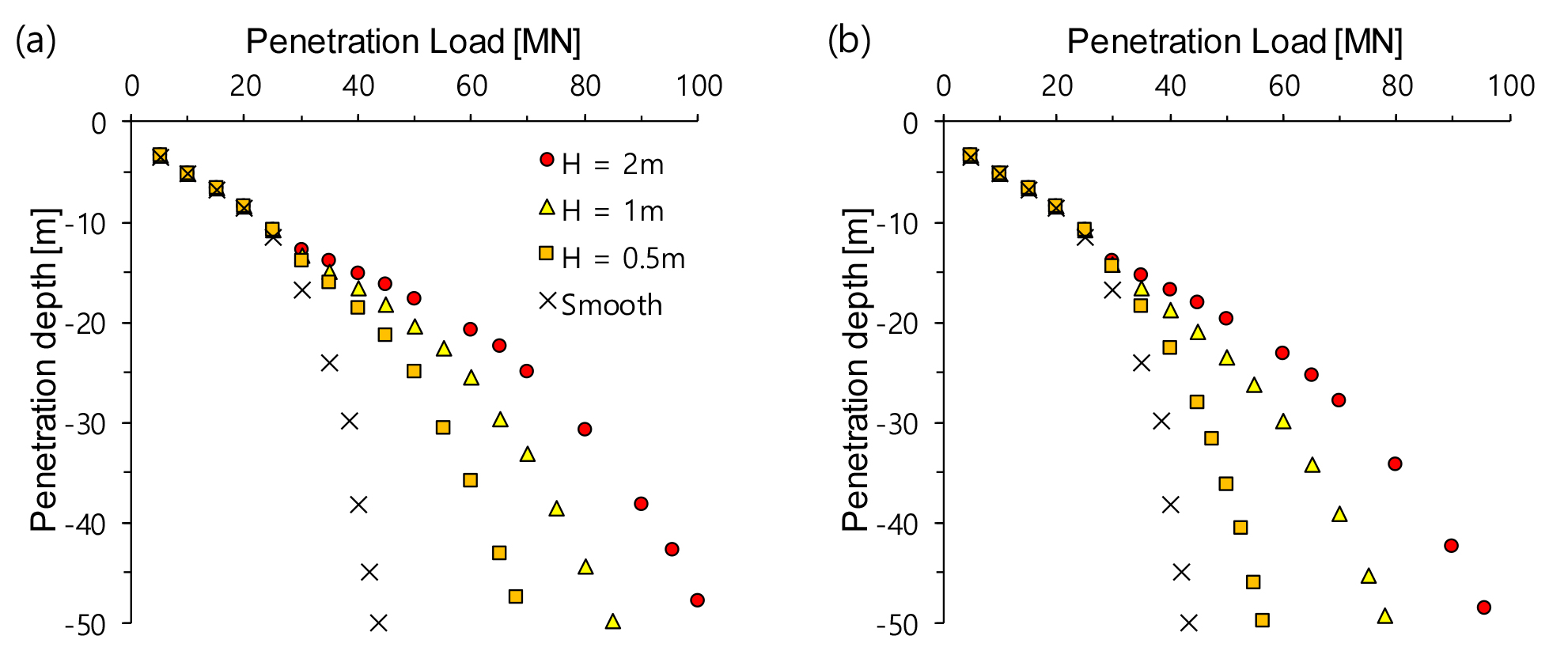
Fig. 4는 동일한 표면 돌출부 길이 조건(=2.5m)에서 표면 돌출부 높이 H에 따른 관입 하중 변화를 보여준다. 표면 돌출부 높이와 하중 방향에 관계없이 특정 관입 깊이(=12m)까지는 표면 돌출부가 없으므로 관입 하중에 차이가 미비하였지만, 이후 관입 깊이(>12m)부터는 표면 돌출부 형상과 하중 방향에 따라서 관입 깊이 차이가 뚜렷하게 나타났다. 동일한 관입 하중(=45MN)에서 표면 돌출부를 갖지 않는 콘은 약 50m 관입하였지만, 표면 돌출부를 갖는 콘은 얕은 깊이까지만 관입되었다. 동일한 하중(=45MN)과 하중 방향(=cranial direction)에서 표면 돌출부 높이 H가 증가함에 따라 관입 깊이는 더욱 얕아졌다(H = 0.5m에서 21.3m이고, H = 1m에서 18.3m, 그리고 H = 2m에서 16.3m) (Fig. 4(a)). 또한, 모든 조건에서 cranial 하중 방향이 caudal 하중 방향에 비해 얕은 깊이까지 콘 관입이 되었고, cranial 하중 방향과 caudal 하중 방향 간의 관입 깊이 차이는 표면 돌출부 H가 작아질수록 더욱 크게 나타났다(H = 2m인 경우에는 관입 깊이 차이는 1.82m이고, H = 1m에서 2.66m, 그리고 H = 0.5m에서 6.79m).

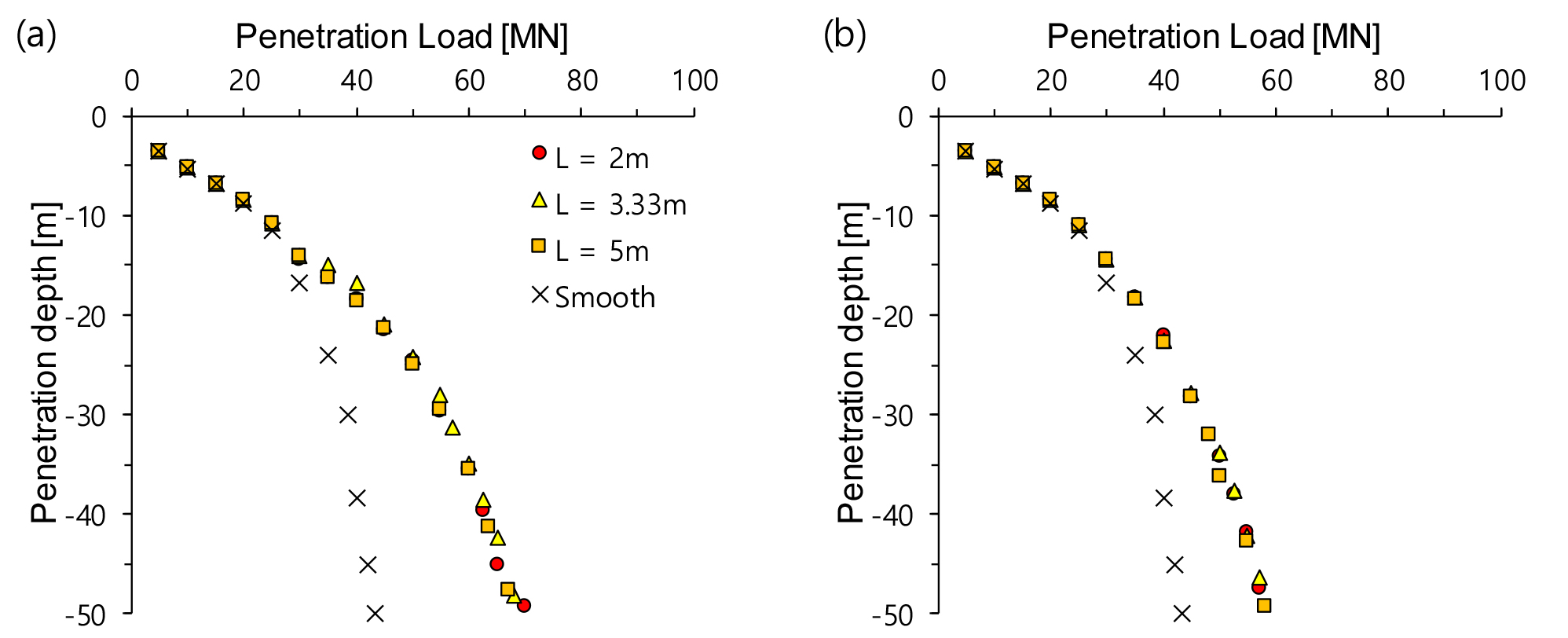
Fig. 5는 표면 돌출부 높이 H(= 0.5m)가 일정한 조건에서 표면 돌출부 길이 L에 따른 결과를 보여주고 있다. 우선, 동일한 관입 하중 방향에서 돌출부 길이 L에 따른 관입 깊이 차이는 거의 미비하였다. 하지만, 표면 돌출부 높이 H에 따른 하중 변화 결과와 유사하게 동일한 관입 하중 조건(= 45MN)에서 caudal 하중 방향보다 cranial 하중 방향에서 더 얕은 깊이까지 관입이 발생하였다. 또한, 표면 돌출부 L에 따른 cranial 하중 방향과 caudal 하중 방향 간의 관입 깊이 차이는 표면 돌출부 높이 H에 비해서 더 큰 차이를 보였다(L = 2.5m에서 6.5m이고, L = 5m에서 7.22m, 그리고 L = 10m에서 9.98m).

Fig. 4.

Variation in penetration load according to scale height: (a) cranial penetration direction; (b) caudal penetration direction. The scale length is fixed as 2.5m

Fig. 5.

Variation in penetration load according to scale length: (a) cranial penetration direction; (b) caudal penetration direction. The scale height is fixed as 0.5m

3.3 표면 돌출부의 기하학적 특성과 하중 방향에 따른 메커니즘 검증

표면 돌출부 기하학적 특성(돌출부 크기와 돌출부 관입 방향)에 따라서 다른 콘 관입 저항을 보였다. 돌출부를 갖는 콘 하중 관입 메커니즘은 콘 돌출부와 주변 요소들 사이에서 국부적으로 발생하는 경계면 전단 저항에 의해서 궁극적으로 결정된다. 이러한 경계면 전단 거동 특성을 정량적으로 분석하기 위해서, 콘 두부에 일정한 하중(=45MN)을 가한 조건에서 표면 돌출부 주변 지반에서의 전단응력을 Contour로 도시하였다.

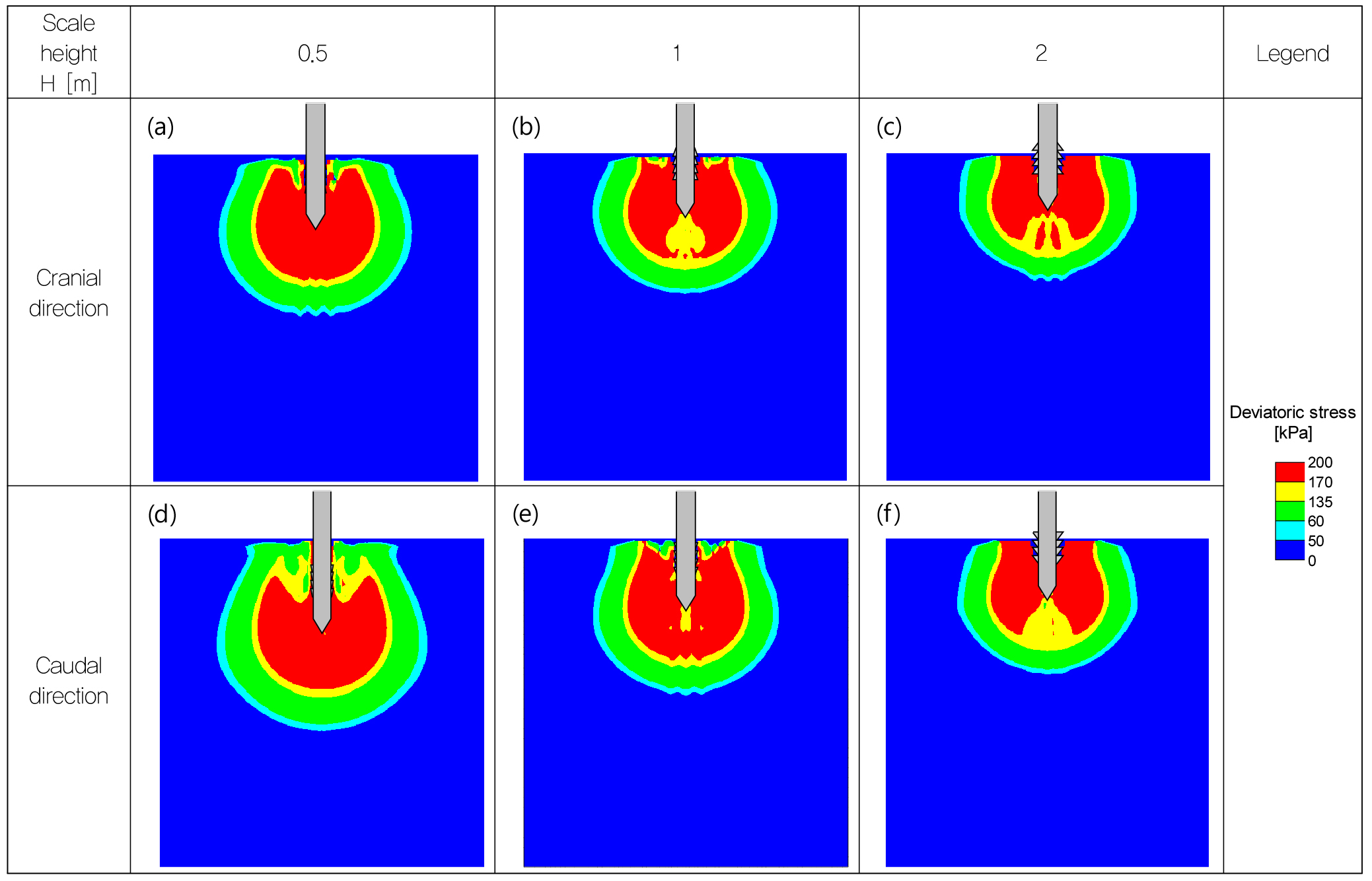
Fig. 6은 선택된 표면 돌출부 높이 H(=0.5m, 1m, 2m)에서 두 가지 하중 방향에 따른 편차 응력(deviatoric stress) 분포를 보여준다. 편차 응력의 증가는 전단 응력의 증가를 의미한다. cranial 하중 방향에서 표면 돌출부 높이가 낮은 경우에는 표면 돌출부 4개를 포함하여 21.3m까지 관입되었으나, 표면 돌출부 높이가 증가함에 따라 콘 관입 깊이는 감소하였다(H = 2m에서 표면 돌출부는 3개만 관입됨). 또한, 돌출부 높이가 H = 0.5m인 경우,표면 돌출부가 존재하더라도 콘 선단 주변에서는 느슨한 모래 지반에서 흔히 발생하는 얕은 기초의 파괴 형상과 유사한 편차 응력 분포를 보였다. 하지만, 돌출부 높이가 증가함에 따라 콘 선단에서의 전단 저항이 감소하였고, 대신 돌출부 주변에서 더 높은 편차 응력이 발생하며, 콘 주면 저항력을 증가시켰다(Fig. 6(a-c)). 또한, 모든 조건에서 caudal 관입 방향이 cranial 관입 방향에 깊은 깊이까지 관입되었으며, 표면 돌출부 높이가 높아질수록 돌출부 높이가 낮은 콘에 비해 약 10m 더 얕은 깊이까지 관입되었다. 마찬가지로, 표면 돌출부 높이가 커질수록 콘 선단에서 편차 응력이 적게 발생하여 전단 저항이 감소하였으며, 표면 돌출부 주변으로 편차 응력이 증가하여 콘 주면 저향력을 증가시켰다(Fig. 6(d-f)).

Fig. 6.

Load transfer around the cone according to the scale height with the load direction. The scale length is fixed as 2.5m. The load on the cone head is constant at 45MN

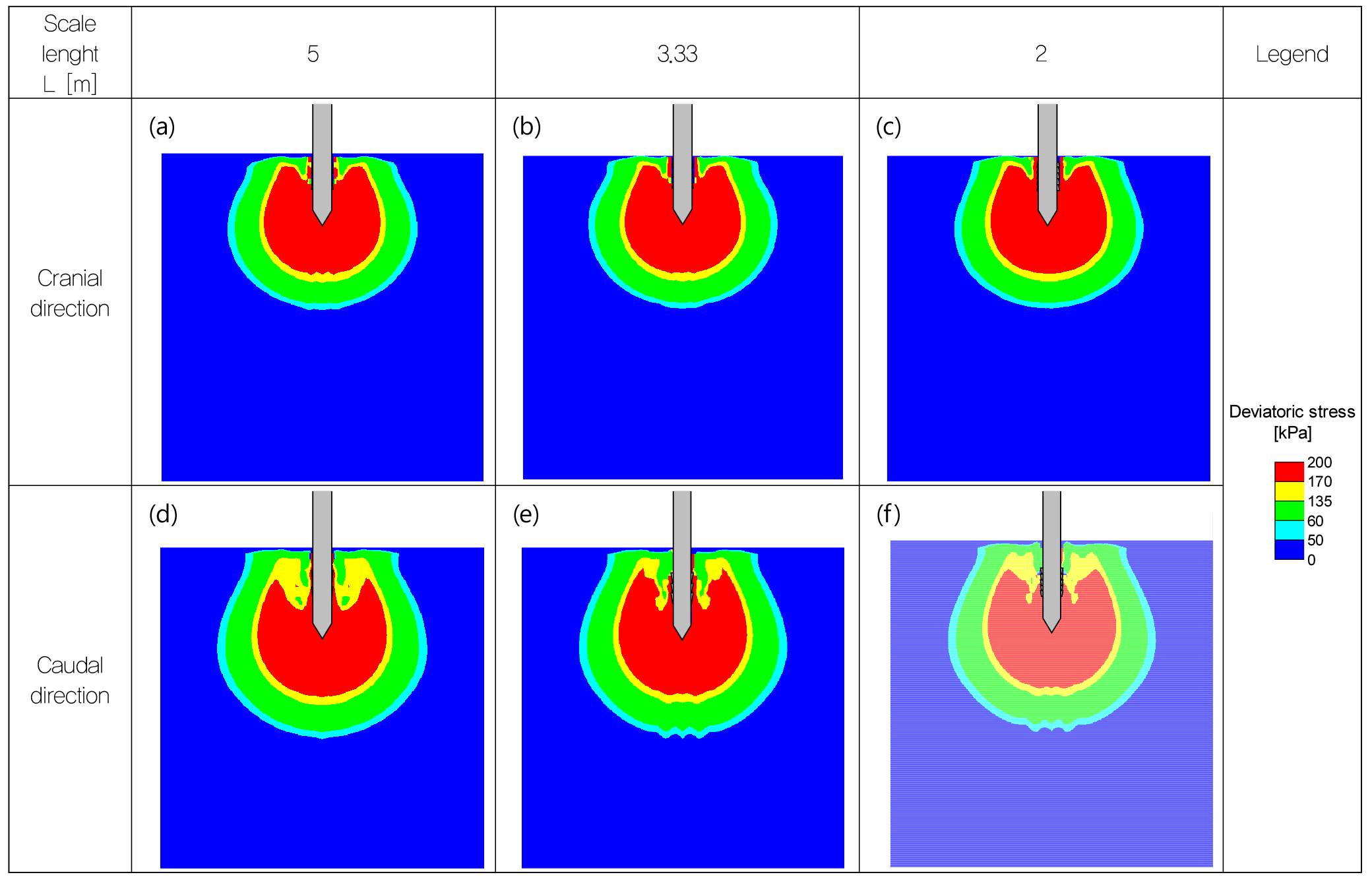
Fig. 7은 선택된 표면 돌출부 길이 L(= 2m, 3.33m, 5m)에 대해 두 가지 하중 방향에 따른 편차 응력 분포를 각각 보여준다. 모든 경우에 cranial 관입 방향이 caudal 관입 방향보다 돌출부 주변에서 높은 편차응력이 발생하였으며, 이로인해 더 높은 관입 저항을 보였다. 하지만, 예상한 바와 같이, 표면 돌출부 길이에 따른 편차 응력 분포의 차이는 거의 미비하였다.

Fig. 7.

Load transfer around the cone according to the scale length with the load direction. The scale height is fixed as 0.5m. The load on the cone head is constant at 45MN

4. 표면 돌출부의 형상비에 따른 정규화된 콘 관입 깊이

본 연구에서 수행된 표면 돌출부의 기하학적 매개변수 해석 결과, 표면 돌출부의 기하학적 조건은 콘 관입 시 주변 지반의 하중 전이에 영향을 주고, 동일한 표면 돌출부 형상에서도 하중 방향에 따라서 다른 하중 전이 특성을 보임을 확인하였다. 돌출부 길이와 높이의 비로 정의되는 표면 돌출부 형상비(scale geometry ratio)와 표면 돌출부를 갖는 콘의 관입 깊이를 표면 돌출부가 없는 콘의 관입 깊이로 정의되는 정규화된 콘 관입 깊이 d_N를 이용하여 Fig. 8과 같이 나타내었다. 관입 깊이는 콘 관입 하중이 45MN에 상응하는 값으로 산정하였다.

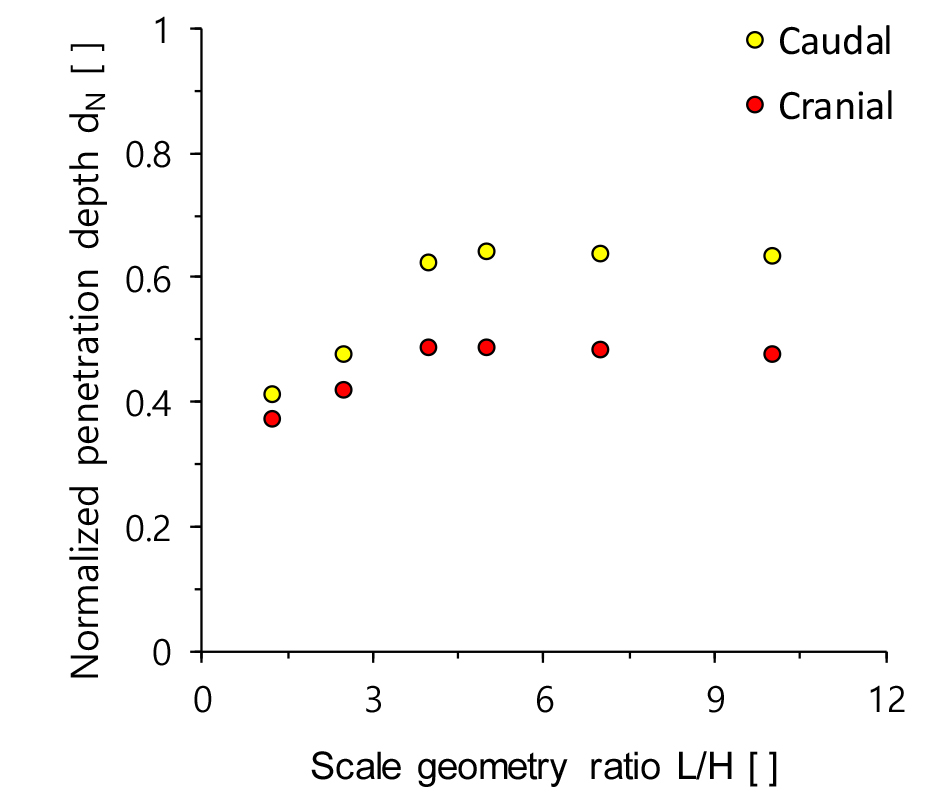
Fig. 8.

Penetration depth according to scale geometry ratio. The normalized penetration depth is calculated by dividing penetration depth of textured cone by penetration depth of smooth cone. Note that a large L/H can be indicated as a lower scale height at the same scale length. The penetration depth value is defined by taking force value at 45MN

모든 표면 돌출부 형상비에서 정규화된 관입 깊이는 1보다 작게 나타났으며, 이는 표면 돌출부가 존재할 경우 관입 깊이가 감소하였을 의미한다. 모든 하중 방향에서 초기 표면 돌출부 형상비에 따라 정규화된 콘 관입 깊이가 급격히 증가하였으나, 특정 표면 돌출부 형상비(= 4)부터 점차 수렴하였다. 돌출부 높이가 증가하는 caudal direction는 돌출부 높이가 감소하는 cranial direction보다 표면 돌출부 형상비에 상관없이 모든 경우에서 더 높은 정규화된 관입 깊이를 보였다. 특히, 표면 돌출부 형상비가 증가함에 따라 하중 방향에 따른 정규화된 콘 관입 깊이 차이는 점차 커지는 경향을 보였다(L/H = 1.25일때 d_N = 0.04, L/H = 5일 때 d_N = 0.13, 그리고 L/H =10에서 d_N = 0.15).

5. 결 론

본 연구에서는 Coupled Eulerian-Lagrangian(CEL) 기법을 활용하여 돌출부 표면을 갖는 콘과 지반 사이의 경계면 전단 거동에 대해 대변형 해석을 수행하였다. 7가지 돌출부 표면 형상과 두 가지 관입 하중 방향을 고려하여 총 13개의 케이스를 해석하였고, 관입된 콘 주변 지반의 하중 전이 메커니즘을 분석하였다. 추가적으로, 돌출부 표면 형상에 따른 경계면 마찰 특성을 정량적으로 분석하여 얻어진 결론은 다음과 같다.

1.대변형 수치해석에서 발생할 수 있는 메쉬의 왜곡과 뒤틀림을 방지하기 위해 Coupled Eulerian-Lagrangian(CEL) 기법을 적용하였으며, 지반 요소 모델링에는 Hex-structured mesh 기능을 이용하여 효율적이고 일관된 메쉬를 생성하였다. 본 연구에서 제안한 정량화된 메쉬는 이론식과 수치해석 결과가 거의 유사하게 나타났으며, 이를 통해 제안된 콘 관입 수치해석 모듈의 신뢰성을 확인하였다.

2.하중 방향(caudal과 cranial)이 콘 관입 저항과 전단 거동에 미치는 영향을 분석하였다. 일정한 돌출부 길이 조건에서 돌출부 높이가 증가할수록 관입 깊이는 얕아졌지만, 일정한 돌출부 높이 조건에서 돌출부 길이에 따른 관입 깊이 차이는 거의 미비하였다. 또한, 모든 경우에서 cranial 관입 방향이 caudal 관입 방향보다 더 얕은 깊이까지 관입되었다.

3.돌출부를 갖는 콘 하중 관입 메커니즘은 콘 돌출부와 주변 요소들 사이에서 국부적으로 발생하는 경계면 전단 저항에 의해서 궁극적으로 결정된다. 돌출부 높이가 증가할수록 콘 관입 깊이는 감소하고, 콘 선단의 전단 저항은 감소하는 반면, 돌출부 주변에서 편차 응력이 증가하며 주면 저항력이 증가한다. 모든 조건에서 caudal 관입 방향이 cranial 관입 방향보다 더 깊은 깊이까지 관입되었으며, 돌출부 높이가 증가할수록 cranial 방향에서 얕은 깊이까지 관입되었다.

4.돌출부 길이는 관입 저항과 편차 응력 분포에 미치는 영향이 미비하였으며, cranial 방향이 caudal 방향보다 돌출부 주변에서 더 높은 편차 응력을 생성하며 더 높은 관입 저항을 보였다. 이러한 결과는 돌출부 높이와 관입 방향이 콘 관입 성능에 주요한 영향을 미치는 반면, 돌출부 길이는 상대적으로 영향이 적음을 보여준다.

5.표면 돌출부 형상비가 증가할수록 정량화된 관입 깊이는 증가하였고, 표면 돌출부 형상비와 관계없이 모든 경우에서 돌출부 높이가 감소하는 cranial direction이 caudal direction보다 더 얕은 깊이까지 관입되었다.

본 연구는 지하수의 영향을 고려하지 않은 유효 응력 해석을 수행하였다. 초기 지하수 존재는 콘 관입 속도에 따라서 콘 주변에서 발생된 초기 과잉 간극 수압 소산 정도가 달라지게 된다. 이로 인해, 콘 주면 주변의 유효 응력 증가량이 달라지므로, 주면 마찰력 증가량도 달라지게 된다. 과잉 간극수의 소산을 전혀 허용하지 않는 콘 관입 속도는 주면 마찰력 증가가 상대적으로 적고, 모든 과잉 간극 수압이 소산될 만큼의 매우 느린 콘 관입은 현재 해석 결과와 마찬가지로 돌출부 표면에 따라서 콘 주면 마찰력의 증가를 야기할 것으로 사료된다. 추후 연구에서는 (a) 지하수 존재와 돌출부 표면의 기하학적 조건에 따른 관입-인발 하중 전이 변화 분석, (b) 실내 실험 결과들에 대한 모델 켈리브리에션과 해석 결과들의 물리적인 검증, 그리고 (c) 최적화된 돌출부 형상을 제안할 예정이다.