1. 서 론
2. 연구 방법
2.1 현장인발시험 개요
2.2 현장시험 준비
2.3 시험방법 및 과정
2.4 이론식과의 비교·분석
3. 현장시험 결과
3.1 최대인발하중
3.2 현장시험 결과
3.3 이론식과의 비교·분석
4. 결 론
1. 서 론
제방은 하천홍수로부터 인근 주거지와 농작지 등 인적·물적 재산을 보호하는 가장 기본적이고 전통적인 하천시설물의 한 종류로서 최근 몇 년간 집중호우로 인한 제방 붕괴로 많은 피해가 발생하고 있다(Ahn et al., 2019). 국내의 경우 1960년 이후 제방축조사업을 본격적으로 시작하였으나, 지방하천과 소하천에 대한 제방축조 및 보수현황은 미비한 실정이다(Kang and Ahn, 2023). 또한 이상기후로 인한 기후변화로 집중호우, 태풍 등에 따른 제방 붕괴 및 홍수에 대한 잠재적 위험성이 점증하고 있다(Kang and Woo, 2021).
이와 같은 이상기후 및 홍수에 대비하기 위해 여러 기술들이 개발되고 있으며, 90년대 이후부터는 기존의 콘크리트 구조물 및 블록을 대체하기 위한 경제적이고 친환경적인 스톤 네트 보강재의 사용이 증가하고 있다(Lee et al., 2022). 스톤 네트 공법은 자연석과 철망이 일체화되어 소류력에 저항하는 자연친화적 공법으로 이러한 공법은 하천과의 고정 효과를 위해 여러 고정장치를 활용함으로써 안정성을 향상하고 있으나, 고정장치의 안정성 및 적용에 대한 연구가 미흡하고 적용 기준 또한 마련되지 못한 실정이다(Kim, 2011). 스톤네트가 제대로 고정되지 못한 경우 지반과의 마찰력 저하로 인한 제방의 슬라이딩 현상 등이 발생해 비탈면 붕괴가 발생하는 등 여러 문제가 발생할 수 있다. 이에 따라 스톤네트를 하천에 제대로 고정시키고 집중호우 시 스톤네트의 유실 및 파손을 막기 위해 하상에 지반고정형 앵커핀을 근입 후 앵커핀과 스톤네트를 연결하는 보강방안을 적용함으로써 치수적 안정성을 확보하기 위한 기술이 개발되고 있다.
본 연구에서는 하천제방 보강에 많이 사용되고 있는 스톤네트용 플레이트 앵커핀을 대상으로하여, 총 7개의 단면형상에 대한 현장인발시험을 수행하고 기존 이론식과의 비교·검토를 통해 단면 형상별 앵커핀 인발에 따른 최대인발하중과 지반 변위 영향범위를 고찰하였다. 본 연구를 통해 향후 하천방재시설물의 설계 기술 및 성능 향상에 기여할 수 있는 기초 자료를 제공할 수 있을 것으로 판단된다.
2. 연구 방법
2.1 현장인발시험 개요
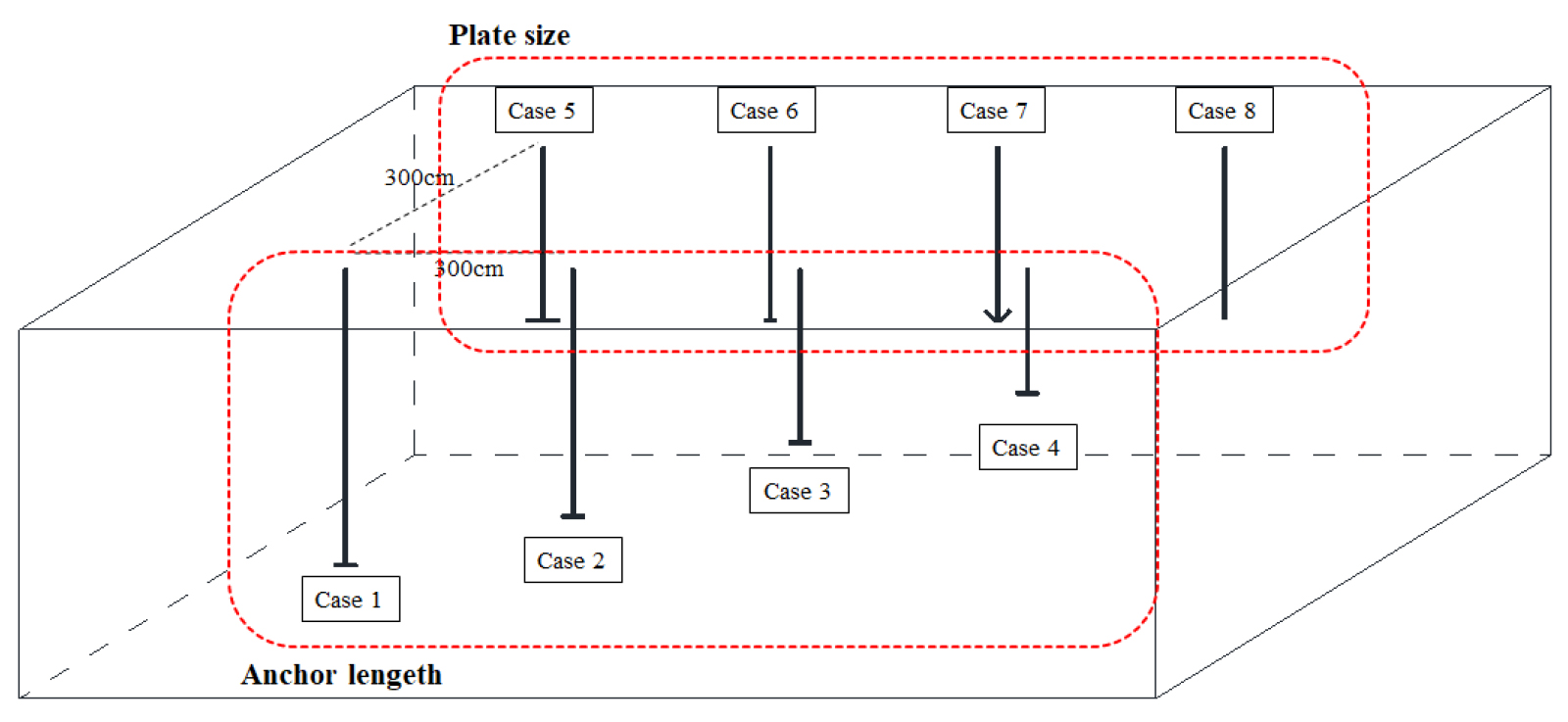
본 연구에서는 하천제방 보강에 주로 사용되는 스톤네트용 플레이트 앵거핀의 인발과정에서의 거동을 분석하기 위해 현장시험을 수행하였다. 현장시험은 Fig. 1과 같이 경기도 가평에 위치한 하천제방 보강공사 현장에서 수행하였으며, 인발저항특성과 지반 변형 거동을 분석하기 위해 Table 1과 같이 조건을 상정하였다.
Table 1.
Conditions of pull-out tests
| Type | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | Case 7 | Case 8 |
| Length (H, cm) | 120 | 100 | 70 | 50 | 70 | 70 | 70 | 70 |
| Plate Size (h, cm) | 10 | 10 | 10 | 10 | 15 | 5 | 10(V) | - |
시험 조건은 앵커핀 길이에 따른 거동특성 분석을 위해 플레이트의 크기를 10cm로 고정하고 앵커핀의 길이를 Case 1 ~ Case 4와 같이 적용하였으며, 플레이트 크기에 따른 거동 특성을 분석하기 위해 앵커핀의 크기를 70cm로 고정하고 플레이트의 크기 및 형상을 평면형인 경우(Case 5, Case 6)와 V형인 경우(Case 7), 플레이트 미적용 일자형 앵커핀(Case 8)으로 변화시키며 거동 특성을 분석하였다. 이때 선택한 플레이트 크기 10cm 및 앵커핀 길이 70cm는 기존 일자형 앵커핀을 대체하기 위해 현장에서 주로 사용되는 앵커핀의 표준 사양 중 하나이다.
현장인발시험은 하중제어 방식을 통해 수행하였으며, 하중을 선형적으로 증가시켜 목표 하중에 도달한 후 이를 유지하는 단순재하방식을 선택하였다. 재하 하중은 관련 이론식(Downs and Chieurzzi, 1966)을 통해 계산된 극한인발하중에 근접한 2000kgf를 적용하였다. 또한 현장시험을 위한 앵커핀의 배치간격은 Fig. 2와 같이 앵커의 그룹효과를 고려한 3m로 적용하였다.
2.2 현장시험 준비
2.2.1 플레이트 앵커핀 제작
본 연구에서 활용한 플레이트 앵커핀은 크롬 18%와 니켈 8%를 함유하여 내부식성이 우수한 스테인리스강 304(Stainless steel 304)를 활용하여 제작하였다.
앵커핀과 플레이트의 조립은 용접방식 대신 T형 캡볼트와 6각 너트를 사용하여 체결하였으며, Case별 조건에 따라 앵커핀의 길이 및 플레이트의 폭을 Fig. 3과 같이 다르게 적용하여 제작하였다.
2.2.2 현장지반조건
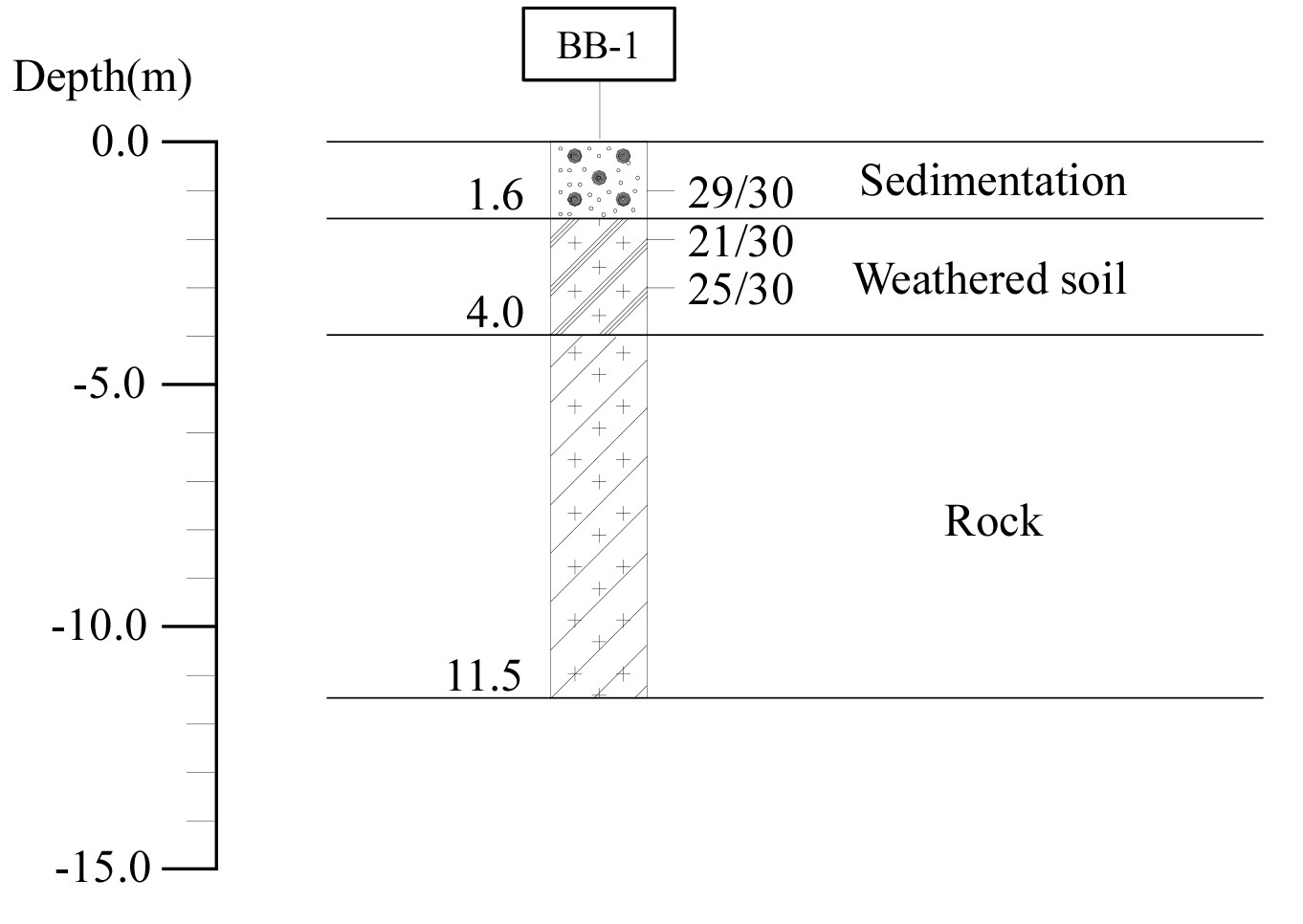
현장시험을 수행할 지반을 대상으로 시추조사, 표준관입시험, 입도시험, 들밀도시험 등 현장조사를 통해 얻은 지반 현황은 Fig. 4와 같으며, 물성은 Table 2와 같다.
Table 2.
Material properties of the soil
| G | wn(%) |
Cohesion c (kgf/cm2) |
Friction angle (°) |
Atterberg limit (%) | Grain size distribution (%) | USCS | |||||
| LL | PI | #4 | #10 | #40 | #200 | 0.005mm | |||||
| 2.668 | 10 | 4 | 30 | 30.5 | 12.2 | 72.6 | 62.9 | 47.5 | 35.4 | 15.6 | SC |
2.3 시험방법 및 과정
현장인발시험은 Fig. 5와 같이 현장을 가로 10m, 세로 20m 규모로 평탄화 후 3m 거리를 이격하여 목표설치 심도까지 앵커핀을 매설하였다.
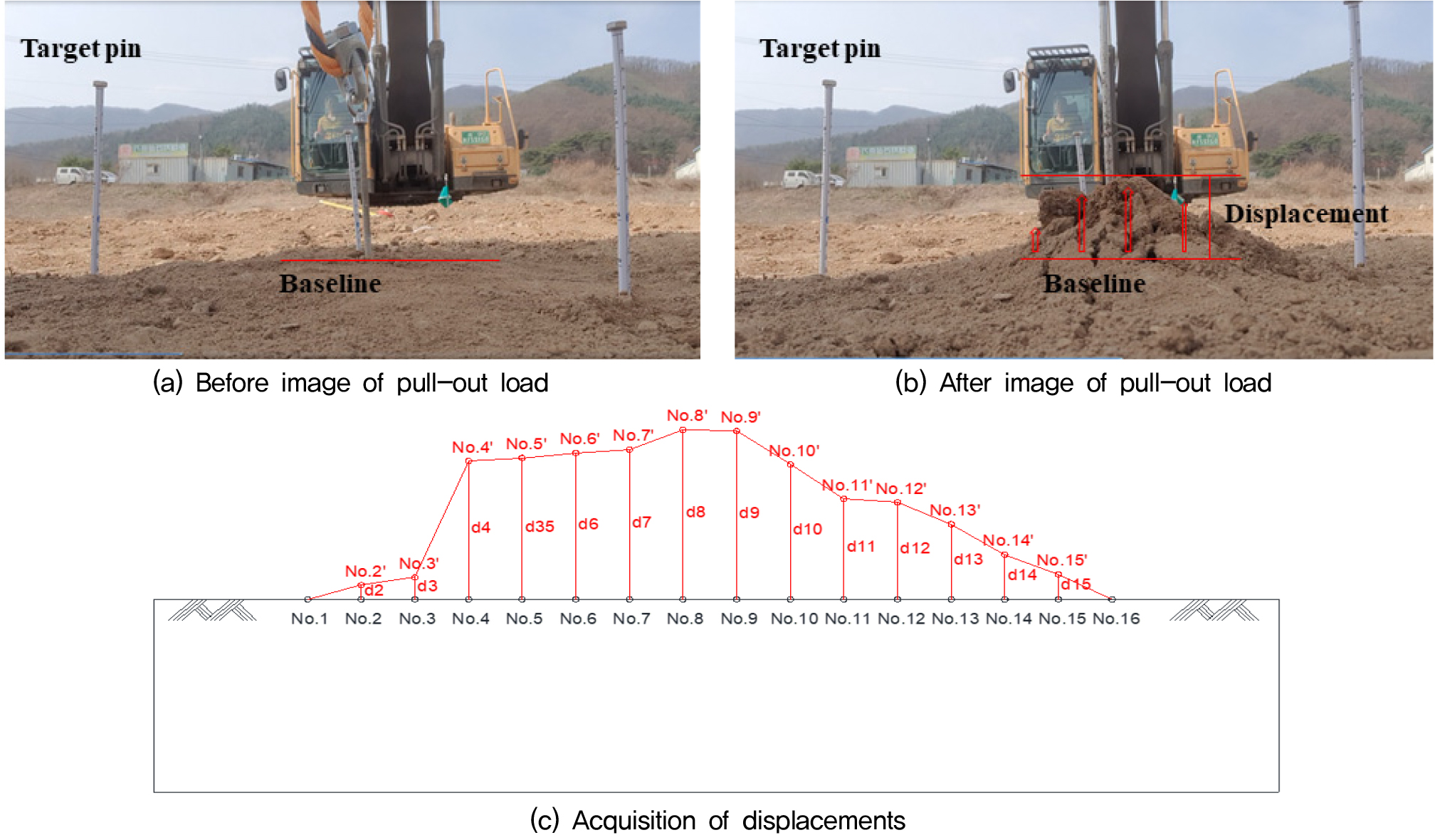
앵커핀 매설 후 반경 20cm의 원에 내접하는 3점을 표시하여 지반변형분석을 위한 기준점을 설치하였다. Fig. 6과 같이 앵커핀 주위에 설치한 기준점을 촬영하기 위한 Digital camera를 설치하였으며, 실험 전후의 사진을 촬영하여 영상 분석을 통한 지반 변위 분석을 수행하였다.
인발하중은 시험시작과 동시에 백호우를 통해 지반의 연직방향으로 33.3kg/sec의 속도로 앵커핀을 인발하도록 설정하고, 2,000kgf에 도달 후 추가적인 하중 증가없이 유지하는 것으로 계획하였다.
2.4 이론식과의 비교·분석
본 연구에서는 대표적 이론식 중 하나인 Meyerhof and Adams(1968) 이론식 및 Saeedy(1987) 이론식, Downs and Chieurzzi(1966) 이론식을 통해 산정한 값을 현장시험을 통해 얻어진 결과 값과 비교·분석하였다. Meyerhof and Adams(1968) 이론식의 경우 앵커가 인발될 경우의 파괴면을 곡선형태로 가정하여 인발력을 산정하였으며, 인발력은 식 (1)과 같다.
여기서, : 극한인발력
: 앵커 위 흙의 무게
: 앵커의 매입 깊이
: 흙의 단위중량
: 공칭인발계수
: 흙의 내부 마찰각
Saeedy(1987) 이론식의 경우 극한 인발력에서 파괴 거동은 대수의 나선형 원호로 추정된다고 주장하였으며, 식 (2)와 같이 계산된다.
여기서, : 극한인발력
: 파괴계수
: 앵커의 매입 깊이
: 흙의 단위중량
: 앵커판의 면적
: 압축요소
Downs and Chieurzzi(1966) 이론식의 경우 원뿔 형태의 흙의 부피를 사용하고 있으나, 본 연구에서는 사각형 플레이트를 활용하였으므로 사다리꼴 형태의 흙의 부피를 고려할 수 있도록 이론식을 식 (3)과 같이 수정하였다. 여기서 는 지표면과의 파괴각으로 60°로 적용하였다.
여기서, : 극한인발력
: 흙의 단위중량
: 흙의 부피
: 파괴면의 각
: 지압형 앵커가 지반에 묻힌 깊이
: 지압형 앵커의 길이
: 지압형 앵커의 폭
3. 현장시험 결과
3.1 최대인발하중
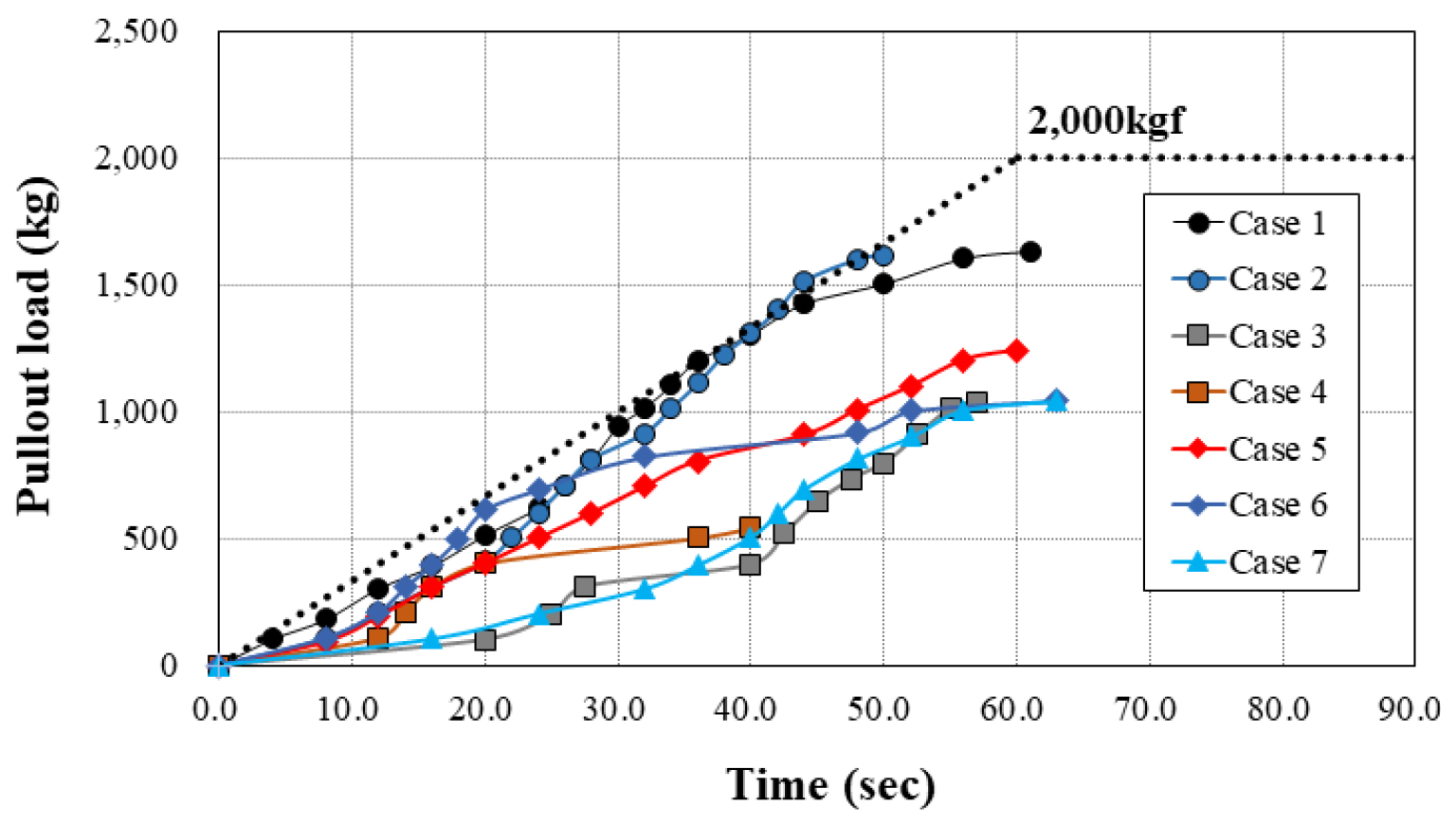
현장인발시험 결과, 플레이트가 없는 경우인 Case 8의 경우는 하중 증가와 동시에 앵커핀이 인발되어 유의미한 결과를 얻기 어려운 것으로 판단되어 분석대상에서 제외하였다. Case 8을 제외한 나머지 Case에 대한 인발하중과 최대인발 하중 도달 시간에 대한 시험결과는 Table 3과 Fig. 7과 같다.
Table 3.
Results of pull-out load
모든 Case에서 인발하중 부가후 시간경과에 따라 인발하중이 증가하였으며, 목표하중 2,000kgf에 도달하기 전에 최대 인발하중을 나타내었다.
최대 인발하중의 크기는 Case 1에서 1,634kgf에서 가장 큰 값을 나타내었으며 Case 4에서 543kgf로 가장 작은 값을 나타내었다. 분석 결과 앵커핀의 길이가 길수록, 플레이트의 면적이 넓을수록 증가하였는데 이는 플레이트 상부 토사의 자중이 저항력으로 작용한 것으로 판단된다.
Case 1과 Case 2의 경우 최대 인발하중에 큰 차이가 없는 것으로 나타났는데 이는 최대 인발하중에 도달 후 플레이트판이 Fig. 8과 같이 파손됨에 따라 하중에 저항하지 못한 것으로 판단된다.
3.2 현장시험 결과
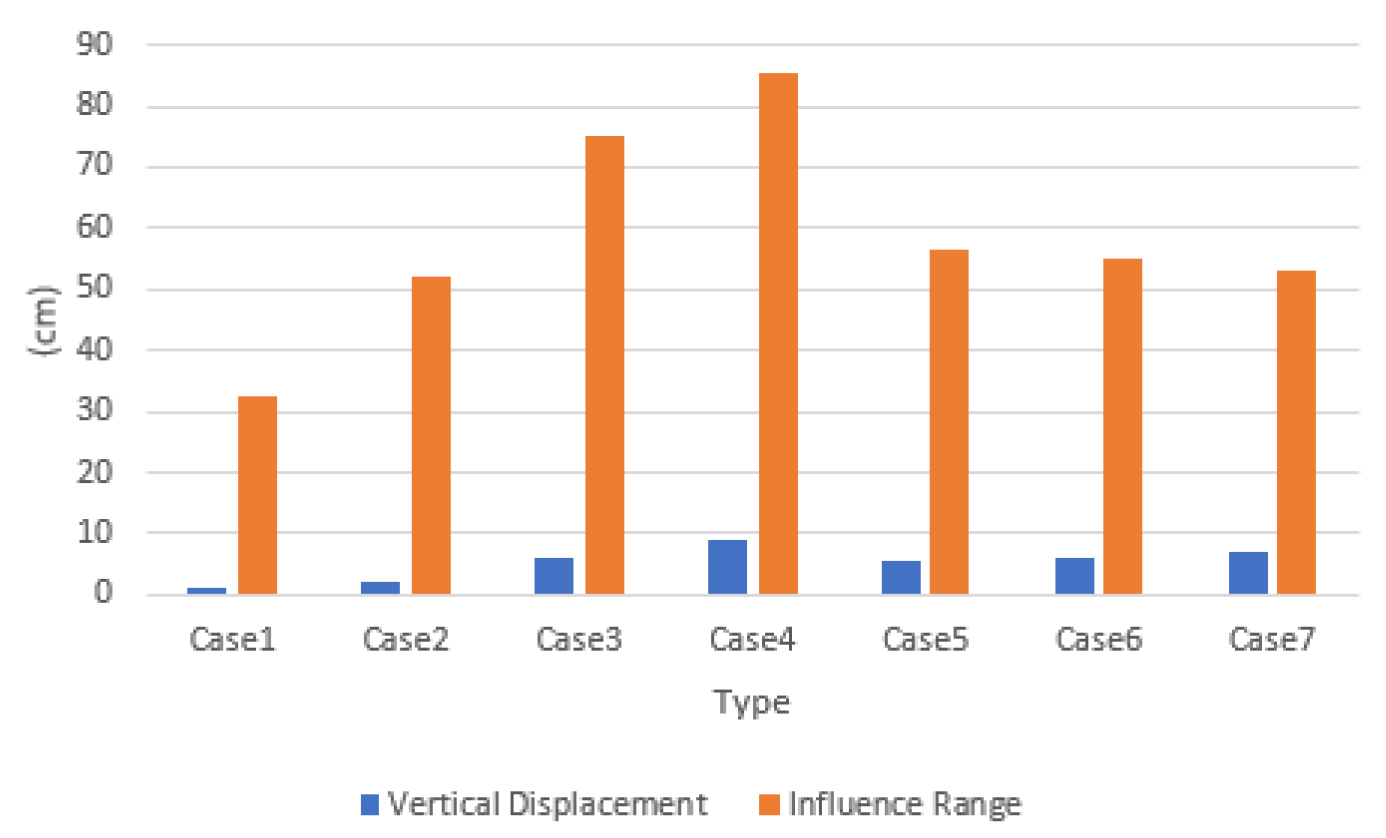
현장인발시험 변형 전과 변형 후의 x, y좌표를 확인하였으며, 기준선을 비교하며 변형 전후의 지반 변형을 확인하였다. Fig. 9는 현장인발시험 및 변형 결과를 나타내며 각 지점의 번호는 실험 전 후의 화상을 측점을 기준으로 Autocad를 사용해 도면화한 지점이다. Target pin간의 거리는 34.5cm이고, No.간의 거리는 2.3cm이다. Case 별 최대 지반변위 및 영향범위는 Table 4 및 Fig. 10과 같다.
앵커핀의 길이가 짧은 경우 앵커핀 주변에서 형성된 파괴면이 지표면에 영향을 미치는 것으로 판단되며, 앵커핀의 길이가 긴 경우 파괴면이 지표면에 미치는 영향은 적은 것으로 판단된다.
최대 인발하중이 큰 Case 1 및 Case 2에서 가장 적은 변위가 발생했으며, 최대 인발하중이 가장 작은 Case 4에서의 변위가 가장 크게 나타났는데 이는 앵커핀에 인발하중이 작용한 경우 플레이트 상부 토사의 자중이 저항력으로 작용하며 지반의 거동을 억제하였기 때문인 것으로 사료된다.
Case 별 앵커핀이 파괴될 경우 지반 영향범위는 인발시험 종료 후 지반이 변형된 형상을 줄자를 통해 확인하였다.
모든 Case에서의 영향범위는 지반변형의 경향과 일치하며, 이는 앵커핀 인발과 동시에 지반의 압축이 발생하며 변형이 시작되기 때문인 것으로 판단된다.
Table 4.
Results of displacement
3.3 이론식과의 비교·분석
기존 이론식을 통해 산정한 인발저항력과 현장시험을 통해 얻은 결과 값을 비교·분석한 결과는 Table 5와 같다.
분석 결과 Meyhof and Adams 이론식의 경우 앵커핀의 설치심도 증가에 따라 극한인발하중값이 급격하게 증가하였다. 모든 Case에서 이론식을 통해 산정한 극한인발력은 현장시험 결과 값보다 설치심도(H)의 경우 191kgf ~ 613kgf 정도 작은 값을 나타내었으며, 플레이트 면적(h)의 경우 543kgf ~ 728kgf 정도 작은 값을 나타내었다.
Saeedy에 의해 산정한 극한인발하중값의 경우 다른 이론식에 비하여 상당히 작은 값을 나타내었는데, 이는 지반의 내부마찰각이 다소 작게 산정되었기 때문으로 판단되며, Saeedy 이론식의 경우 내부마찰각이 35° 이상인 조밀한 지반에서 적용하는 것이 타당할 것으로 판단된다.
Down and Chieurzzi 이론식의 경우 Meyerhof and Adams 이론식에서 산정한 값과 변화 경향이 유사하나 설치심도에 따른 편차가 더 심하게 나타났다. Case 1을 제외한 모든 Case에서 이론식을 통해 산정한 값은 현장 시험보다 작은 값을 나타냈으며, 설치심도에 대해 297kgf ~ 599kgf 정도, 플레이트 면적에 대해서는 629kgf ~ 751kgf 정도의 차이가 발생하였다.
Table 5.
Comparison of theories and tests
4. 결 론
본 연구에서는 하천제방 보강에 주로 사용되는 스톤네트용 플레이트 앵커핀을 대상으로 총 7개의 Case 별 현장인발시험을 통해 앵커핀 인발에 따른 최대인발하중과 지반변위 및 영향범위를 분석하였으며, 기존 이론식과의 비교·분석을 통해 앵커핀의 인발에 따른 거동을 고찰하였다. 본 연구를 통해 얻어진 결론은 다음과 같다.
1.총 7개 Case에 대한 현장인발시험 결과, 최대인발하중의 크기는 앵커핀의 길이가 길수록, 플레이트 판의 면적이 넓을수록 증가하였다. 변위의 절대 값은 앵커핀의 길이가 100cm 이상인 경우 작게 나타났으며 앵커핀의 길이가 가장 짧은 Case 4에서 변위의 절대 값이 가장 크게 나타났다. 이는 플레이트 상부에 위치한 토사의 자중이 저항인자로 작용했기 때문으로 앵커핀의 길이 및 플레이트 판의 면적과 최대인발하중은 비례하며, 변위의 절대 값은 반비례 관계에 있는 것으로 판단된다.
2.앵커핀 인발에 따른 영향범위 분석 결과 모든 Case에서 앵커핀의 길이 및 플레이트 판의 면적에 따른 영향범위는 지반변형의 경향과 유사하였으며, 이는 앵커핀 인발과 동시에 지반이 상방향으로 압축되며 지반의 변형이 시작되기 때문인 것으로 판단된다.
3.설치심도 100cm 이상인 Case 1과 Case 2를 제외한 현장시험 결과와 이론식을 통해 산정된 값을 비교 분석한 결과, Saeedy 이론식은 시험 값과 큰 차이를 나타냈으나, Meyerhof and Adams 이론식은 시험 값의 41%에서 49%의 정도, Down and Chieuizzi 이론식은 39%에서 45% 정도로 나타나 두 이론식은 비슷한 경향성을 보이는 것으로 판단된다.
향후 지속적인 연구를 통해 다양한 지반조건에서의 현장 시험 검토 및 수치해석을 통한 검토를 통하여 하천보강 스톤네트용 플레이트 앵커핀의 최적 단면 산정 및 영향반경에 대한 예측기법의 정립이 필요하며, 본 연구를 통해 향후 관련 설계 기술의 향상과 하천방재시설물의 성능 향상을 위한 기초 자료로 제공될 수 있을 것으로 기대된다.