1. 서 론

일반적으로 흙막이 설계는 탄소성보법, 유한요소법 등 수치해석 방법을 통해 수행되며 이때 과업구간에서 수행된 지반조사 결과로부터 구한 설계지반정수를 적용함이 일반적이다. 그러나 설계 시 적용된 지반정수는 과업구간내의 국한된 지점을 대상으로 한 값이므로 해당 과업구간에 설치되는 모든 벽체에 대한 안정성이 평가되었다고 판단하기에는 한계가 있다. 이는 Do et al.(2010)과 Kim et al.(2004)의 연구에서 알 수 있듯이 흙막이 설계가 진행되었음에도 불구하고 현장에서 보고되는 벽체의 추가 변형 및 붕괴사례가 설계의 한계를 반증해주는 것이라 할 수 있다. 또한 벽체설계시의 해석결과와 현장의 계측결과 오차는 지반조건 외 벽체구조의 복잡성과 가변성에 의한 것이라고 보고된 바 있다(Kwon et al., 1999).

최근 이와 같은 문제점을 해결하기 위한 일환으로 시공 중 가시설 구조물의 계측된 결과를 적용하여 최종단계 벽체거동을 예측할 수 있는 역해석 기법에 대한 연구와 이와 관련한 프로그램의 개발이 진행되어 왔다(Akutagawa et al., 1991; Gioda and Jurina, 1981; Gioda and Sakurai, 1987; Chang et al., 2003). 역해석 프로그램은 조정된 설계지반정수를 적용한 역해석 알고리즘을 이용하므로 벽체의 계측결과와 유사한 예측결과를 구할 수 있는 것이 장점이라 할 수 있다(Jang and Kim, 2002; Lee et al., 2006; Kim and Lee, 2013; Park, 2014; Yun, 2019).

역해석 프로그램에 적용되는 기법은 크게 직접알고리즘(Direct Algorithm), 순차적 근사최적화법(Sequential Approximate Optimization), 순차 2차계획법(Sequential Quadratic Programming) 및 유전알고리즘(Micro-Genetic Algorithm)기법 등을 들 수 있다(Gioda and Sakurai, 1987; An et al., 2016). 이들 방법 중 유전 알고리즘은 확률론적 방법이므로 종래의 방법에 비하여 계산종료 조건을 정하기가 어렵고 설계변수의 전 공간에 대한 무작위 탐색의 성격을 어느 정도 가지므로 계산 시간이 길어지는 단점이 있다(Jang, 2002). 또한 직접법은 수학적 방법에 의한 최적화가 여러개의 해가 있을 경우 전체의 최적해가 아닌 국부적인 해를 찾는 문제와 역해석 결과가 초기 설계변수에 따라 달라진다는 문제가 있다(Oh, 2001). 이와 같은 기법의 문제점은 역해석 결과의 적정성에도 영향을 미치므로 최근 들어 이를 극복하기 위한 연구와 지속적인 개발이 진행되고 있다.

본 연구에서는 역해석 기법 및 프로그램의 적용성을 평가하기 위해 직접알고리즘을 적용한 최근 개선된 MIDAS GeoXD의 On Site 프로그램 기능을 이용하여 실제 흙막이 벽체를 대상으로 역해석을 수행하였다. 그리고 직접 알고리즘을 활용한 역해석 결과와 유전 알고리즘을 활용한 역해석 결과 및 현장계측결과를 종합적으로 비교, 분석하여 역해석 기법의 적정성에 대한 최적화 성능을 평가하였다. 또한 굴착단계별로 계측 데이터를 달리 입력한 후 역해석을 수행하고 굴착단계별 역해석 결과(변위 및 부재력)의 적정성을 검토하였다. 그리고 이를 통해 직접알고리즘 역해석 프로그램의 효과적인 활용방안을 제안했다.

2. 흙막이 가시설 역해석 알고리즘

2.1 직접알고리즘

직접알고리즘은 립시츠 최적화(Lipschitz optimization)를 바탕으로 하며, 해석데이터와 계측데이터로 구성된 목적함수의 전역 최적화에 대한 문제 해결이 가능하다. 직접알고리즘의 기본개념은 식 (1)과 같으며 이것을 상수 α에 대한 립시츠 연속성이라 표현하고 xopt∈Ω는 식 (2)를 통해 산정할 수 있다. 직접알 고리즘은 목적함수에 대한 미분이 요구되지 않으며 해의 집단 영역에서 일부를 추출하여 얻은 정보를 사용하여 다음 단계의 해석을 진행한다(Finkel, 2003). 해석은 최적해가 결정될 때까지 해의 집단에 대한 연산을 반복한다.

여기서, ε은 양의 상수이다.

2.2 유전알고리즘

유전알고리즘은 확률론적인 방법을 이용하여 전역적인 해를 찾는 방법으로써 Holland(1975)에 의해 제안되었다. 유전알고리즘의 표준모델은 초기집단구성, 적합도 평가, 재생산, 교배, 돌연변이의 기본 구조를 갖는다(Kim et al., 2003). 이 방법은 초기에 구성된 확률적인 해 집단으로부터 식 (3)과 같이 목적함수[F(x))]의 적합도 평가를 통해 각 해에 대한 우열을 결정하고 재생산을 통해 적합도[f(s))가 높은 해들을 산출한다. 연산된 해의 집단은 최적해가 결정될 때까지 위의 과정을 반복한다.

여기서, r은 f(s)≥0을 만족하도록 하는 상수이다.

3. 흙막이 현장조건 및 계측 결과

3.1 지반 및 가시설 조건

역해석 기법 및 프로그램에 대한 적정성을 평가하기 위해 본 연구에서 적용한 지반조건 및 가시설 단면도는 Table 1 및 Fig. 1과 같다. Fig. 1은 본 연구에서 비교대상으로 검토한 A 현장 및 B 현장의 가시설 구조물의 개요도를 보인 것이다. A 현장의 가시설 벽체는 심도 26.63m의 지반굴착을 위해 설치되었고 총 버팀 단계는 10단 버팀으로 계획되었다. B 현장의 가시설 벽체는 심도 22.90m의 지반굴착을 위해 설치되었고 총 버팀 단계는 7단 버팀으로 계획되었다. 각 현장별 가시설 벽체에 대한 세부 사항은 Table 2와 같다. 또한 굴착 깊이(H)를 고려한 허용 벽체변위(δa=0.002H)는 A현장의 경우 53.26mm, B현장의 경우 45.80mm이다.

Fig. 1.

Section of the retaining wall and ground conditions

3.2 흙막이 계측결과

Fig. 2는 A 및 B현장의 현장계측을 통해 조사된 굴착단계별 발생된 수평변위(δm)를 나타낸 것이다. 계측결과, 지반굴착이 진행됨에 따라 가시설 벽체의 변위는 증가하며 A현장의 경우는 굴착하부 풍화토층의 벽체변위가 가장 크게 발생하였고 이때 최대 변위는 16.90mm인 것으로 조사되었다. B현장의 경우는 매립층과 붕적층의 벽체변위가 굴착 하부 풍화토층의 변위보다 상대적으로 크게 발생되었고 이때 최대 변위는 6.33mm인 것으로 조사되었다. 또한 조사된 A와 B현장의 벽체변위는 설계시 적용한 허용 기준치 이내인 것으로 나타났다.

각 현장은 유사한 가시설 조건을 가지고 있으나 지층구조와 지하수위, 굴착깊이, 시공단계, 버팀간격 등이 상이함에 따라 흙막이 거동이 달라짐을 알 수 있다. 따라서 상이한 각 현장의 흙막이 거동에 따른 역해석 기법의 적정성 평가가 가능할 것으로 보인다.

Fig. 2.

Displacement of earth retaining wall by excavation step through field measurement

4. 역해석 알고리즘 기법에 대한 비교 평가

4.1 역해석 조건

Kang et al.(2023)에 의하면 직접법인 순차 근사 최적화법과 순차 2차 계획법의 경우 시공 초기단계에서는 유전알고리즘 및 직접알고리즘의 역해석 결과와 유사하나 굴착단계가 증가할수록 역해석 결과의 오차가 증가한다고 하였다. 따라서 본 절에서는 비교적 적은 오차를 보이는 직접알고리즘 및 유전알고리즘을 MIDAS GeoXD 프로그램에 각각 적용하여 A 현장과 B 현장에 대하여 역해석을 실시하여 상호 비교하였다. 이때 역해석 케이스는 단조로운 지반조건(매립층, 붕적층)과 비교적 복잡한 지반조건(매립층, 붕적층, 풍화토)에 대한 계측데이터(입력데이터)와 역해석 결과(출력데이터)의 오차를 비교하기 위해 Fig. 3과 같이 굴착깊이를 상이하게 하여 입력데이터를 결정하였다. 이에 A 현장은 4단계 및 8단계 굴착시, B 현장은 3단계 및 7단계 굴착시의 계측데이터와 역해석 결과를 비교하였으며 2개의 역해석 알고리즘에 대한 역해석 조건은 Fig. 3과 같다.

Fig. 3.

Back analysis case for application evaluation of the direct algorithm

4.2 평가결과

2개의 역해석 알고리즘을 이용하여 A현장 및 B현장에 대하여 각 굴착단계의 역해석 변위(δb)와 계측 변위(δm)를 비교한 결과는 Fig. 4와 같이 거의 유사한 경향을 보이는 것으로 나타났다. 또한 직접알고리즘과 유전알고리즘을 비교한 결과는 서로 유사한 경향을 보였으나 Fig. 4(b), (d)와 같이 굴착심도가 깊어질수록 계측 결과와의 유사성은 직접알고리즘이 비교적 높은 것으로 확인되었다. 따라서 직접알고리즘과 유전알고리즘은 모두 흙막이 역해석에 대한 적용성이 뛰어난 것으로 판단되나 본 프로그램을 통한 상호 비교에서는 직접알고리즘이 유전알고리즘보다 계측데이터에 대한 최적화가 약간 더 우수한 것으로 평가되었다.

Fig. 4.

Comparison between measurement results and back analysis results

5. 직접알고리즘 역해석 기법을 통한 굴착단계별 적용성 평가

5.1 역해석 조건

4.2절에서 역해석 기법인 유전자알고리즘과 직접알고리즘에 대하여 초기굴착 단계와 후반부 굴착단계에 대하여 수평변위를 비교한 결과 직접알고리즘이 유전자 알고리즘에 비해 다소 그 적용성이 우수한 것으로 평가되었다. 따라서 본 절에서는 직접알고리즘만을 대상으로 프로그램을 통해 굴착단계별 계측데이터에 따른 역해석 결과에 대한 적용성을 평가하였다. 이를 위해 먼저 Fig. 5와 같이 각 굴착단계별 계측 데이터(A현장은 1, 3, 5, 7, 9단계; B현장은 1, 3, 5, 7단계)를 입력하여 역해석을 실시하였으며 이때 각 현장의 풍화토층은 대체적으로 조밀하게 형성되어 있다는 점과 설계의 단순화를 고려하여 단일지층으로 모델링하였다. 다음으로 역해석 결과(δb, Pb)와 계측결과(δm, Pm)는 굴착깊이가 깊어짐에 따라 가시설 안정성에 문제가 발생할 수 있는 굴착공사 후반 단계(A현장은 8, 9, 10, 11단계; B현장은 5, 6, 7, 8단계)를 중심으로 상호 비교 검토하였다. 그리고 마지막으로 굴착 후반단계에 대한 역해석 결과는 계측 결과와의 오차를 산정하여 상호 비교 분석하였다.

Fig. 5.

Back analysis case according to the measurement data by excavation step

5.2 역해석 변위 결과

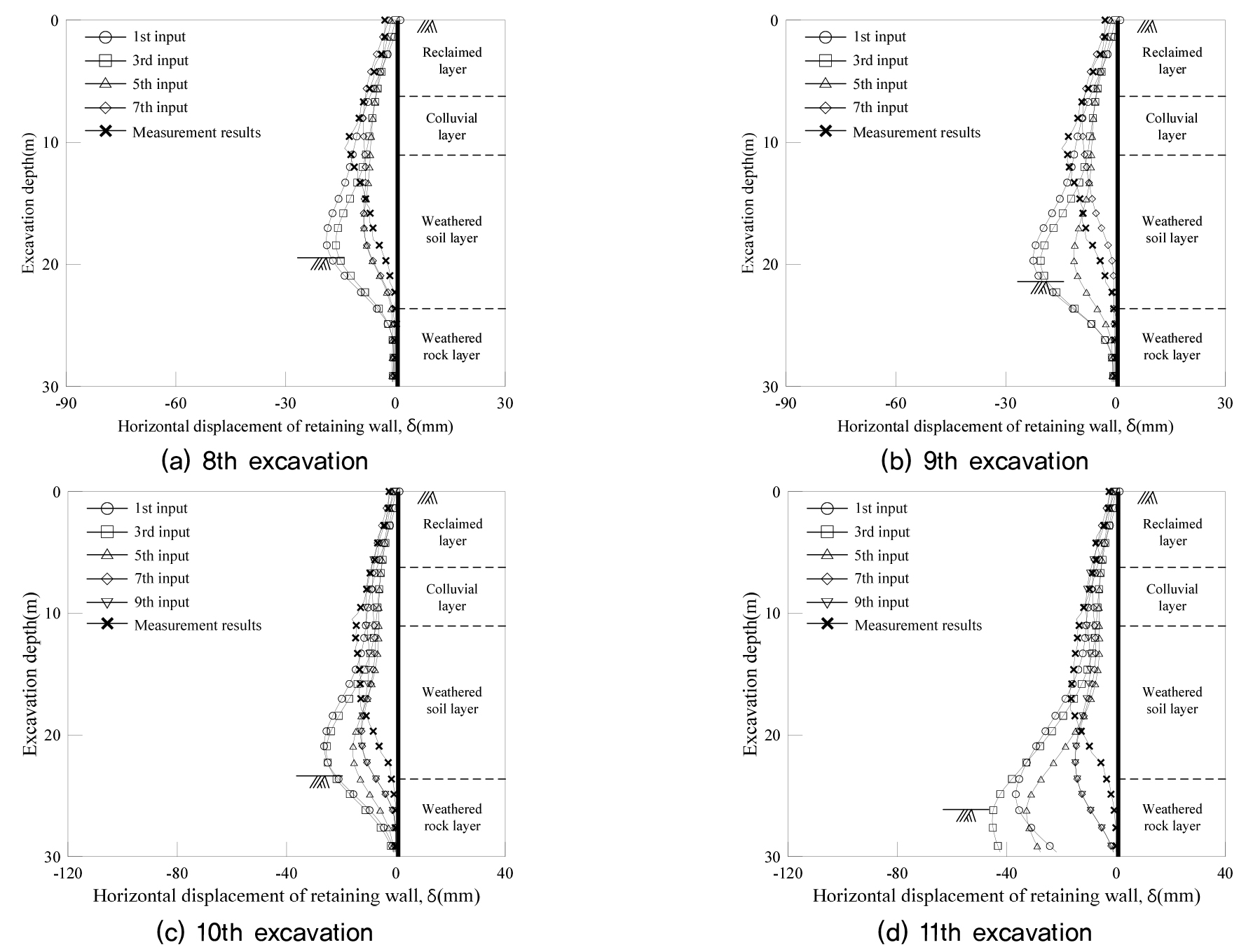
굴착단계별 역해석 결과(δb)와 계측결과(δm)의 흙막이 변위는 Fig. 6∼7과 같다. A 현장에 대한 역해석 결과는 굴착 최종단계인 11단계(Fig. 6(d)) 굴착시의 흙막이 최대변위는 계측결과의 경우 16.90mm, 역해석 결과의 경우 입력된 계측데이터에 따라 14.86mm∼45.25mm 만큼 발생하였다. B 현장에 대한 역해석 결과는 굴착 최종단계인 8단계(Fig. 7(d)) 굴착시의 흙막이 최대변위는 계측결과의 경우 6.33mm, 역해석 결과의 경우 입력된 계측데이터에 따라 6.83mm∼21.74mm 만큼 발생하였다.

Fig. 6.

Comparison of earth retaining wall displacement at field A

Fig. 7.

Comparison of earth retaining wall displacement at field B

A현장과 B현장은 모두 굴착심도가 깊어짐에 따라 벽체 하부구간에서의 역해석 결과와 계측결과의 차이가 크게 발생하는 것으로 나타났다. 이는 수평방향의 응력-변위거동 모델인 탄소성보법의 한계로써 연직방향으로 심도가 깊어짐에 따라 증가하는 실제 지반의 강성과 응력상태를 반영하지 못한 결과인 것으로 판단된다. 또한 굴착 초기단계의 계측데이터를 적용하는 경우에는 변위 경향이 역해석 결과와 계측결과 간에 큰 차이를 보였다. 그러나 입력하는 계측데이터의 굴착단계가 증가할수록 변위 경향이 비교적 유사해지며 최대 발생변위는 역해석 결과가 계측결과보다 안전측 결과를 도출하는 것으로 검토되었다.

5.3 역해석 축력 결과

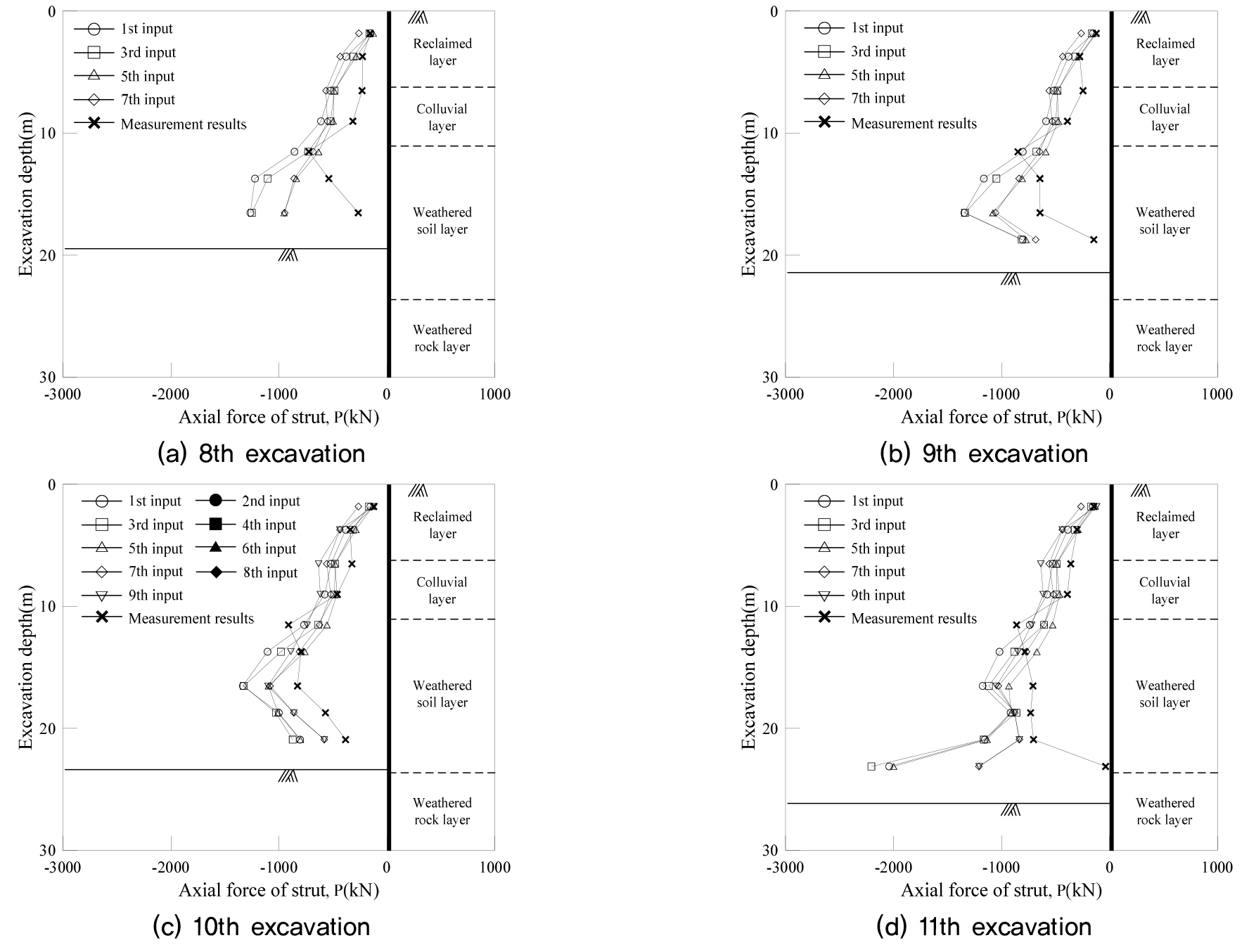
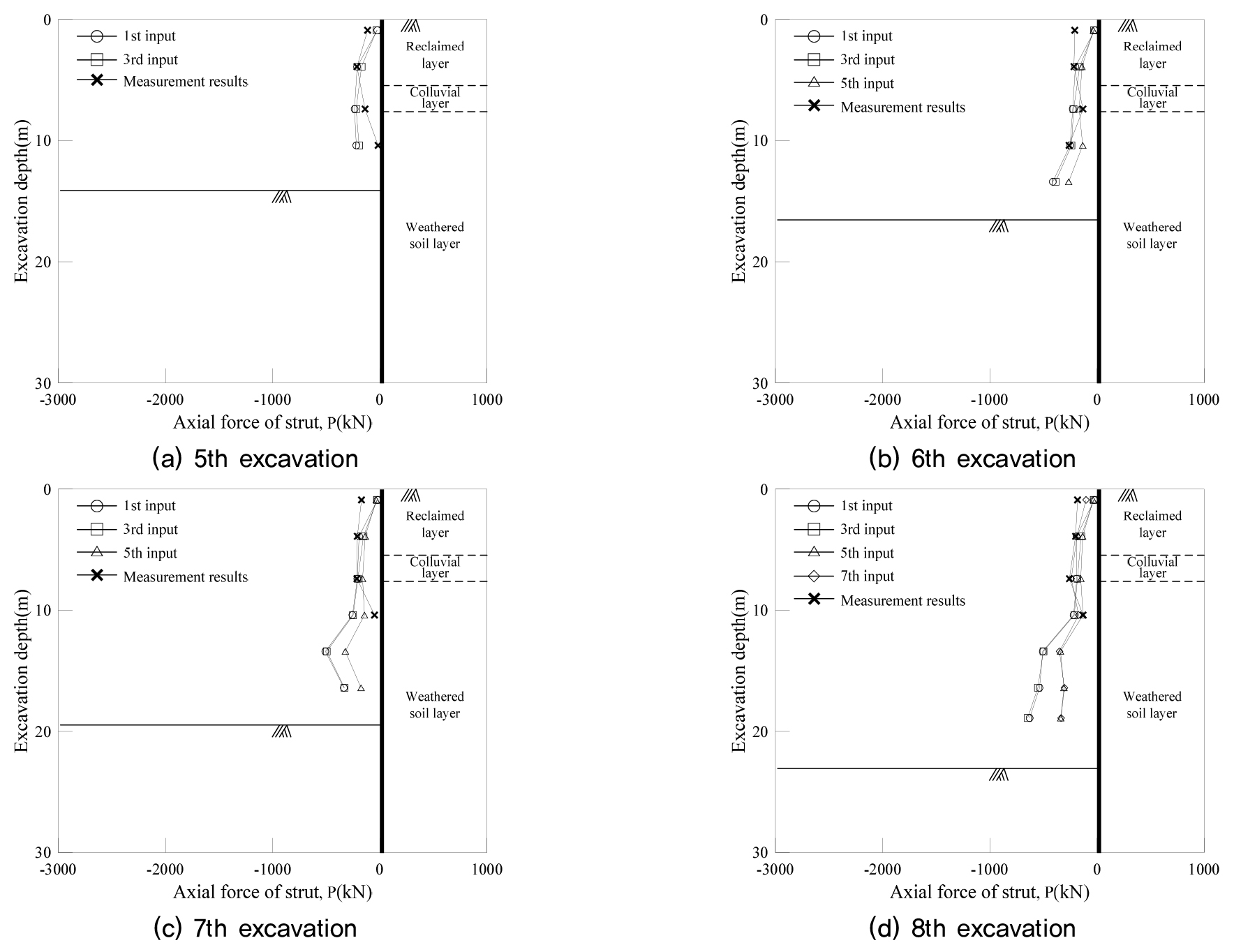
굴착단계별 역해석 결과(Pb)와 계측결과(Pm)의 버팀대 축력은 Fig. 8∼9와 같다. A 현장에 대한 역해석 결과는 굴착 최종 단계인 11단계 굴착시의 흙막이 최대변위는 계측결과의 경우 860.37kN, 역해석 결과의 경우 입력된 계측데이터에 따라 1207.19kN∼2206.33kN 만큼 발생하였다. B 현장에 대한 역해석 결과는 굴착 최종 단계인 8단계 굴착시의 흙막이 최대변위는 계측결과의 경우 257.62kN, 역해석 결과의 경우 입력된 계측데이터에 따라 340.64kN∼646.57kN만큼 발생하였다.

버팀대의 축력 발생 경향은 앞서 검토한 벽체의 변위 결과와 상응하는 결과를 보였다. 굴착심도가 깊어질수록 하부 버팀대의 역해석 결과와 계측결과간에 차이가 발생하였으나 입력하는 계측데이터의 굴착단계가 증가할수록 축력의 경향이 비교적 유사해지는 것으로 나타났다. 최대 발생축력은 역해석 결과가 계측결과보다 좀 더 안전측 결과를 도출하는 것으로 검토되었다.

Fig. 8.

Comparison of strut axial force at field A

Fig. 9.

Comparison of strut axial force at field B

5.4 역해석 결과의 적용성 평가

역해석 프로그램은 흙막이 시공시 초기에 계측된 데이터를 이용하여 중, 후반부의 흙막이 거동을 예측함으로써 인명 및 경제적 재해를 사전에 방지하는 목적으로 활용될 수 있다. 따라서 역해석 프로그램을 효과적으로 활용하기 위해서는 흙막이 가시설의 중, 후반 단계의 변위 예측을 위하여 최소 몇 번째 굴착 단계의 계측데이터를 역해석에 적용하는 것이 가장 잘 계측결과를 유사하게 예측하는지를 파악하여야 한다. 이에 본 절에서는 굴착단계별 계측데이터에 따른 역해석 결과의 적정성 평가를 위해 식 (4)∼식 (5)와 같이 역해석 결과와 계측결과 간의 변위오차(Relative Error of Displacement, RED) 및 축력오차(Relative Error of Axial Force, REF)를 산정하였다.

여기서 δm(max)는 계측결과의 벽체 최대변위(mm), δb(max)는 역해석 결과의 벽체 최대변위(mm)이고 Pm은 계측결과의 버팀대 최대축력(kN), Pb(max)는 역해석 결과의 버팀대 최대축력(kN)이다.

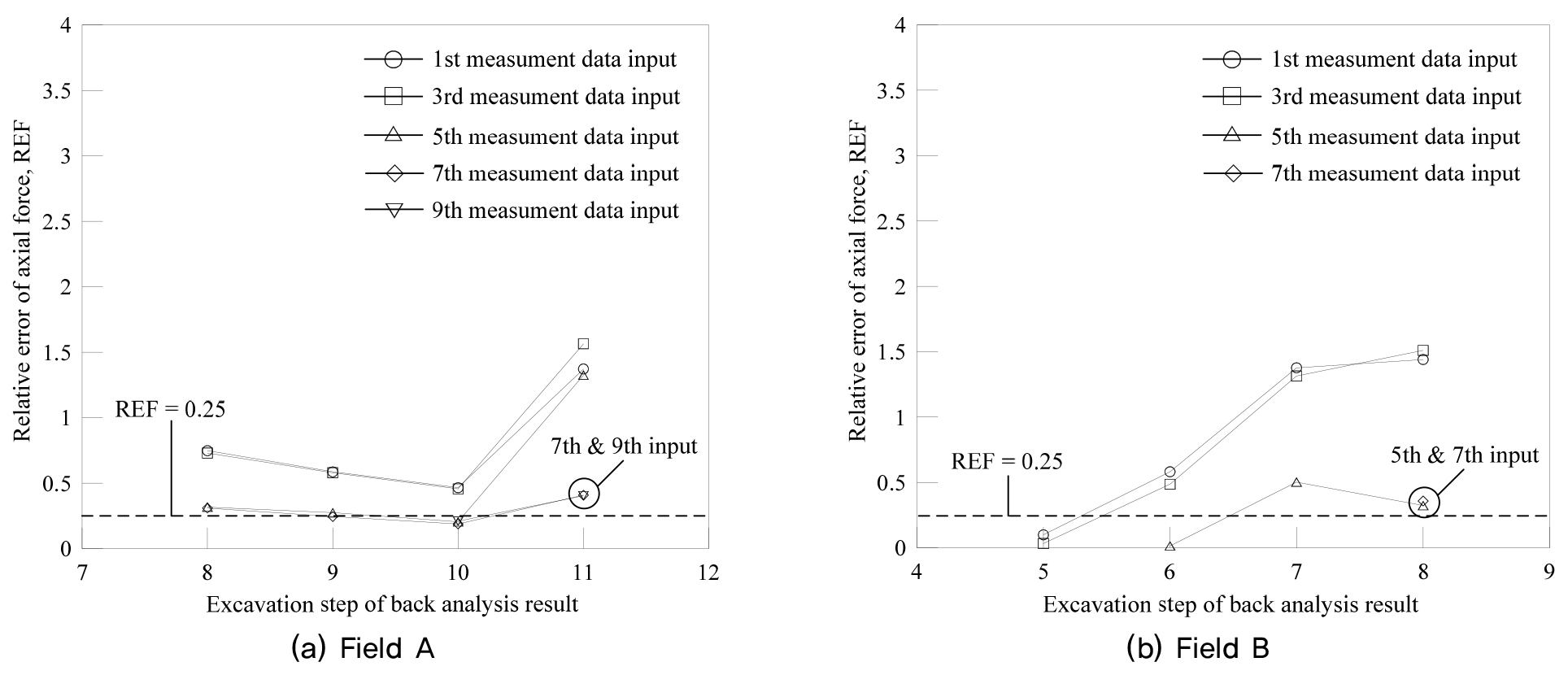
A현장 및 B현장의 변위오차(RED)와 축력오차(REF)를 산정한 결과는 Table 3∼4와 같으며 이를 분석한 결과는 Fig. 10∼11과 같다. 2개의 변위 오차를 분석한 결과 A현장은 굴착 초기단계인 1단계∼5단계의 계측데이터를 적용할 경우 변위오차는 0.021∼1.683이고 축력오차는 0.204∼1.564로 산정되었다. 그리고 B현장은 굴착 초기단계인 1단계∼3단계 계측데이터를 적용하는 경우 변위오차가 0.327∼2.448, 축력오차가 0.033∼1.510으로 산정되어 역해석 결과와 계측 결과간의 괴리가 큰 것으로 나타났다. 이는 초기의 계측 데이터만으로는 다층지반으로 구성되어 있는 실제지반의 거동을 정확하게 반영하기 어렵기 때문으로 판단된다.

그러나 A현장(최종 11단굴착)의 7단계∼9단계 계측데이터를 적용할 경우에는 변위오차가 0.116∼0.370이고 축력오차는 0.188∼0.407로 산정되었다. 그리고 B현장(최종 8단굴착)의 5단계∼7단계 계측데이터를 적용하는 경우에는 변위오차가 0.027∼0.473이고 축력오차는 0.015∼0.503으로 산정되어 역해석 결과와 계측 결과간의 차이가 상당히 근접해지는 것을 알 수 있다. 이 결과는 Bieniawski(1989)가 제시한 변형률은 약 25% 오차가 나타날 수 있다고 제시한 범위의 값을 기준으로 평가해 보면 최종 굴착단계가 11단계인 A현장은 7∼9단계, 최종 굴착단계가 8단계인 B현장은 5∼7단계의 계측데이터를 적용할 경우 오차가 최소로 나타나는 것으로 분석되었다(Fig. 10∼11).

이는 본 현장과 같은 다층지반의 경우 상하부의 지반 물성이 상이하기 때문에 각 지층별 계측데이터가 추가됨에 따라 정밀한 해석이 가능해지기 때문인 것으로 판단된다. 따라서 직접알고리즘 기법이 적용된 역해석 프로그램을 효과적으로 사용하기 위해서는 최종 굴착단계가 8단계∼11단계인 현장을 대상으로 7단계 굴착시의 계측데이터를 입력할 경우 비교적 정확한 흙막이의 거동을 예측할 수 있을 것으로 판단된다.

Fig. 10.

Analysis of Relative error of displacement

Fig. 11.

Analysis of Relative error of axial force

6. 결 론

본 연구는 실제 흙막이 벽체를 대상으로 굴착단계별 계측데이터를 적용하여 역해석을 수행하였으며 직접 알고리즘이 적용된 역해석 프로그램에 대한 적용성을 평가하였다. 그리고 이를 통해 프로그램을 효과적으로 사용하기 위한 활용방안을 제시하였다.

1)직접알고리즘과 유전알고리즘은 모두 흙막이 역해석에 대한 적용성이 높은 것으로 나타났으나 직접알고리즘과 유전알고리즘을 비교할 경우 직접알고리즘이 좀 더 계측치에 근접하는 것으로 평가되었다.

2)굴착심도가 증가함에 따라 벽체 하부구간에서 발생된 벽체변위 및 버팀대 축력은 역해석 결과와 계측결과 간에 큰 차이가 발생하였다. 이는 수평방향의 응력-변위거동모델인 탄소성보법의 한계로써 연직방향으로 심도가 깊어짐에 따라 증가하는 실제 지반의 강성과 응력상태를 반영하지 못한 결과인 것으로 판단된다.

3)각 현장의 변위오차(RED)는 초기 굴착단계 계측데이터를 적용시 0.021∼2.448, 후반부 굴착단계 계측데이터를 적용시 0.027∼0.473으로 산정되었으며 축력오차(REF)는 초기 굴착단계 계측데이터를 적용시 0.033∼1.564, 후반부 굴착단계 계측데이터를 적용시 0.015∼0.503으로 산정되어 초기 계측데이터 보다는 후반부 계측데이터를 역해석 적용할 경우 좀더 정확한 해석이 이루어질 것으로 판단된다.

4)최종 굴착단계가 11단계인 경우 7∼9단계, 최종 굴착단계가 8단계인 경우 5∼7단계의 계측데이터를 입력할 경우 비교적 정확한 흙막이의 거동을 예측할 수 있었다. 따라서 직접알고리즘 기법이 적용된 역해석 프로그램을 효과적으로 사용하기 위해서는 최종 굴착단계가 8단계∼11단계인 현장을 대상으로 7단계 굴착시의 계측데이터를 입력하여 예측하는 것이 적절할 것으로 판단된다.

본 연구에서는 2개소의 현장계측 데이터를 이용한 결과의 한계로 정성적인 결론을 도출하였으나 추가적인 계측데이터의 수집과 역해석 데이터의 구축을 통한 보완 연구가 요구된다.