1. 서 론
2. 지반 변형 대응형 말뚝 기초 개발
2.1 지반 변형에 따른 말뚝 영향
2.2 개발 말뚝 기초의 원리 및 작동 메커니즘
3. 수치해석 절차 및 해석 케이스 설정
3.1 실린더의 수축, 이완 모사를 위한 열팽창 모델 적용
3.2 지반 변형 모사 및 해석 케이스 설정
4. 해석 결과 및 실효성 검증
4.1 해석 지반에서 말뚝의 극한하중 선정
4.2 지반 융기에 따른 말뚝 거동 분석
4.3 지반 침하에 따른 말뚝 거동 분석
5. 결 론
1. 서 론
2019년 글로벌 해외건설시장은 5,000억 달러에 육박한 것으로 추정되며, 대규모 인프라시장이 구축될 것이라 보고 있다(Kang, 2020). 노후화된 인프라 구조물 교체 및 교통 인프라 건설 수요와 맞물려 아시아권에서는 인도네시아, 라오스, 중국 및 실린더의 팽창 조건은 말뚝에 작용하는 인장 응력을 분담해 주어 전체적으로 말뚝에 작용하는 축 응력을 감소시켰다. 지반 침하는 부주면 마찰력 발생에 따른 말뚝의 압축응력을 증가시켜 주었는데, 실린더는 중립점 이하에 위치하여 수축 거동 시 최적의 효율을 보여주었다. 하지만 지반 변형 대응형 말뚝 시공 시 수축 및 팽창량은 상부 구조체의 허용 변위 범위를 준수하여야 하며, 설계 시 이에 따른 고려가 필요할 것으로 판단된다. Keywords : Ground deformation, Heaving and Settlement, Cylinder, Shrinkage and expansion, Numerical analysis 중동 국가에서 대규모 인프라 건설에 나서고 있으며, 유럽, 캐나다 뿐 아니라 아프리카에서도 수백억 달러 규모의 공사가 진행 중 혹은 계획에 있다(Yoon, 2018). 인프라 구조물은 사회적 생산 기반. 또는, 경제 활동의 기반을 형성하는 기초적인 시설로 댐・도로・항만・발전소・통신 시설 등의 산업 기반 및 학교・병원・공원 등의 사회 복지・환경 시설이 이에 해당한다. 인프라 구조물 특성상 대규모의 토목 구조물 건설이 이루어지며, 구조물의 지지력 확보를 위한 말뚝 기초 시공이 필수적이다. 하지만 인프라 구조물의 주요 수용처는 극한지 및 극서지와 같은 지역이 될 가능성이 큰 상태이며, 해당 지역의 지리적, 환경적 요인으로 인해 지반 변형이 발생 할 수 있다.
극한지는 최소 2년 이상 장기간에 걸쳐 토양 온도가 물의 어는점인 0°C 이하로 유지되어 얼어붙은 영구 동토와 계절에 따라 얼고 녹음(동결, 융해)이 반복되는 계절적 동토로 구분된다. 영구 동토에서는 지하수의 동결로 인한 지반 융기가 발생 할 수 있으며, 계절적 동토에서는 동결・융해에 따른 융기/침하 발생 가능성이 존재한다. 극서지는 주로 중동과 같은 적도층에 위치하는데 해당 지역은 열대우림을 비롯한 연약층이 다수 분포되어 있어 침하가 예측된다. 남미 및 동남아시아와 같은 열대우림 지역은 주로 점토층으로 이루어진 연약지반 층이 두껍고 암반층이 깊게 위치하고 있으며 강우량이 매우 많아 지반의 함수비가 높다. 이러한 지반의 상부에 구조물이 건축될 경우, 구조물 하중에 의하여 점토층의 간극수가 빠져나가 압밀이 발생할 가능성이 높다.
지반의 융기 및 침하에 따른 말뚝내 영향 분석 및 저감 방법에 대한 국내・외 연구는 활발히 진행되어져 왔다. 지반 융기 시 말뚝 시공과 관련된 국내 논문은 주로 융기가 발생하는 지반에서의 보강방법 혹은 지하 터파기로 인한 융기 가능성 검토가 주를 이루고 있으며, 해외에서는 부가적인 요소를 말뚝에 결합하여 융기를 억제한다거나 지반 자체 개량 등이 수행되었다(Hong et al., 2004; Bae et al., 2006, Lee, 2010; Mohamedzein et al., 1999; Rao et al., 2007; Aljorany et al., 2014). 지반 침하 시 말뚝 시공과 관련된 국내 연구는 부주면 마찰력이 발생하는 말뚝을 대상으로 다양한 조건에서의 데이터 수집과 현황 분석 및 지지력 공식 분석을 수행하였으며, 저감 공법으로는 Bitumen과 같은 역청재의 도포가 제시되기도 하였다(Ko et al., 2010; Lee et al., 2010; Hong, 2012). 국외에서는 국내와 달리 현황 분석보다는 저감 효과에 대한 분석이 수행되었으며, 말뚝 주면에 도포하는 물질 종류 및 두께 등을 해석 또는 실험을 통해 분석하였다(Tawfiq and Caliendo, 1995; Chen et al., 2009; Feng et al., 2019).
하지만 다양한 연구에서 지반 변형에 대해 대응이 가능한 새로운 말뚝 형식을 제안하는 연구는 진행되지 않았다. 따라서 본 연구에서는 극한지와 극서지에서 발생할 가능성이 높은 지반 변형에 대하여 말뚝 및 상부 구조체에 미치는 영향을 최소화하기 위해 새로운 형식의 말뚝 기초를 개발하고자 한다. 지반 대응형 말뚝 기초는 말뚝과 변형 감지가 가능한 팽창/수축 실린더가 결합된 상태로 각 지반 변형에 대해 유연한 대처가 가능할 것으로 판단된다. 이를 검증하기 위해 수치해석을 이용하여 각 지반 변형 조건에 따라 실린더의 수축 및 팽창량을 말뚝의 다양한 깊이에서 발현시키고, 이에 따른 말뚝 거동을 분석하였다. 현재 연구 단계는 지반 대응형 말뚝 기초 개발 전 지반 내 거동 메커니즘을 수치해석적으로 분석한 것으로 이를 토대로 한 말뚝 제작이 차년도에 수행될 예정이다.
2. 지반 변형 대응형 말뚝 기초 개발
2.1 지반 변형에 따른 말뚝 영향
극한지와 극서지는 기후적, 환경적, 지리적 요건에 따라 지반이 상승하는 융기와 지반이 하강하는 침하 문제가 발생할 가능성이 크다. 이는 지반 내 안정성을 저해하고 구조물의 안정성을 위해 시공되는 말뚝 기초의 성능을 감소시킬 수 있다.
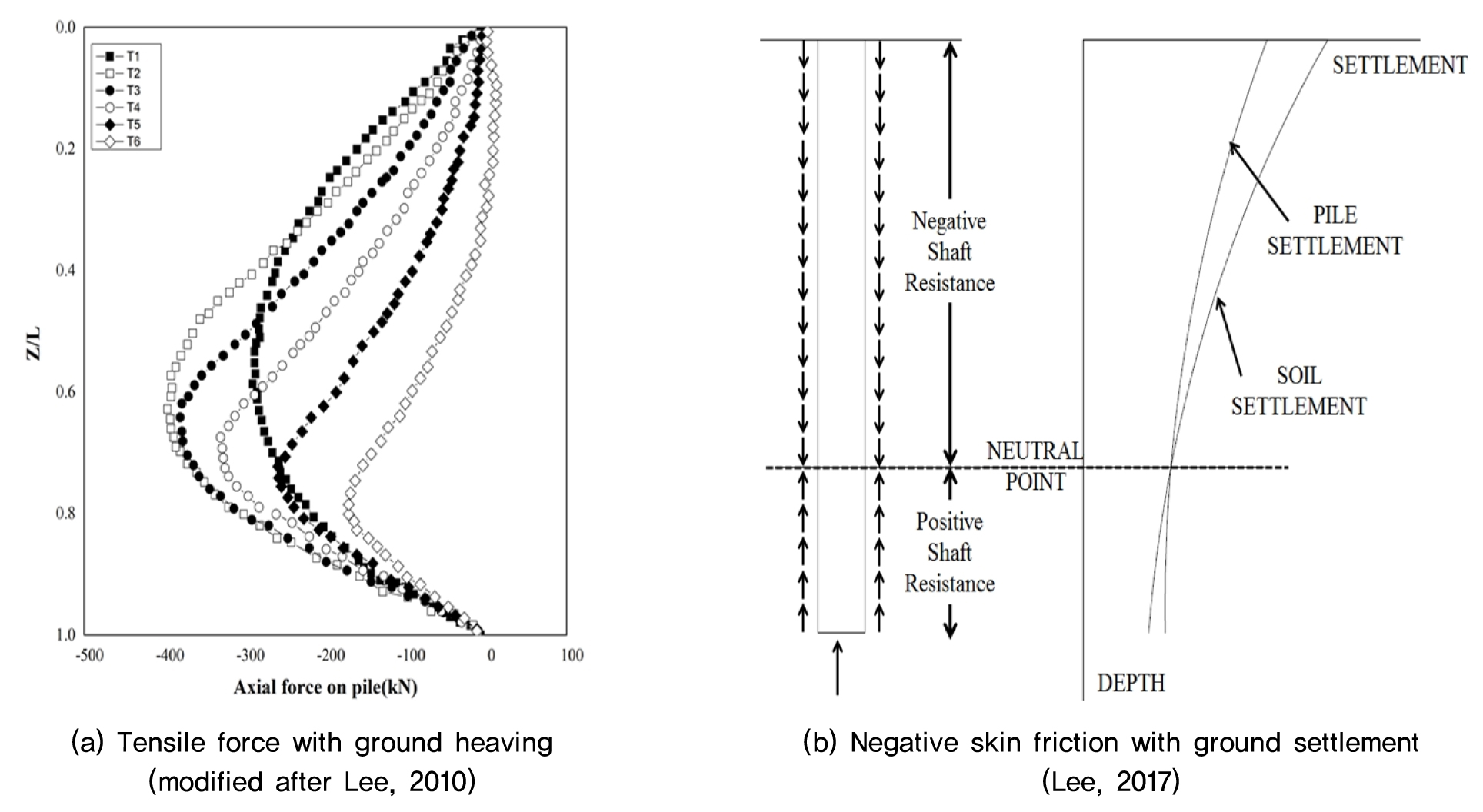
지반 융기 시 말뚝에는 상향의 변위가 발생하고 이로 인한 주변 지반 교란에 따라 말뚝의 균열 및 변위가 발생한다. 이때 발생하는 상향 변위는 말뚝에 인장력으로 작용하게 되는데, 점차적으로 말뚝의 항복 발생 구간을 확장 시키기 때문에 사용성을 감소시킨다는 단점이 있다. Lee (2010)에 따르면 말뚝에 발생하는 최대인장력은 말뚝의 중앙부 혹은 선단부에서 발현되며, 말뚝의 선단에서는 0에 가까운 축력이 발생하는데 이는 말뚝 선단과 선단부 지반 사이에 상대 변위로 인하여 공간(gap)이 발생하기 때문이다(Fig. 1(a)).
지반 침하 시 말뚝에는 주면을 끌어내리는 부주면 마찰력이 작용한다. 부주면 마찰력은 말뚝에 연직 하중으로 작용하여 추가적인 내력을 발생시키고 이에 따라 말뚝의 성능이 감소하게 된다. 부주면 마찰력의 주요 원인으로는 말뚝과 주변 지반의 상대적인 변위 차이로 정의 할 수 있으며 이는 Fig. 1(b)와 같은 메커니즘으로 발생한다(Lee, 2017). 말뚝 주면을 따라 중립점(Neutral point)까지 지반은 말뚝보다 더 많은 침하가 발생하며, 상대적인 변위 차이로 발생한 전단 응력은 말뚝상단에서 중립점까지 말뚝을 아랫방향으로 끌어내리게 된다. 중립점은 말뚝과 지반의 상대적인 움직임이 0인 곳을 의미하며, 지반의 침하량이 말뚝의 하향 방향 움직임과 같은 지점이다. 만약 말뚝의 선단이 견고한 층에 근입된다면 말뚝의 하향 변위는 말뚝의 압축성 때문에 발생하기 때문에 중립점은 지표면에서 더 멀리 위치하게 된다.
2.2 개발 말뚝 기초의 원리 및 작동 메커니즘
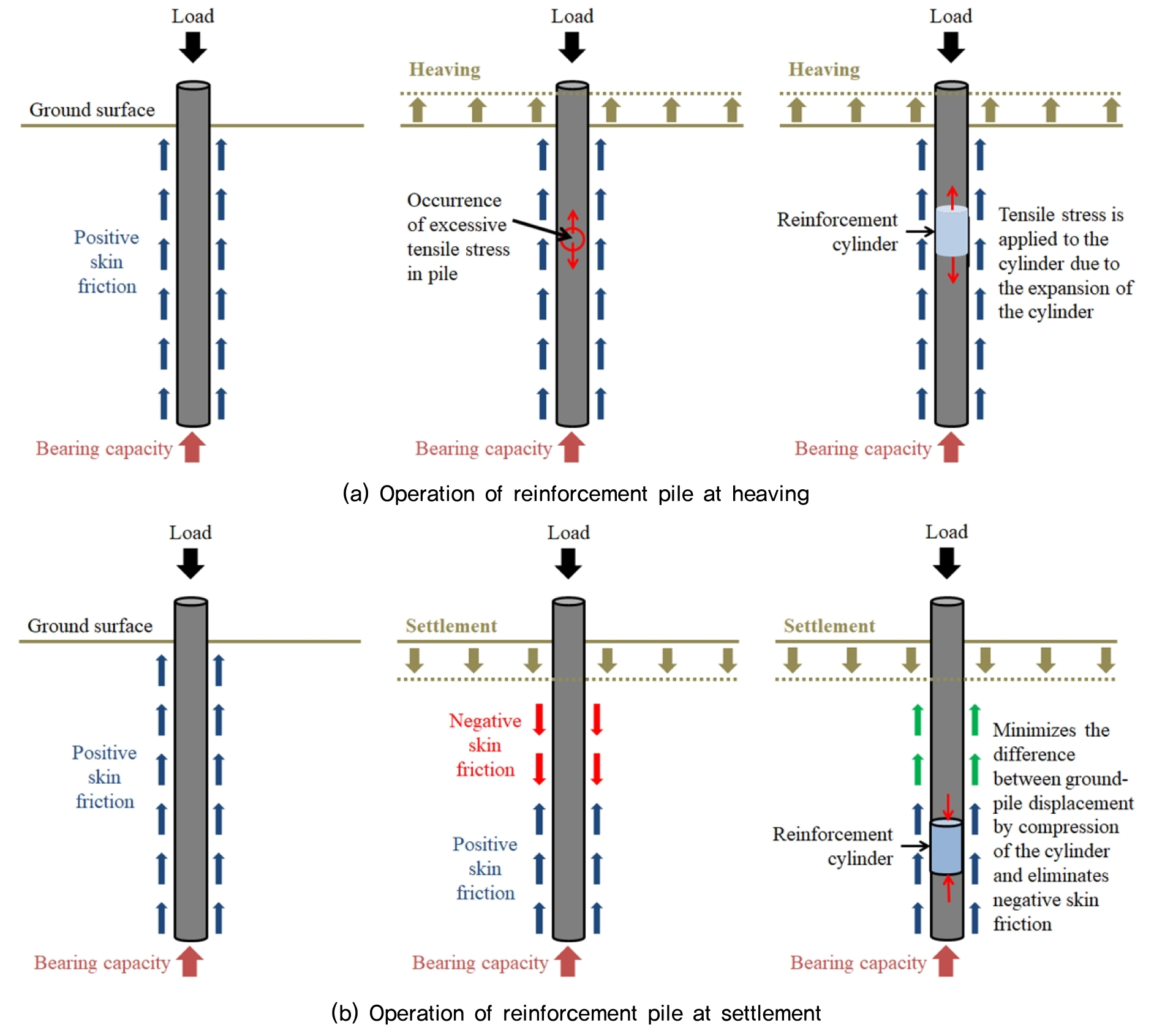
지반 변형 대응형 말뚝 기초의 개발 원리는 지반의 융기 또는 침하가 일어났을 때 발생하는 말뚝과 지반 접촉면간의 상대적인 변위와 이로 인한 미끌림(Slip)을 최소화하고 말뚝 자체에 미치는 영향을 줄이는 것에 있다. 따라서 말뚝에 삽입되는 보강 실린더는 변형 발생에 따른 힘과 변위를 억제 하는 것을 주목적으로 하며, 지반 융기 및 침하 시 개발 말뚝의 작동 메커니즘은 Fig. 2와 같다.
융기 발생 시 말뚝에 미치는 중요 문제점은 인장력에 따른 말뚝 파손이다. 지반의 융기가 발생하면서 말뚝 주면에 위치한 흙들이 말뚝 자체를 밀어올림에 따라 말뚝 주면에는 상향력이 발생하지만 이러한 상향력은 말뚝 지지력을 증가시키는 것이 아닌 말뚝 자체의 인장력을 증가시켜 구조체의 파괴를 유발한다. 따라서 융기에 의한 상향력(인장력)이 말뚝 주면에 작용 할 경우 말뚝 내부에 삽입된 보강재가 자체적으로 팽창하여 인장력을 받게 된다. 지반의 침하가 발생할 경우 말뚝 주면에 위치한 흙들이 말뚝 자체를 끌어내림에 따라 말뚝 주면에는 하향력(부주면 마찰력)이 발생하게 되고 이는 말뚝에 추가적인 압축력으로 이어진다. 하지만 지반 변형 대응형 말뚝 기초는 이에 대응하여 아래로 작용하는 하향력(압축력)이 말뚝 주면에 작용 할 경우, 말뚝 내부에 삽입된 실린더가 자체적으로 수축하여 말뚝-지반의 상대적인 변위차를 최소화 하고, 부주면 마찰력을 소거하게 된다.
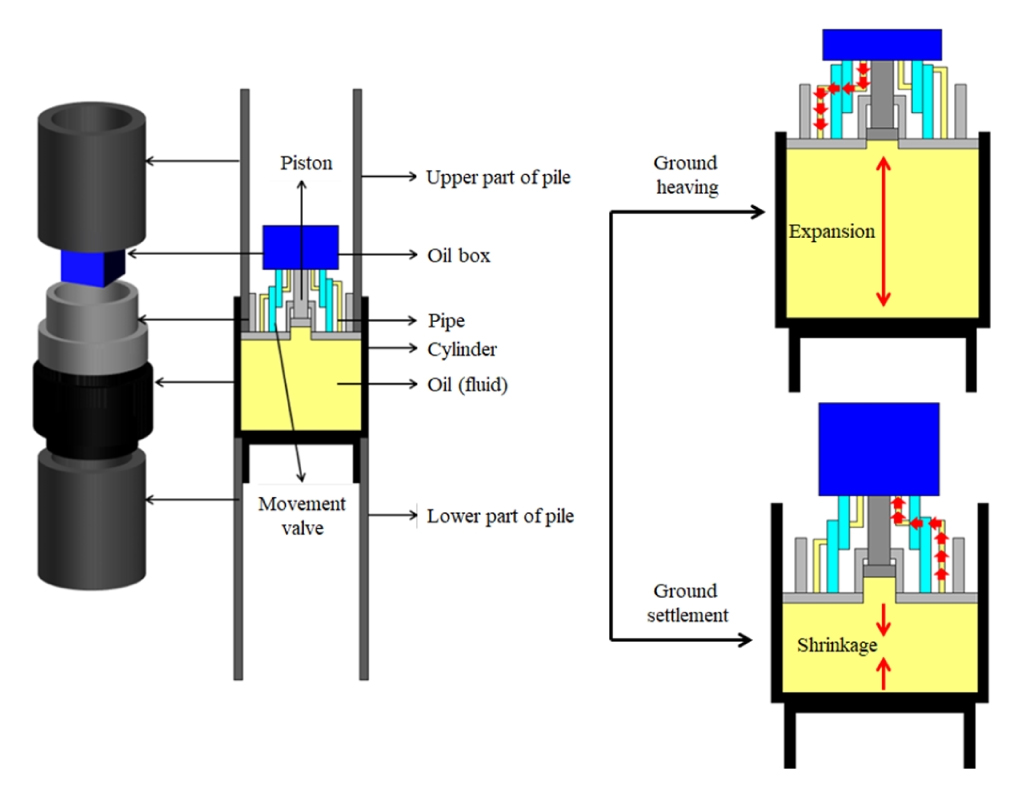
실린더형 보강재의 구성 및 구동 메커니즘은 Fig. 3과 같다. 실린더형 보강재는 실린더, 실린더 내부의 유체, 피스톤, 밸브, 유관 등으로 구성된다. 지반이 융기하는 경우 상부 말뚝이 위로 끌려 올라가게 되며, 실린더 내부의 압력이 감소하여 피스톤에 하향 변위가 발생하게 된다. 이로 인하여 벨브의 한쪽 관이 열리게 되고, 압력차로 인해 관을 통해 oil box 내부의 유체가 실린더로 이동하며 실린더가 인장된다. 지반의 침하가 발생하면 하면 상부 말뚝이 아래로 밀려 내려오게 되며, 실린더 내부의 압력이 증가하고 피스톤에 상향 변위가 발생한다. 이 때 밸브의 한쪽 관이 열리면서 실린더와 oil box 사이의 압력차로 실린더 내부의 유체가 oil box로 이동하게 되고 실린더가 압축된다. 압력이 안정화 될 때까지 유체의 이동 후 피스톤이 제자리로 돌아오게 되며 최종적으로는 실린더가 일정량 압축된 상태가 된다.
3. 수치해석 절차 및 해석 케이스 설정
3.1 실린더의 수축, 이완 모사를 위한 열팽창 모델 적용
본 연구의 수치해석 과정에서는 밸브의 작동 과정 및 세부 설계는 진행하지 않았으며, 실린더의 팽창 및 수축 과정을 해석 프로그램 내 열팽창 모델을 사용하여 모사하였다. 밸브 모사를 수행하지 않은 이유는 해석의 간편성을 위해서이며, 본 연구의 목적이 밸브의 구동 가능성을 평가하는 것이 아닌 말뚝에 실린더를 결합하였을 때 지반 변형에 대응 가능 여부를 분석하는 것이기 때문이다.
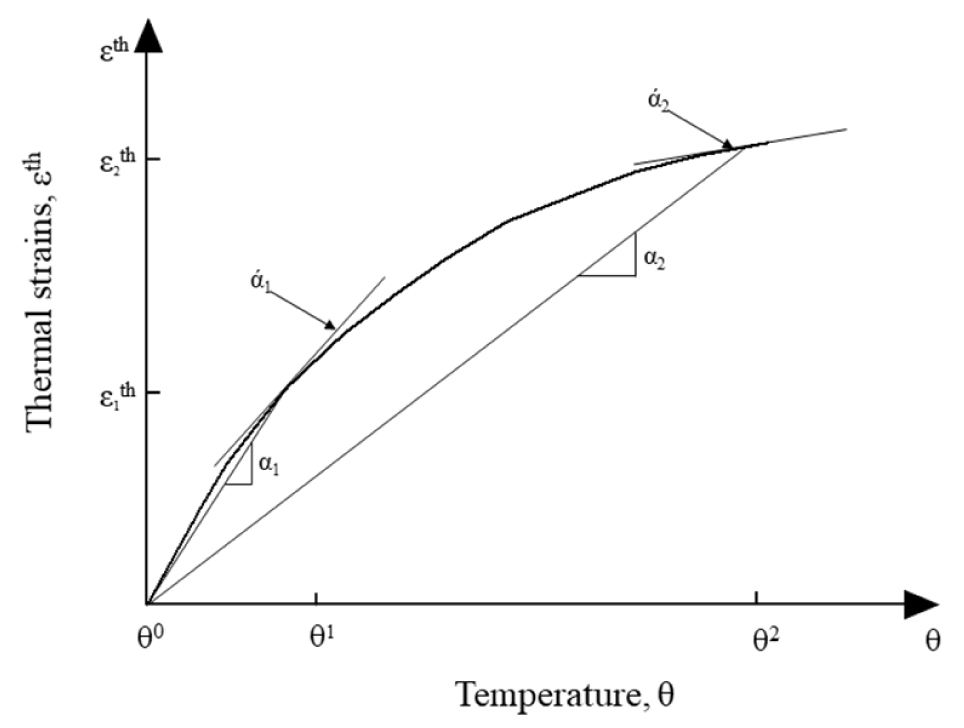
열팽창 모델은 열팽창 계수와 온도 변화에 따른 균질한 연속체 요소의 부피 변화를 나타내는 것으로 수치해석 프로그램인 ABAQUS/CAE (SIMULIA, 2014)에서는 이러한 특성을 식 (1)과 Fig. 4로 정의하고 있으며, 부피 변형률을 열팽창 계수와 온도 변화에 따른 함수로 나타낸다.
여기서, εth : 열팽창 변형율
α : 열팽창계수
θ : 현재 온도
fβ : 사전에 정의된 필드변수
θ0 : 기준 온도
θI : 초기 온도
fβI : 사전에 정의된 필드변수 초기 값
열팽창 변형률은 재료 자체의 물성인 탄성계수, 밀도 등과는 상관이 없으며, 임의로 부여한 온도 변화(기준 온도와 초기 온도의 차이)와 열팽창계수와 관련이 있다. 동일한 팽창 또는 수축을 모사한다고 하더라도 온도 변화 값이 변하면 열팽창계수도 변하기 때문에 해석의 간편성을 위해 온도 변화를 임의의 변화 값인 0°C(기준 온도)에서 10°C로 고정하였다.
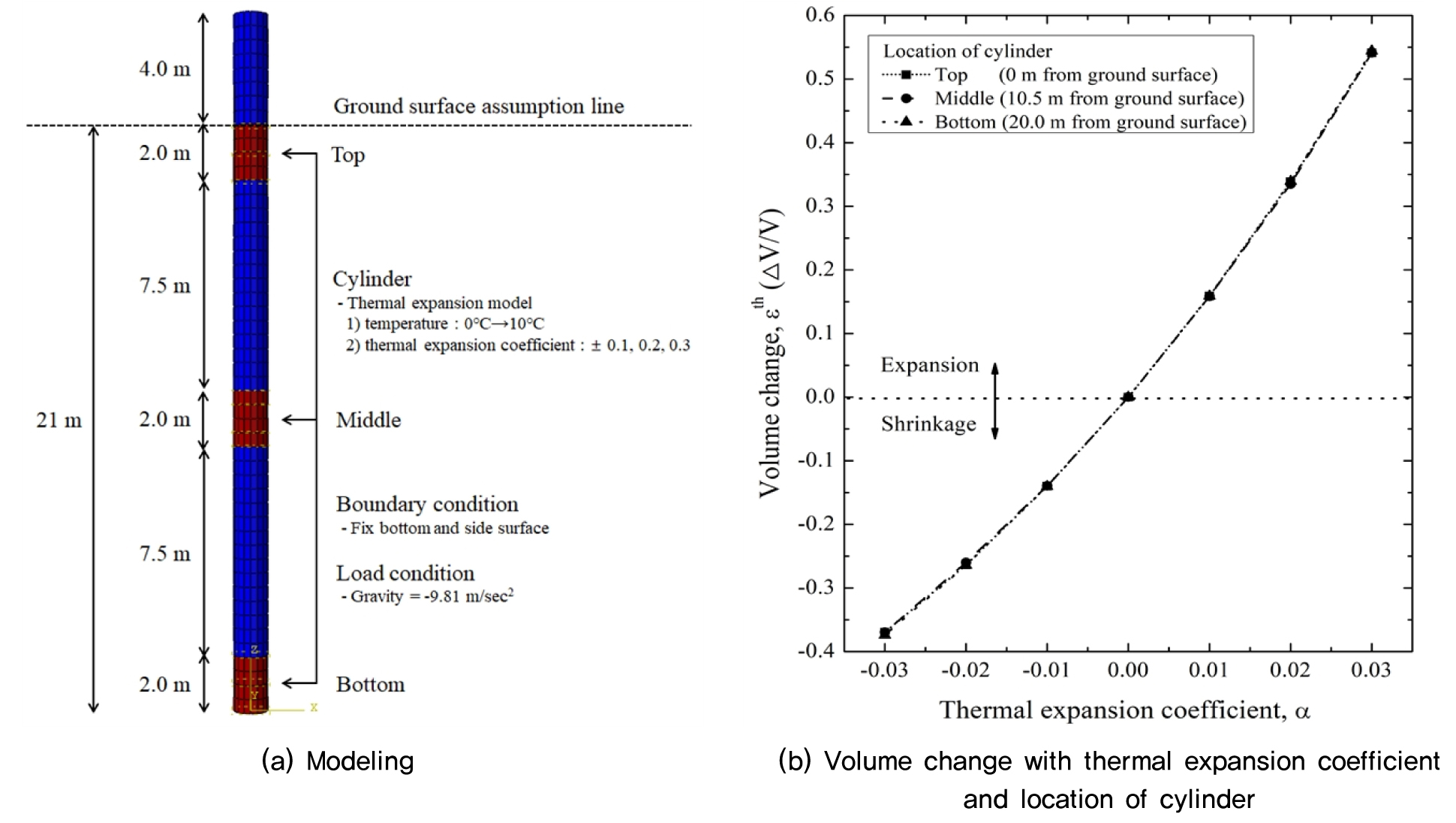
이에 따라 해석 모델링은 Fig. 5(a)와 같다. 실린더는 말뚝 상단, 중단, 하단에 1 m 두께로 삽입하였으며, 열팽창계수에 따른 부피 변화 값을 Fig. 5(b)와 같이 분석하였다. 실린더가 삽입될 말뚝의 경우 항타 또는 타설 말뚝이 불가능한 형태이기 때문에 기성 말뚝인 강관 말뚝을 대상으로 하였으며, 가장 기본적인 형태로 직경 609.6mm, 두께 14mm, 길이 25m로 모델링하였다. 강관말뚝의 물성은 SKK400 강관말뚝의 물성인 탄성계수 117,680MPa, 포아송비 0.3, 밀도 7.86t/m3을 적용하였으며 실린더의 경우 강관말뚝과 같은 물성을 사용하나 열팽창모델이 추가적으로 입력된다. 이때 말뚝 상단의 경우 이후 지반 내 관입될 것을 고려하여 지표면 바로 아래 지점으로 지정하였고, 이는 말뚝 두부로부터 4m 지점이다.
부피 변화비는 ΔV/V로 V는 초기 실린더의 부피이며, ΔV는 열팽창 이후 실린더의 부피를 의미한다. 해석 결과, 양(+)의 열팽창 계수를 입력하였을 경우 팽창하였으며, 음(-)의 열팽창 계수를 입력하였을 경우 수축하는 것을 확인하였다. 만약 온도 변화가 +10°C가 아닌 –10°C로 하였을 경우 반대 부호가 나타난다. 열팽창 계수에 따른 부피 변화비는 선형이 아닌 곡선 형태를 가지고 있으며, 부호를 바꾼 동일한 값을 입력하더라도 부호만 바뀌는 부피 변화비를 가지지 않았다. 따라서 열팽창 해석은 수축 과정보다 팽창이 조금 더 열팽창 계수에 대해 민감함을 알 수 있다. 또한, 중력 값이 작용함에도 불구하고 실린더의 위치에 따른 부피 변화비는 차이를 보이지 않았다. 이를 통해 열팽창 모델은 연속체 요소의 부피 변화만을 모사한다는 것을 입증 할 수 있다.
3.2 지반 변형 모사 및 해석 케이스 설정
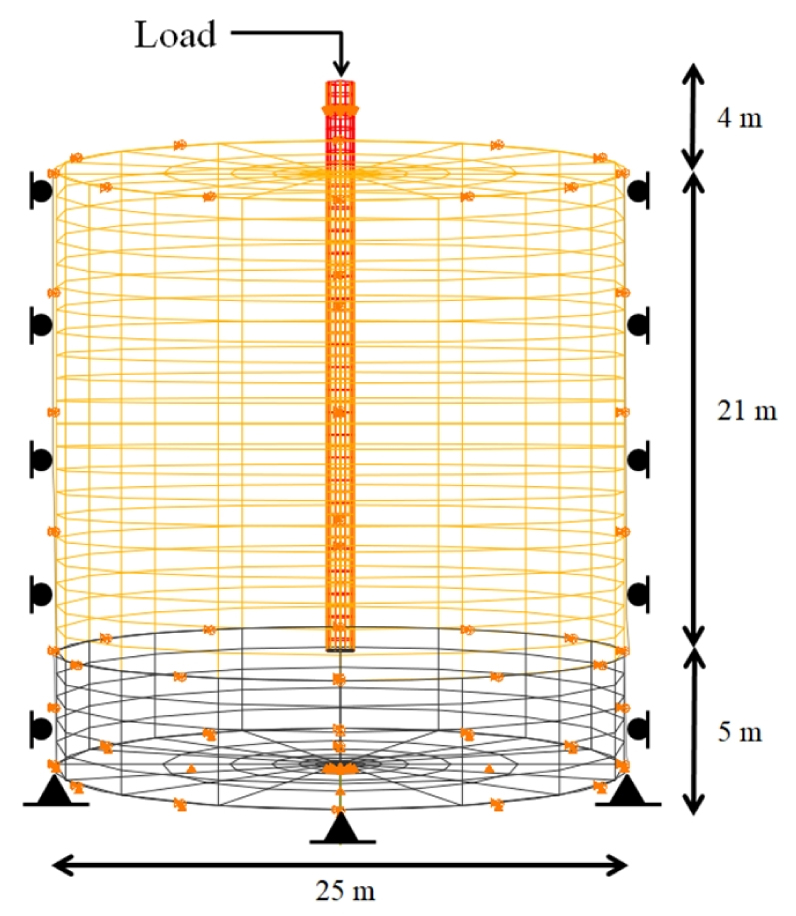
지반 변형 대응형 말뚝 기초의 실효성을 검증하기 위해 지반을 Fig. 6과 같이 모델링 하였다. 모델링된 지반은 원기둥 형태로 단말뚝의 응력 분포 범위를 충분히 포함 할 수 있도록 지름 25.0m, 높이 26.0m(연약점토층 = 21.0m, 암반층 = 5.0m)로 구성하였다. 지반 변형 대응형 말뚝 기초는 암반층(풍화암) 바로 위에 근입되며, 강관말뚝 내부의 폐색된 흙은 없는 것으로 가정하였다. 이때 사용된 물성은 Kim et al.(2020)의 문헌을 참고하였다(Table 1).
Table 1.
Material properties (Kim et al., 2020)
경계 조건은 지반 하단면을 높이 방향으로 고정하여, 아래 방향으로의 처짐이 발생하지 않도록 하였으며, 지반 옆면은 좌우측 고정을 통해 옆면으로의 움직임이 없으나 높이 방향으로의 움직임은 가능하도록 설정하였다. 요소(mesh)는 지반과 말뚝의 변형 요소를 고려하여 C3D8R(An 8-node ilinear brick, reduced integration, hourglass control)을 사용하였으며, 말뚝의 경우 주면 마찰력을 비롯한 응력 요소들을 측정해야하기 때문에 지반 보다 상대적으로 조밀하게 구성하였다.
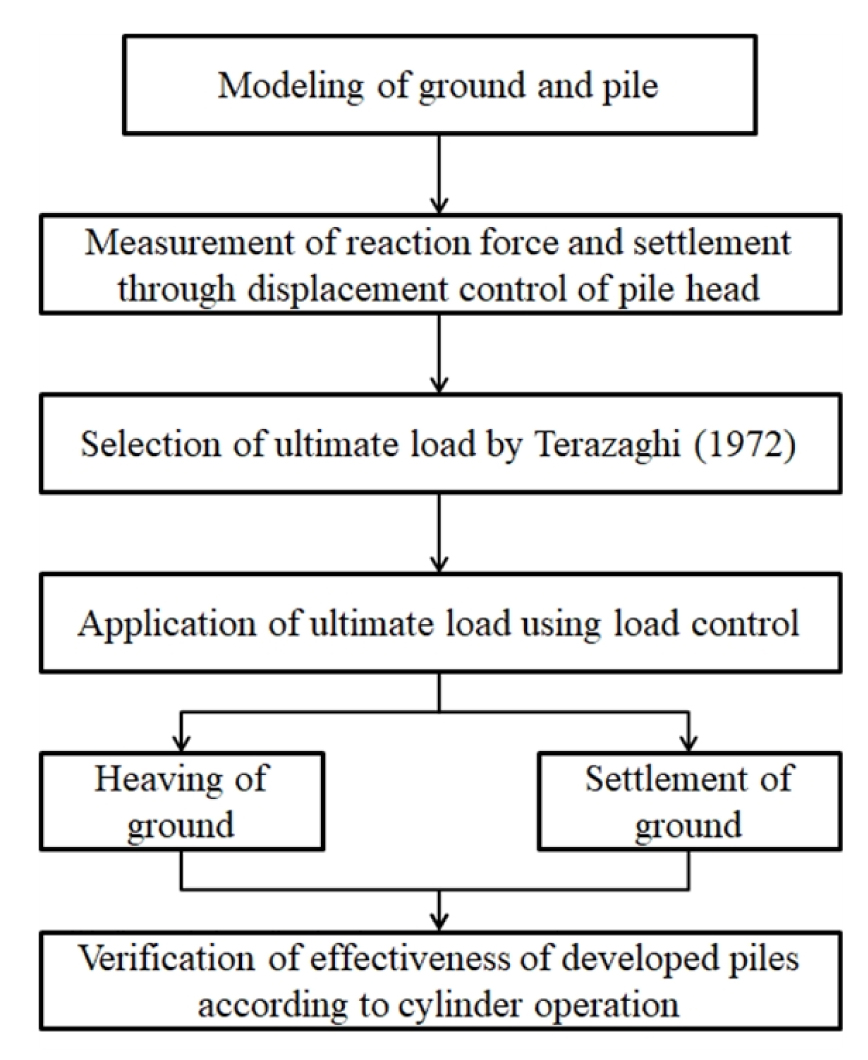
해석 과정 및 케이스 설정은 Fig. 7과 같다. 우선적으로 말뚝에 재하되는 하중을 결정하며, 이는 말뚝 두부 변위제어에 따른 반력 측정을 수행한다. 말뚝 설치의 목적이 상부 구조물 하중에 따른 지지력 발현이기 때문에 하중 재하는 필수적이다. 하지만 충분한 하중이 재하되지 않을 경우 말뚝의 거동을 정확히 분석할 수 없으며, 과도한 하중은 말뚝 자체의 손상을 유발하기 때문에 적절한 하중 선택이 중요하다. 이에 따라 재하 하중을 재료의 파괴가 발생하기 직전의 하중인 극한하중으로 선정하였으며, 극한하중 작도법 중 강관말뚝에 사용하기 적합한 Terzaghi(1942) 이론에 근거한 극한하중 선정법을 사용하였다. Terzaghi(1942) 이론은 말뚝의 극한하중을 침하량이 말뚝 직경에 10%에 도달 할 때의 하중이라고 정의하며, 본 연구에서는 강관말뚝 직경이 609.6mm 이기 때문에 침하량 60.96mm에서의 하중을 극한하중으로 선정하였다.
극한하중 선정이 완료되면 변위 제어가 아닌 하중 제어를 수행한다. 이때 하중은 선정된 극한하중을 강관말뚝 단면적으로 나눈 값으로 Pa 단위이다. 하중 제어를 수행하는 이유는 변위 제어 시 지반 변형에 대해 말뚝 두부가 고정되는 현상이 발생하며, 이는 지반 융기/침하에 따른 말뚝 변위를 정확히 측정하기 어렵기 때문이다. 따라서 하중 제어 이후 지반의 침하와 융기를 강제적으로 발생시켜 지반 변형을 유도하며, 실린더 위치 및 팽창/수축량을 변수로 지반 대응형 말뚝 기초의 실효성을 검증한다.
4. 해석 결과 및 실효성 검증
4.1 해석 지반에서 말뚝의 극한하중 선정
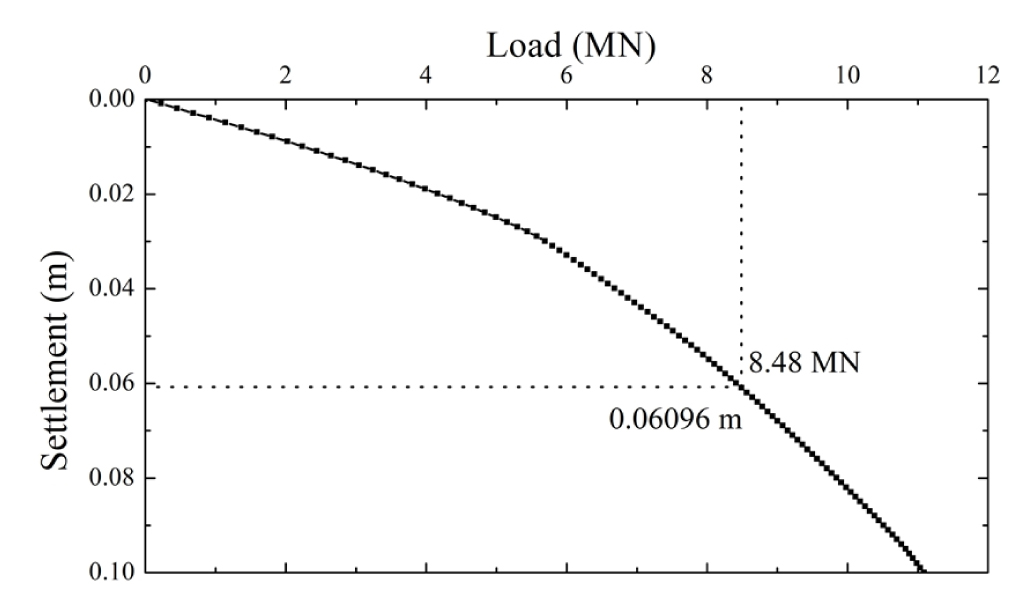
지반 변형 대응형 말뚝의 극한하중은 실린더를 강관말뚝의 물성과 동일하게 설정하였으며, 온도에 따른 팽창만 가능하도록 모델링했기 때문에 일반적인 강관말뚝의 극한하중과 같다. Fig. 8은 지반 변형이 발생하지 않았을 때 말뚝 두부 변위 제어에 따른 하중-침하 곡선을 나타내며, Terzaghi(1942)의 극한하중 선정법에 따라 해석에 사용된 말뚝의 극한하중은 8.48MN이다. 이후 해석에서는 극한하중을 압력단위로 변경하여 입력되며, 강관말뚝의 단면적을 고려하여 압력 값은 323.67MPa이다.
4.2 지반 융기에 따른 말뚝 거동 분석
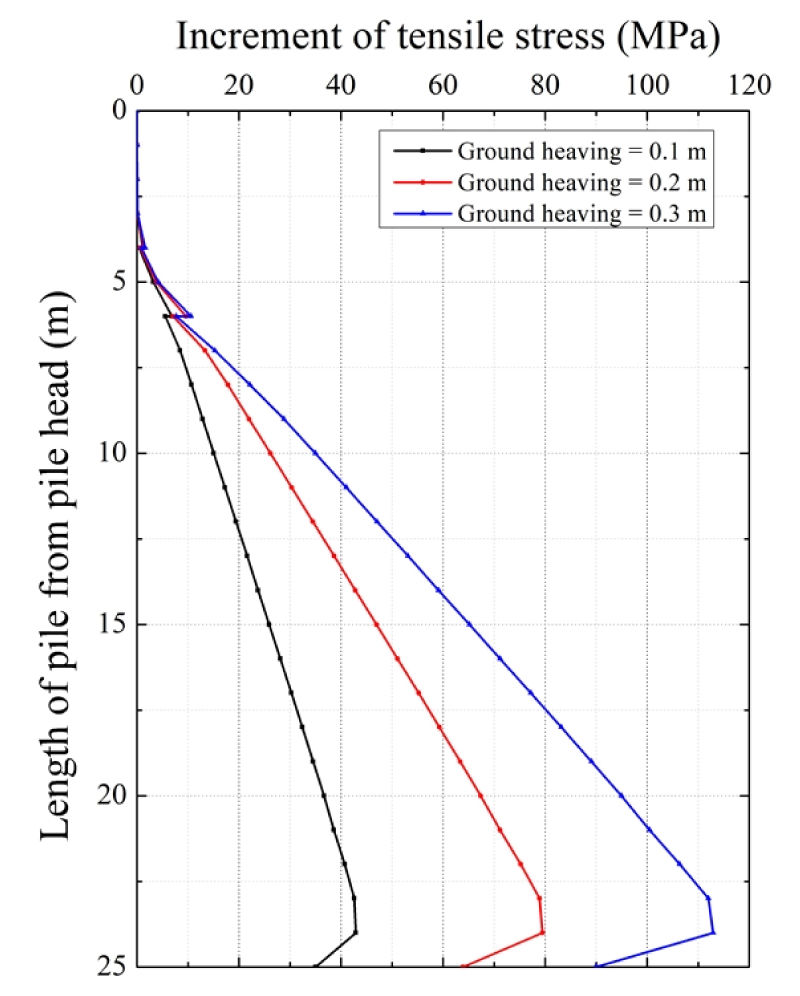
지반 융기에 따른 말뚝의 거동은 지지력 저하적인 측면보다는 말뚝 자체의 인장 응력과 관련이 있으며 과도한 인장 응력은 말뚝의 내구성에 큰 영향을 준다. 지반이 융기 할 때 마찰력은 지반의 상향 움직임으로 인하여 증가하는 경향을 나타내기 때문에 지반 융기에 따른 말뚝 거동 분석에서는 융기량에 따른 인장 강도만을 측정하였다(Fig. 9). 초기 인장강도와 비교하여 융기량에 따른 인장 응력 증가량은 융기가 많이 일어날수록 크게 발생하였다. 접촉면이 없는 상부를 제외하고 인장 응력이 발현되기 시작하였으며, 24m 길이에서 최대 인장 강도가 발현되었다. 융기량이 0.1m일 경우 최대 인장 응력은 42.88MPa이며, 0.2m 에서는 79.47MPa, 0.3m에서는 112.92MPa이다. 0.1m 융기 발생 시와 비교하였을 때 0.2m에서는 185%가 발현되며, 0.3m에서는 263%가 발현되어 지반 융기 시 말뚝은 인장 응력 증가에 취약함을 알 수 있다. 또한, 하부 암반과의 접촉면에서는 인장 응력이 소량 감소하는 경향을 보였는데 이는 하부 기반암간의 접촉면으로 인해 미끌림이 크게 발생되지 않음을 의미한다.
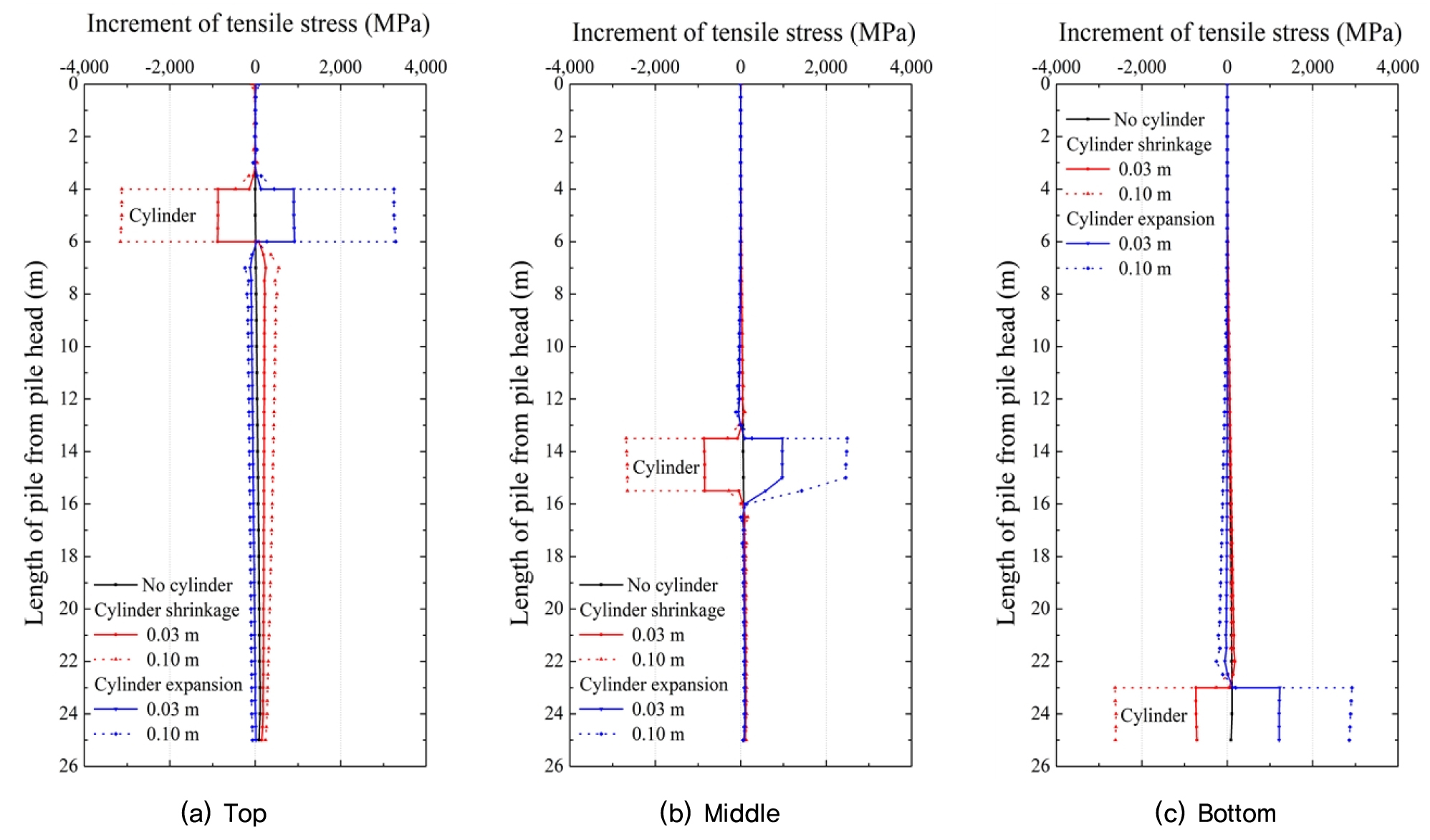
말뚝 두부에 극한 하중이 작용하고 있고 지반 융기량이 0.3m 일 때, 실린더를 각 위치(상단, 중단, 하단)에서 수축/팽창 시킨 결과는 Fig. 10과 같다. 인장 응력의 증가값에서 (+)는 인장 응력, (-)는 압축 응력을 의미한다. 공통적으로 실린더가 수축할 경우 실린더에는 압축 응력이 발생하였으며, 실린더 이외 말뚝 부분에는 인장 응력이 본래 응력보다 증가하였다. 반대로 실린더가 팽창할 경우 인장응력은 실린더에서 부담하며, 실린더 이외 말뚝 부분에는 압축 응력이 작용하였다. 실린더가 0.03m 수축하였을 경우 최대 압축 응력은 실린더 부분에서 874.5MPa 만큼 부담하며, 실린더 하단부에서 247.3MPa의 인장응력이 작용한다. 반대로 0.03m 팽창하였을 때 최대 인장 응력은 실린더 부분에서 901.6MPa 부담하며, 실린더 하단부에서 116.9MPa의 압축응력이 작용한다. 0.1m의 수축/팽창 시에는 실린더가 받는 응력이 약 4배 이상 증가하기 때문에 이는 적절하지 않은 것으로 판단되며, 지반 융기 시에는 소량의 실린더 움직임만으로도 말뚝에 작용하는 하중을 억제 할 수 있다고 보여 진다. 또한, 실린더가 팽창 할 경우 말뚝에 작용하는 인장 응력을 실린더 자체에서 부담하기 때문에 지반 융기 대응에 조금 더 적절할 것으로 예상되며, 실린더의 위치 및 팽창량에 따라 인장 및 압축 응력 값의 차이가 발생하기 때문에 지반 환경에 맞게 유연하게 적용할 필요가 있을 것으로 판단된다.
4.3 지반 침하에 따른 말뚝 거동 분석
지반 침하에 따른 말뚝의 거동은 부주면 마찰력의 발현과 이에 따른 지지력 저하와 관련이 있다고 보고되어져 왔다. 하지만 Tan and Fellenius(2016)는 수직구나 선행 재하가 되어있는 매립지에서 침하량이 상대적으로 작음을 분석하였으며, 기존 부주면 마찰력을 고려한 설계 방법은 보수적이기 때문에 이에 대한 연구를 유한요소법 수치해석으로 수행하였다. 해석 결과 부주면 마찰력은 단순히 지반과 말뚝간의 상대적인 침하에 대한 함수식이라고 정의하였으며, NCHRCP12-116(Rollins, 2019)에서도 침하에 따른 부주면 마찰력은 지반공학적인 하중(지지력 등)의 감소를 발생 시키지 않으며, 말뚝 자체의 내부적인 압축 축 강도에만 관련된다고 하였다.
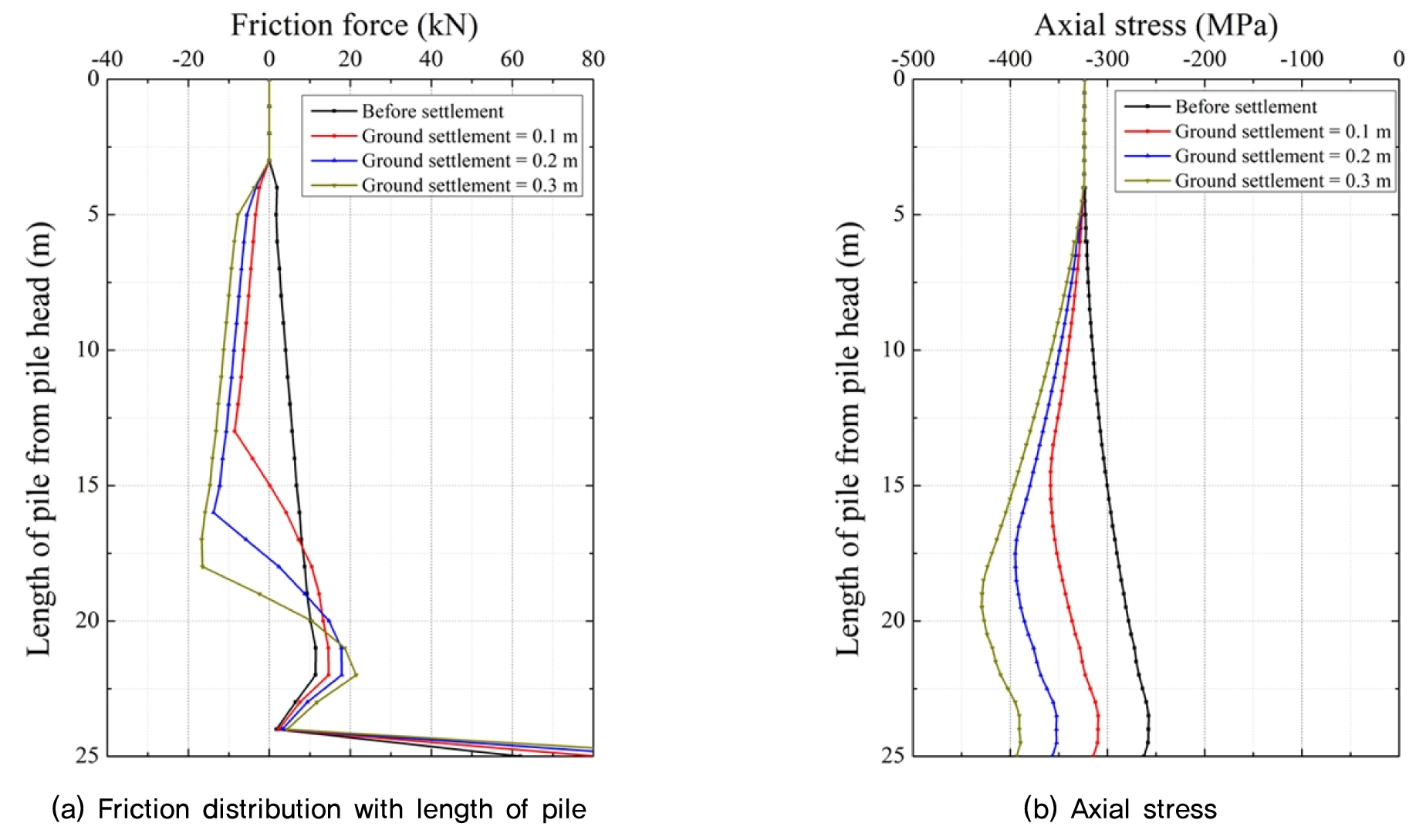
따라서 본 연구에서는 말뚝의 지지력은 변화는 고려하지 않으며, 침하에 따른 부주면 마찰력 발생과 이에 따른 축 응력을 Fig. 11과 같이 도식화하였다. 마찰력 분포에서 침하가 발생하지 않을 경우 (-)의 값은 가지지 않는 정주면 마찰력만 발현되며, 침하가 진행될수록 (-)의 값을 가지는 부주면 마찰력이 증가하고, 최대 부주면 마찰력 발생 지점이 지표면에서부터 깊게 위치하였다. 또한, 마찰력이 0이 되는 중립점의 위치도 침하량이 클수록 점차 깊게 위치함을 확인하였다. 부주면 마찰력은 말뚝과 지반 사이의 상대적인 변위 차(말뚝의 침하량보다 지반의 침하량이 클 경우)에 의해 발생되며, 중립점은 변위 차가 발생되지 않아 마찰력이 0이 되는 지점이다. 중립점의 위치는 침하에 따른 말뚝의 축 응력 변화에서도 확인 할 수 있다(Fig. 11(b)). 침하를 받지 않는 말뚝의 경우 상부 하중에 의해 압축력이 작용하나 깊이가 깊어질수록 하중 전단율이 떨어져 압축력이 감소한다. 하지만 침하 발생 시 말뚝에 작용하는 압축 응력이 증가하였고, 최대 압축응력 발생지점은 Fig. 11(a)의 마찰력이 0이 되는 중립점의 위치와 같다. 각각 0.1m 침하 시 최대 압축응력과 발생 지점 및 중립점은 다음과 같다; (1) 0.1m 침하 : 최대 압축응력 358.48MPa, 발생 지점 및 중립점 : 15.0m, (2) 0.2m 침하 : 최대 압축응력 394.93MPa, 발생 지점 및 중립점 : 17.5m, (3) 0.3m 침하 : 최대 압축응력 429.21MPa, 발생 지점 및 중립점 : 19.5m. 해석 결과를 토대로 침하에 따른 부주면 마찰력은 말뚝에 작용시키는 압축 응력을 증가시키며, 마찰력이 0이 되는 중립점에서 최대 압축응력이 발현됨을 알 수 있다.
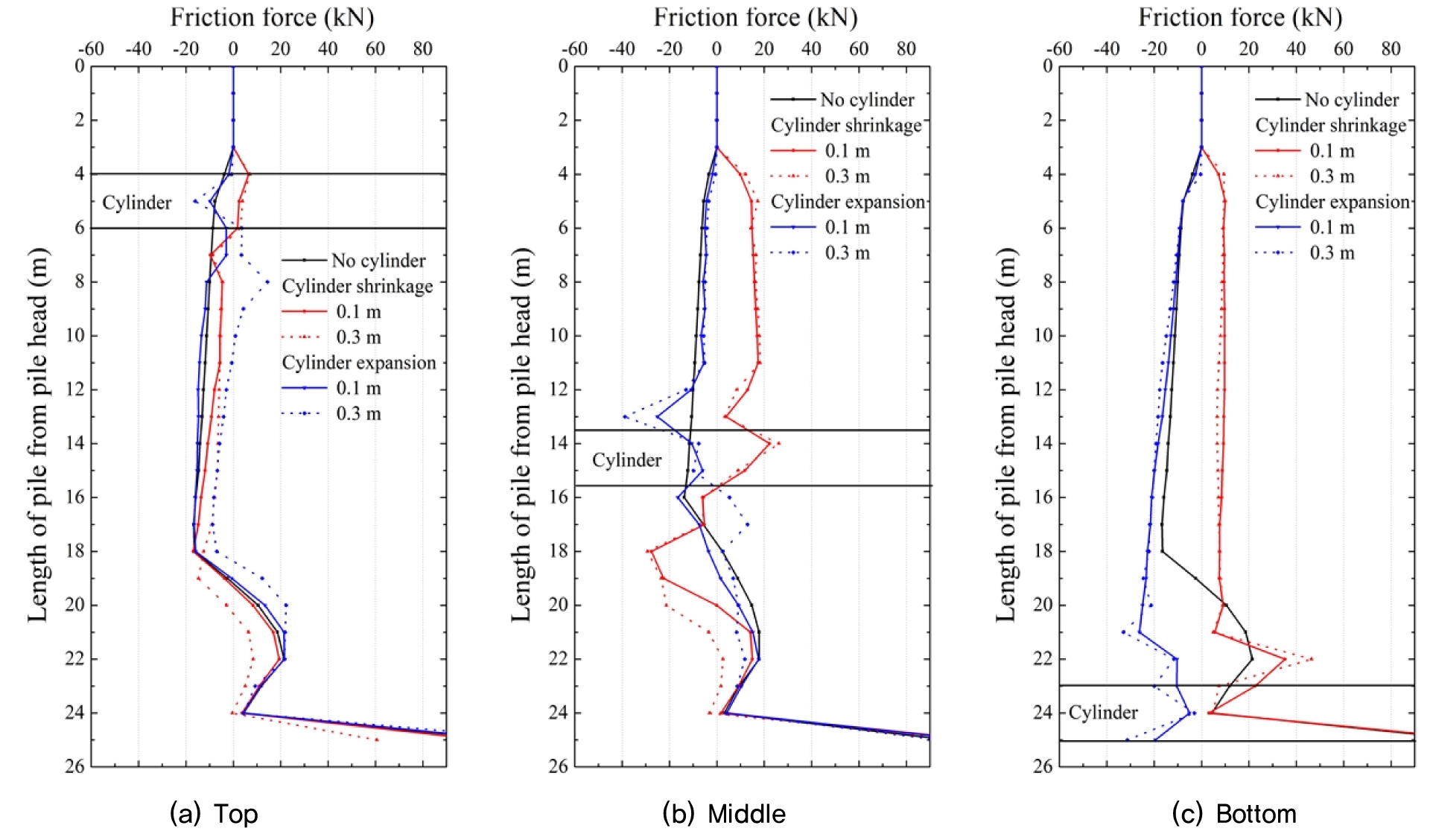
말뚝 두부에 극한 하중이 작용하고 있고 지반 침하량이 0.3m일 때, 실린더를 각 위치(상단, 중단, 하단)에서 수축/팽창 시킨 결과는 Fig. 12와 Table 2와 같다. 실린더가 최하단에 위치하고 수축량이 클 때 부주면 마찰력은 발현되지 않았으며, 마찰력이 크게 발생하였으며, 최하단 위치 및 팽창량이 클 때 부주면 마찰력만이 발생하고, 마찰력은 가장 낮게 측정되었다. 실린더가 상단 및 중단에 위치할 경우 실린더의 동작(수축/팽창) 및 부피 변화량에 따라 상이한 경향을 보였는데 이는 중립점 위치(말뚝 길이 19.3m)에 따른 영향으로 판단된다. 즉, 중립점 이상의 깊이에서 실린더가 작용하더라도 하부 깊이는 말뚝과 지반 사이의 상대적인 변위 차이가 발생하고, 실린더의 작용은 새로운 변수로 지반 내 마찰력 분포에 작용하기 때문에 정확한 경향 파악이 어렵다. 반면 실린더를 중립점 이하의 깊이에 설치할 경우 상단에 발생하는 지반과 말뚝의 상대 변위 차이를 저감시켜 준다. 따라서 침하가 발생 할 경우 지반 대응형 말뚝의 실린더는 중립점 이하의 깊이에 설치하여야 하며, 팽창은 부주면 마찰력을 보다 가속화하기 때문에 수축을 하는 것이 적합하다.
Table 2.
Friction force of pile surface according to locations and deformation of cylinder
5. 결 론
극한지 및 극서지의 지반은 기후 및 기상 등에 따라 국내 지반 조건과는 상이한 지질특성을 가지고 있으며 이로 인해 지반 변형이 발생할 수 있다. 따라서 본 연구에서는 극한지 및 극서지와 같이 지반 변형(융기, 침하 등)이 예상되는 지역에서의 능동적으로 대처 가능한 환경 대응형 말뚝 기초를 개발하고자 하며 이를 수치해석적으로 검증하였다. 해석 결과 결론은 다음과 같다.
(1) 실린더의 수축 및 팽창은 해석 프로그램 상 열팽창 모델로 모사하였다. 열팽창 변형률은 재료 자체의 물성인 탄성계수, 밀도 등에 영향을 받지 않으며 온도 변화와 계수와 관련이 있다. 모사 결과 각 계수에 따라 실린더의 팽창 및 수축이 발생하였으며, 중력이 작용하더라도 실린더의 위치에 따른 부피 변화비는 차이를 보이지 않아 해당 모델이 요소의 부피 변화만을 모사한다는 것을 검증하였다.
(2) 지반 융기는 말뚝의 인장 응력을 증가시켜 말뚝의 인장 파괴를 발생시킨다. 융기량이 0.1m 일 경우 최대 인장 응력은 42.88MPa이며, 0.2m에서는 79.47MPa, 0.3m 에서는 112.92MPa이다. 융기 시 지반 변형 대응형 말뚝의 최적 작용은 실린더의 팽창으로 판단되며, 실린더 내에서 인장 응력을 부담하며, 말뚝 부분에는 압축 응력을 유도가 가능하다. 실린더는 말뚝 상단에 위치하는 것이 인장력을 많이 부담하였는데 적절한 실린더의 위치 및 팽창량은 지반 및 말뚝의 허용 인장 강도 및 변위에 따라 결정해야 할 것으로 판단된다.
(3) 지반 침하는 말뚝의 압축 응력을 증가시키는 인자로 침하량이 증가 할수록 작용하는 압축응력은 증가하였고, 최대 압축응력은 마찰력이 0이 되는 중립점에 작용한다. 최대 압축응력은 침하가 일어나지 않았을 때를 기준으로 10.58%(0.1m 침하), 21.83%(0.2m 침하), 32.41%(0.3m 침하)가 발생하였다. 지반 대응형 말뚝으로 실린더 설치 시 실린더의 위치와 수축/팽창 거동에 따라 주면 마찰력의 발생 경향은 다양하게 나타났다. 해석 결과 지반 대응형 말뚝 적용 시 중립점 아래 위치에 실린더를 설치하고, 실린더의 수축 조건을 가해야 부주면 마찰력이 감소됨을 확인하였다. 하지만 부득이하게 중립점 깊이 이상 설치해야 하는 경우 실린더의 폭, 위치, 수축/팽창 거동 및 부피변화량을 세부적으로 설계 할 필요가 있다.
(4) 전체적으로 팽창 및 수축량은 상부 구조물의 허용 변위량 기준 내에서 결정되어야 하며, 허용 범위 내에서 실린더가 작동해야 한다. 또한, 본 연구에서는 지반 대응형 말뚝 기초 개발을 위한 선행 연구 단계로 경향 및 실현 가능성을 수치해석으로만 분석하였기 때문에 추가적인 실험적 연구가 필요하다. 이에 따라 추가적인 해석 결과를 토대로 지반 대응형 말뚝 기초의 파일럿 형식을 제작할 예정이며, 실험을 통해 보다 신뢰성 있는 데이터를 취득할 예정이다.