1. 서 론

말뚝기초의 지지력은 선단지지력과 주면마찰력으로 구분되며, 선단지지력은 기초지반의 강도에 기인하기 때문에, 지지력 예측 및 평가가 비교적 용이하다. 그러나 말뚝 주면의 전단저항으로 발휘되는 말뚝-지반 경계면의 마찰저항은 말뚝의 형상, 표면 거칠기 및 지반의 공학적 특성 등에 의존하기 때문에, 평가 및 예측에 많은 조건을 고려할 필요가 있다. 즉, 말뚝의 지지력 설계의 신뢰성을 향상시키기 위해서는 다양한 지반의 공학적 특성에 따른 말뚝-지반 경계면의 전단저항 특성을 평가해야 한다(You et al., 2018).

대표적인 말뚝-지반 경계면의 전단저항에 관한 연구는 Meyerhof and Adams(1968) 및 Meyerhof(1976)에 의한 말뚝의 인발저항이 경계면의 주면마찰력에 의존한다는 연구결과와 O’Neill and Reese(1999)이 제시한 현장타설말뚝의 인발저항 설계법이 잘 알려져 있다. 즉, 말뚝의 주면마찰력은 인발저항 설계의 중요 요소라 할 수 있다. 이에 매입말뚝의 지지력과 침하의 영향인자(Jung et al., 2017), 경사도에 따른 말뚝의 인발거동 특성(Kim, 2008), 말뚝기초의 축방향 저항효과 분석(Ma et al., 2023)에 관한 연구가 수행된 바 있다. 또한 Cho and Kim(2010)은 인발저항이 고려된 말뚝의 하중분담효과를 평가하였고, Lee(2013)는 사질토지반의 상대밀도와 구속압이 말뚝의 주면마찰력에 미치는 영향을 분석하였다. Emirler et al.(2019)과 Chen et al.(2022)은 모래의 상대밀도가 말뚝의 인발저항에 미치는 영향을 평가하였다. Dai and Wan(2018)와 Wang et al.(2023)은 직접전단시험 결과를 이용하여 그라우팅이 pile-soil interface과 말뚝기초 주변 지반의 전단강도 향상에 미치는 영향을 분석한 바 있다. Ashour and Abbas(2020)은 다층지반에 설치된 인발저항 말뚝에 대하여 말뚝-지반 경계면의 마찰저항에 대한 하중 전달 메커니즘을 연구하였고, Tovar-Valencia et al.(2018)은 디지털 이미지를 통해 모래 지반에 다른 표면 거칠기를 갖는 모델 말뚝의 인장 특성을 평가한 바 있다. 이와 같이, 말뚝의 주면마찰력과 인발저항에 관한 실험 및 해석 연구가 다양하게 수행되었다.

말뚝의 인발저항에 관한 정량적 평가는 실험 또는 수치해석을 통해 이루어지는데, 지중에 시공되는 말뚝은 실제 구속압의 영향을 받게 된다. 즉, 말뚝-지반 경계면의 전단저항 평가를 위해서는 구속압의 크기를 고려할 필요가 있다. 특히, 수치해석을 이용한 말뚝-지반 경계면의 전단저항에 대하여 보다 엄밀한 분석을 위해서는 지중 구속압과 경계면 저항의 상관성 평가가 요구된다. 따라서 본 연구에서는 지중 구속압을 고려한 말뚝-지반 경계면의 전단거동에 관한 유한요소해석을 수행하였다. 그리고 구속압과 말뚝-지반 경계면 전단 특성의 관계를 평가하기 위하여 강도감소계수가 적용된 해석 결과를 실험결과와 비교ㆍ분석하였다.

2. 말뚝 인발 모형실험

말뚝에 작용하는 지중 구속압과 말뚝-지반 경계면 전단거동의 관계를 평가하기 위해서 유한요소해석을 실시하였다. 그리고 유한요소해석 결과의 검증을 위해 지반의 세립분 함유율과 말뚝에 작용하는 구속압이 말뚝 인발에 미치는 영향을 평가한 기존 연구(You and Hong, 2023)와 비교하였다.

2.1 실험 개요

You and Hong(2023)은 세립분 함유율에 따른 모형 지반을 조성하여 구속압에 따른 모형 말뚝의 인발에 관한 실험을 수행한 바 있다(Fig. 1). 그리고 실험결과를 이용하여 지반의 세립분 함유율(0%, 5%, 7%, 10%, 15%, 20%) 조건을 고려한 말뚝-지반 경계면에서의 인발저항 성능을 평가하고자 하였다. 실험 방법 및 내용을 요약하면 다음과 같다.

Fig. 1.

Concept of pullout model test (You and Hong, 2023)

모형 지반의 세립분 함유율은 주문진 표준사에 대한 세립토의 중량비로 적용하였으며, 모형 말뚝은 말뚝의 거친 표면을 일정하게 모사하기 위해서 강봉의 표면에 사포(sandpaper, #40)를 균일하게 부착하였다. Fig. 1(a)과 같이, 말뚝에 작용하는 구속압은 모형 지반 상부에 말뚝을 제외한 중공의 원형 재하판으로 상재하중을 가압하였고, 수평토압은 정지토압계수(K₀=1-sinφ)를 이용하여 산정하였다(Fig. 1(b)). 세부적인 실험 방법 및 내용은 기존 연구(You and Hong, 2023)를 통해 참조할 수 있으며, 실험 케이스는 Table 1에서 보는 바와 같다.

2.2 실험 결과

Fig. 2는 말뚝 인발 모형실험 결과를 인용한 것으로, 세립분 함유율의 변화와 구속압의 크기에 따른 말뚝의 최대 인발저항력을 확인할 수 있다. 최대 인발저항력은 말뚝에 작용하는 구속압이 증가할수록 증가하였으며, 구속압에 관계없이 세립분 함유율이 증가할수록 최대 인발저항력은 감소하는 경향을 보였다. 또한 구속압이 증가할수록 세립분 함유율의 낮은 경우에는 최대 인발저항력의 차이가 크게 나타났지만, 세립분 함유율의 높은 경우에는 최대 인발저항력의 차이가 상대적으로 크지 않음을 알 수 있었다.

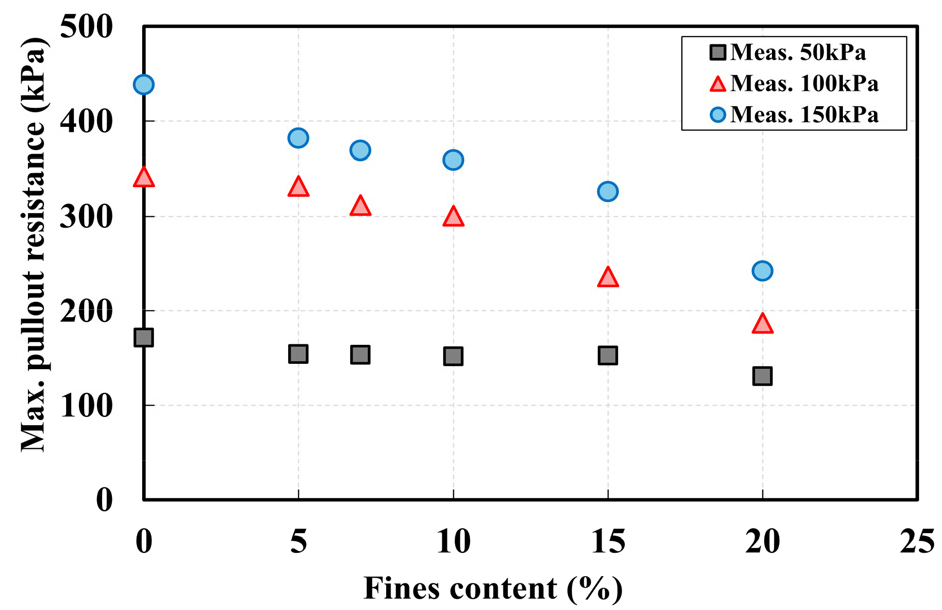
Fig. 2.

Maximum pullout resistance of pile (You and Hong, 2023)

3. 말뚝 인발 모형실험에 대한 유한요소해석

3.1 해석 방법 및 내용

전술한 말뚝 인발 모형실험을 모사하기 위한 유한요소해석은 범용 프로그램인 GTS NX를 이용하였으며, 그 결과를 실험 결과와 비교하였다.

먼저, 말뚝 표면의 거칠기와 말뚝에 작용하는 구속압에 따른 말뚝-지반 경계면의 전단저항을 고려할 수 있도록 경계면 강도 감소계수(R)의 산정을 위한 인터페이스 요소를 적용하였다. 그리고 말뚝의 인발은 강제 변위를 통해 제어하였으며, 원통형 모형실험을 모사하기 위해 축대칭 해석을 실시하였다. 또한 기존 연구(You et al., 2019a)를 참고하여 말뚝 선단부 요소의 영향을 최소화하기 위한 가상 지반을 가정하여 적용하였고, 해석모델은 Fig. 3에서 보는 바와 같다. 이를 통해 해석 결과를 검증하기 위해 강도감소계수에 따른 해석 결과(최대 인발저항력)를 실험 결과에서 도출된 최대 인발저항력과 비교·분석하였다.

Fig. 3.

FEA model in applied axisymmetric analysis

지반의 점착력과 내부마찰각은 기존 연구(You et al., 2019b)를 통해 적용하였으며, 지반 변형계수 및 포아송비는 Table 2와 같이 적용하였다. 지반 변형계수는 세립에 대하여 Hunt(1986)가 제시한 지반 특성을 고려하였으며, 포아송비는 Das and Sobhan(2013)의 제안범위에서 세립분 함유율에 따라 적용하였다. Fig. 4는 말뚝의 인발저항이 지반의 변형특성에 따라 상이하기 때문에, 지반 변형계수(E₅₀, E_oed, E_ur)를 세립분 함유율에 따라 나타낸 것이다.

Fig. 4.

Deformation modulus according to fines content

해석모델의 지반은 탄소성 거동을 표현할 수 있는 Hardening soil 모델(Schanz et al., 1999)을 적용하였으며, 이는 기존 연구(Hong et al., 2019)에서 Mohr-Coulomb 모델과 Hardening Soil 모델을 이용한 말뚝 인발 거동 평가를 통해 Hardening soil 모델의 적용이 보다 합리적인 것으로 평가된 결과를 참조하였다.

Hardening soil 모델에서는 축변형률(ε₁)과 축차응력(q)는 다음 식 (1)과 같은 관계로 표현되며, q_a는 수렴 축차응력을 의미한다.

Fig. 5는 식 (1)을 응력-변형률 관계로 나타낸 그림이며, 하중 증가(loading)에 따른 E₅₀과 재하중(reloading) 또는 제하중(unloading)에 대한 E_ur은 각각 다음 식 (2) 및 식 (3)과 같다.

E₅₀^ref은 하중 증가시 기준 구속압 σ^ref에 대응하는 기준 탄성계수이며, m은 구속압에 대한 계수로 일반적인 적용값 0.5를 사용하였다. 그리고 E_ur^ref는 재하 또는 제하 시 기준 구속압 σ^ref에 대응하는 기준탄성계수로 일반적으로 E₅₀^ref의 3배값을 적용하기 때문에, Fig. 4와 같이 동일한 조건으로 적용하였다.

Fig. 5.

Relationship of stress-strain in hardening soil model (Schanz et al., 1999)

Hardening soil 모델에서는 삼축응력 상태에서의 두 가지 경화함수를 정의하고 있는데, 다음 식 (4)는 전단경화, 식 (5)는 압축경화를 의미한다.

여기서, E_i는 초기 탄성계수, γ_ps는 유효소성변형률, α는 캡형상계수, P_p는 선행압밀응력을 의미한다.

압축경화에서의 q는 다음 식 (6)과 같이 표현된다.

말뚝과 지반의 경계면을 나타내는 경계면 강도감소계수(R)은 다음 식 (7)과 같이 나타난다.

여기서, G_i는 말뚝-지반 경계면의 전단탄성계수, G_soil는 지반의 전단탄성계수를 의미한다. 여기서 G_i에 사용되는 포아송비는 0.45이다.

인터페이스의 강성에 매개변수인 수직강성계수(K_n)과 법선방향 부착·탈부착 거동 탄성계수(K_t)은 다음 식 (8)과 식 (9)과 같이 구성되어 있다.

t_V는 인터페이스 요소의 가상두께를 의미하며, E_oed,i는 말뚝-지반 경계면 요소의 오이도미터 탄성계수를 의미한다.

본 연구에서 수행한 유한요소해석의 Case는 Table의 인발모형실험과 동일하며, 해석 모델과 재료정수를 요약하면 각각 Fig. 3 및 Table 3에서 보는 바와 같다.

3.2 결과 및 분석

Fig. 6은 세립분 함유율에 따라 구속압 조건에서의 말뚝 인발에 대한 응력-변형률 곡선을 나타낸 것이다. 구속압에 따른 말뚝 인발저항력의 초기 기울기는 유사한 거의 거동을 보였고, 구속압이 증가할수록 인발저항력이 증가하면서 더 높은 변형률에서 극한 인발저항이 발생하는 것을 확인하였다. 말뚝의 극한 인발저항은 기울기가 변하는 지점에서 탄성에서 소성의 영역으로 전환된다고 가정하여 설정하였으며, 극한 인발저항을 최대 인발저항력으로 정의하였다.

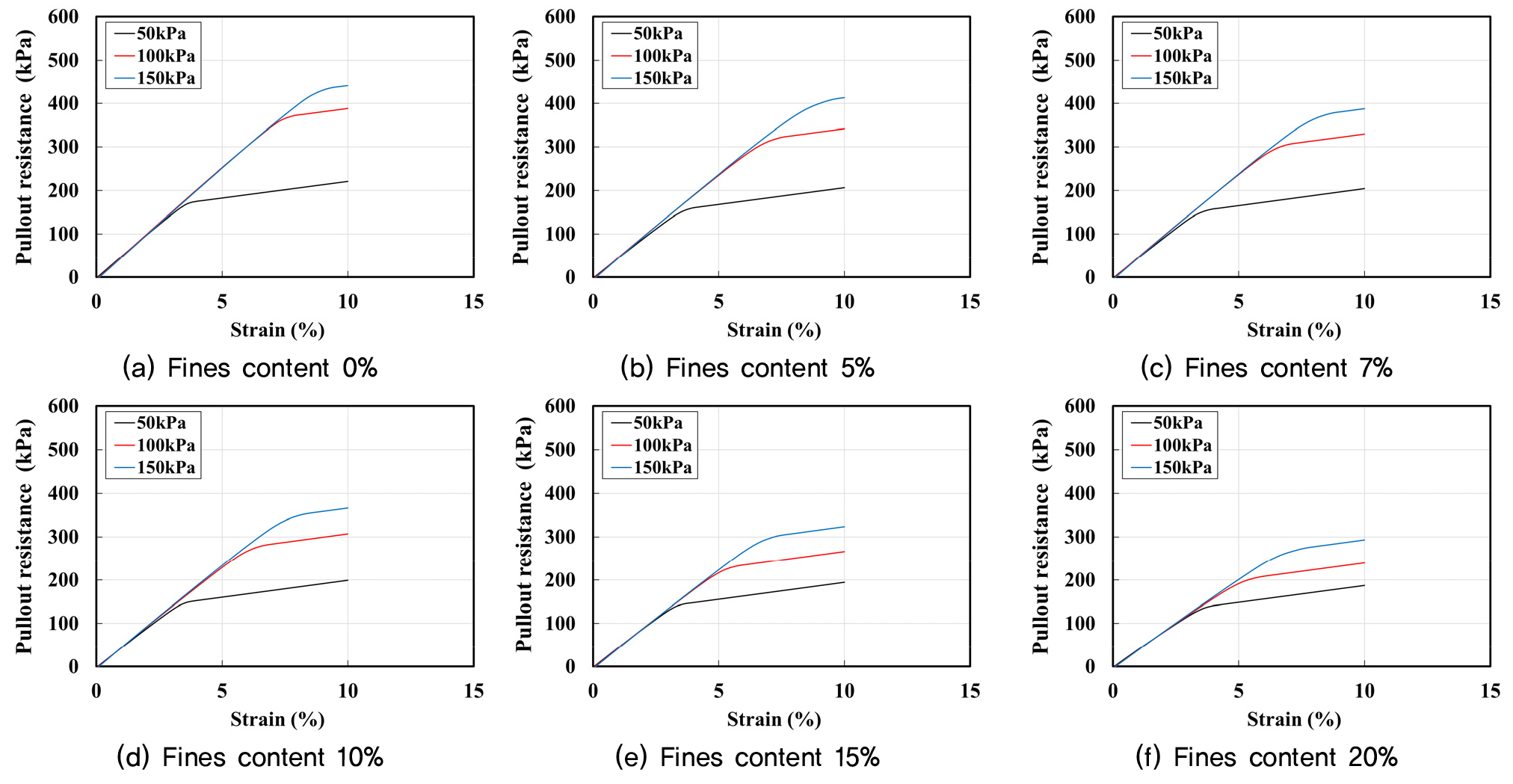
Fig. 6.

FEA Results (stress-strain curve)

Fig. 7은 해석결과로부터 산정된 최대 인발저항력을 이용하여 기존 실험 결과에 의한 최대 인발저항력과 비교한 것이다.

먼저, 낮은 세립분 함유율 조건에서 구속압이 50kPa에서 100kPa로 증가하는 경우, 최대 인발저항력의 증가 폭이 매우 컸지만, 구속압이 100kPa에서 150kPa로 증가하는 경우에는 최대 인발저항력의 증가율이 상대적으로 작았다. 그리고 세립분 함유율이 증가할수록 구속압 크기에 따른 최대 인발저항력의 증가율이 유사해지는 것을 알 수 있었다. 즉, 세립분 함유율이 증가할수록 구속압의 영향이 낮아지면서 최대 인발저항력 또한 감소함을 확인하였다. 이와 같은 경향은 실험 및 해석 결과 모두 유사하였으며, 이는 본 연구에서 수행한 유한요소해석이 기존의 말뚝 인발 모형실험을 적절히 모사한 것을 의미한다.

Fig. 8은 세립분 함유율에 따른 각 해석 조건에서 적용된 경계면 강도감소계수(R)의 변화를 도식화한 것이다. 구속압 50kPa의 경우, 세립분 함유율이 증가할수록 경계면 강도감소계수(R)의 증가가 확연하게 나타났지만, 구속압이 100kPa 및 150kPa의 경우에는 그 증가폭이 상대적으로 작은 것을 알 수 있었다. 이를 바탕으로 해석에 적용된 경계면 강도감소계수의 범위는 0.53~0.64 사이에서 결정될 수 있음을 확인하였다.

Fig. 7.

Comparison of predicted and measured maximum pullout resistance

Fig. 8.

Interface strength reduction factor(R) according to fines content

4. 결 론

본 연구에서는 지중 구속압과 말뚝-지반 경계면의 전단거동의 상관성을 평가하기 위하여 경계면 강도감소계수가 적용된 유한요소해석을 수행하였다. 그리고 해석 결과를 기존 연구 결과와 비교하였으며, 요약하면 다음과 같다.

(1)유한요소해석에 의한 응력-변형률 곡선을 평가한 결과, 구속압에 따른 말뚝 인발저항력의 초기 기울기는 유사하였지만, 말뚝 인발 시 탄성에서 소성 영역으로 전환되는 변곡점을 통해 구속압의 증가에 따라 최대 인발저항력과 함께 변형률이 증가하는 것을 확인하였다.

(2)해석 결과에서 정의된 최대 인발저항력의 경향은 실험 결과와 유사한 것을 확인하였으며, 이를 바탕으로 해석에 적용된 인터페이스 및 지반 모델과 가상 지반은 적절하게 모사된 것으로 평가되었다.

(3)기존의 실험 결과에서 구속압 및 세립분 함유율 증가에 따라 최대 인발저항력의 증가율이 감소하는 경향을 모사하기 위한 경계면 강도감소계수의 적용은 구속압과 세립분 함유율이 고려되어야 하는 것으로 분석되었다.