1. 서 론
도로 건설 프로젝트는 국토 균형 발전과 더불어 경제 성장과 사회 발전을 위한 필수적인 공공사업 이다. 현행 공공사업에서 가장 중요한 요소 중 하나는 정확한 근거와 합리적인 방법을 통해 계획을 수립하고 그에 따른 예산을 책정하여 계약을 체결하는 것이다. 그러나 최근 공공사업의 규모가 확장되며 도로 건설은 다양한 요소들이 상호작용하는 특수성을 보임에 따라 건설비 예측에 대한 불확실성으로 인한 문제가 발생하고 있다(Park, 2011).
도로 건설비 산출에는 지형 조건, 기후, 인건비 등 다양한 요소들이 영향을 미치며 이러한 변수들의 불확실성 및 복잡성으로 인해 초기 계획단계에서의 건설비가 실제 건설비와 차이를 보이게 되며 이는 도로 건설 프로젝트의 시간적, 경제적 손실로 이어지게 되므로 합리적인 방법을 통한 건설비 예측이 중요하다. 하지만 기존의 건설비 예측은 도로 업무편람(MOLIT, 2013)과 같은 개략건설비의 기준을 따르고 있어 실제 건설비로 예측되기에 정확성에서의 문제점을 갖고 있다. 이와 같은 문제를 해결하기 위해 비선형 통계적 학습을 통해 예측값을 산출하는 인공신경망(Artificial Neural Network, ANN)을 통한 예측 방법이 최근 몇 년간 많은 분야에서 사용되고 있다(Oh et al., 2022).
관련 연구들을 살펴보면, 국외의 경우 Gunaydin and Dogan(2004)은 건설 설계 초기 단계에서 30건의 실제 데이터를 활용하여 주거용 빌딩의 면적당 공사비를 추정하였으며, Petroutsatou et al.(2012)은 터널의 공사비를 추정하기 위해 33건의 실제 데이터를 활용하여 인공신경망 모델을 구축하였으며, Elbeltagi et al.(2014)은 고속도로 개략 공사비 추정을 위해 67건의 실제 데이터를 활용하여 인공신경망 모델을 구축하였다. 국내의 경우 Han et al. (2011)은 도로공사의 개략공사비 추정을 위해 공사비와 상관성이 높은 입력변수 선정 후 인공신경망 모델을 구축하였으며, Park et al.(2010)은 속성 가중치 산정을 중심으로 사례기반 추론을 활용하여 초기단계에서의 공사비 예측 방법을 제시하였다. 또한 Lee(2011)는 초기 공사비 예측에 있어 PSO 알고리즘을 활용하여 최소한의 사업정보를 가지고 건설사업에서의 공사비 예측 모델을 제시하였다.
본 연구에서는 도로 건설비용 예측을 위해 도로 총연장, 도로 폭, 공사 기간, 터널 연장, 교량 연장, 설계 속도 등 도로 건설 프로젝트와 직접적으로 연관된 6개의 구체적인 설계 변수를 종합적으로 활용했다. 이는 기존 연구들이 특정 설계 변수나 환경 요소에 국한된 반면 본 연구에서는 건설비용과 직접적으로 연관된 핵심 변수들을 종합적으로 고려하였다는 차별점이 있다. 더불어, 본 연구는 도로 건설비용이라는 특정 문제를 해결하기 위해 인공신경망(Artificial Neural Network, ANN)을 최적화된 형태로 적용하여, 기존 연구가 일반적인 토목 공사비용이나 개별 구조물의 비용 추정에 집중한 것과 달리 본 연구는 도로라는 인프라의 특수성에 맞춘 맞춤형 분석을 통해 초기 계획 단계에서 예측 정확도를 높이고 비용 초과를 사전에 방지하며, 프로젝트 관리의 효율성을 극대화하는 데 기여하고자 하였다.
2. 연구 방법
본 연구에서는 도로공사 계획단계에서 활용 가능한 건설비 예측 모델 개발을 위해 총 74개의 일반국도 건설 공사 자료를 활용하였다.
예측된 모델을 통한 결과값을 도로업무편람(MOLIT, 2013)의 도로건설 단가와 비교하여 인공신경망을 활용한 도로건설비 예측에 대한 검증을 수행하였다.
2.1 입력 자료
2.1.1 자료 수집
인공신경망 모델 설계를 위해 도로 총연장, 설계속도, 공사 기간, 도로의 폭 등을 입력 변수로 설정 후 건설 비용을 출력 변수로 설계하였으며, 입력변수가 도로 건설 비용에 미치는 영향을 분석하였다. 학습을 위해 추출된 입력 변수들의 분포는 Table 1과 같다.
Table 1.
Distribution of input factors
2.1.2 자료의 정규화
인공신경망 학습 과정에서의 수치적 안정성을 위해 본 연구에서 사용된 총 74개의 데이터를 식 (1)과 같이 정규화 하였다. 이는 보다 효과적인 신경망 학습을 위해 수행하는 자료의 선처리 과정으로 데이터는 0과 1사이의 값으로 변환된다.
여기서, : 정규화 값
: 입력 변수의 값
: 입력 변수의 최대값
: 입력 변수의 최소값
2.2 인공신경망 모델 설계
2.2.1 자료 구분
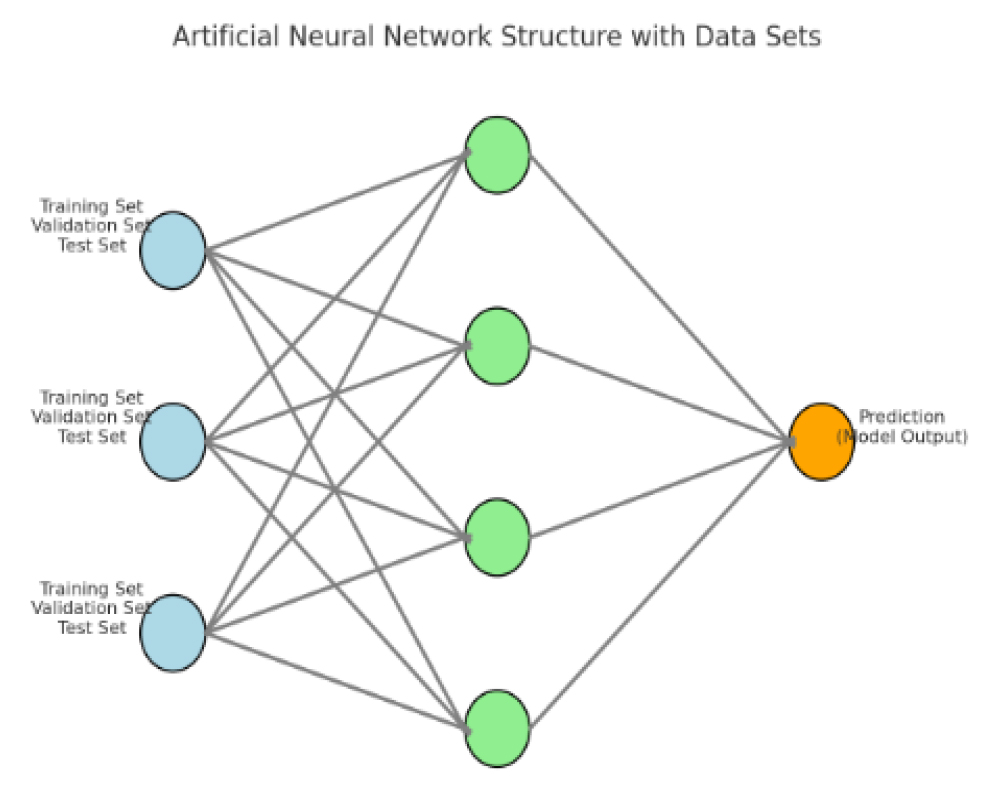
인공신경망 모델의 예측을 위해서는 학습세트(Training set)와 시험세트(Test set) 등 두 개의 세트로 나누어 전체 데이터를 사용하지만 이 경우 학습된 모델에만 적합한 과적합(Overfitting)이 발생할 가능성이 높아져 검증단계를 필요로 하게 된다. 따라서 본 연구에서는 Fig. 1과 같이 훈련세트, 시험세트 외에 검증세트(Validation set) 총 3개의 세트로 전체 데이터를 구분하여 모델을 설계하였다.
2.2.2 모델 설계
본 연구에서는 도로 총연장, 도로 폭, 공사 기간, 터널 연장, 교량 연장, 설계 속도 6개의 입력변수를 사용하였으며, 출력층은 도로 건설비용으로 결정하였다. 모멘텀은 이전 학습 단계에서의 가중치 변경분을 일정 비율로 현재 변경분에 반영하여, 학습 과정에서 발생할 수 있는 진동을 줄이고 더 빠른 수렴을 가능하게 한다. 이를 통해 네트워크는 지역 최소값(local minima)에 덜 갇히며, 전역 최소값(global minimum)을 향해 보다 효율적으로 이동할 수 있다. 학습율은 각 학습 단계에서 네트워크의 가중치가 얼마나 조정될지를 결정하며, 적절한 학습율 설정은 네트워크가 학습 데이터에 과도하게 반응하여 과적합(overfitting)이 발생하거나, 반대로 반응이 너무 느려 수렴하지 못하는 문제를 방지한다. 이 연구에서는 최적의 인공신경망 입력 조건을 도출하기 위해 모멘텀 계수, 뉴런수, 활성화 함수 조건, 은닉층수를 달리하며 학습 후 상관 계수(Correlation coefficient, r) 비교를 통해 검토하였다. 최적 입력조건을 바탕으로 오차가 가장 적은 인공신경망 모델을 결정하기 위해 총 10개의 모델에 대한 성능평가를 실시하여 RMSE(Root Mean Square Error) 값과 상관계수 값을 비교 분석하였다.
2.2.3 모델 학습 단계
본 연구에서는 일반적인 인공신경망 학습에 널리 사용되는 전진형 역전파(Feed-forward backpropagation) 알고리즘을 사용하였다. 이는 네트워크 에러 함수를 최소화하여 최적의 연결강도 값을 찾는 알고리즘이다(Hwang, 2005).
활성화 함수(activation function)는 결합함수의 결과를 해석해서 출력값을 결정하는 역할을 하며, 활성화 함수가 달라짐에 따라 출력값의 변화가 발생한다. 본 연구에서는 로그 시그모이드함수(LOGSIG), 탄젠트 시그모이드함수(TANSIG), 선형함수(PURELIN)를 사용하였으며, 각 활성화 함수 별 학습 후 예측 값을 실제 도로 건설 비용과 비교를 통해 신경망 적용에 적합한 활성화 함수를 선택하였다.
또한 인공신경망 조건에 사용되는 최적의 조건을 알아내기 위해 모멘텀(Momentum)과 학습율(Learning rate)을 0.1부터 0.9까지 변화시켜 학습시킨 후, 모델을 통한 예측 값과, 실제 건설 비용 결과값의 상관관계를 이용하여 최적의 해석조건을 결정하였다. 모델에 사용된 조건은 Table 2와 같다.
Table 2.
ANN training conditions
2.2.4 모델 검증
학습된 인공신경망 모델의 결과 값이 올바른지 판단하기 위해 총 74개의 데이터 중 학습에 사용되지 않은 임의의 일반도로 10개의 데이터를 통해 모델을 검증하였다. 검증을 위해 상관계수를 활용하였으며, 식 (2)와 같이 평균제곱오차(Mean square error, RMSE) 값을 활용하여 검증의 신뢰도를 높였다.
여기서, : 평균제곱근 오차
: 실제 값
: 예측 값
: 입력 값의 수
3. 연구 결과
3.1 해석 결과
3.1.1 모멘텀 및 학습율
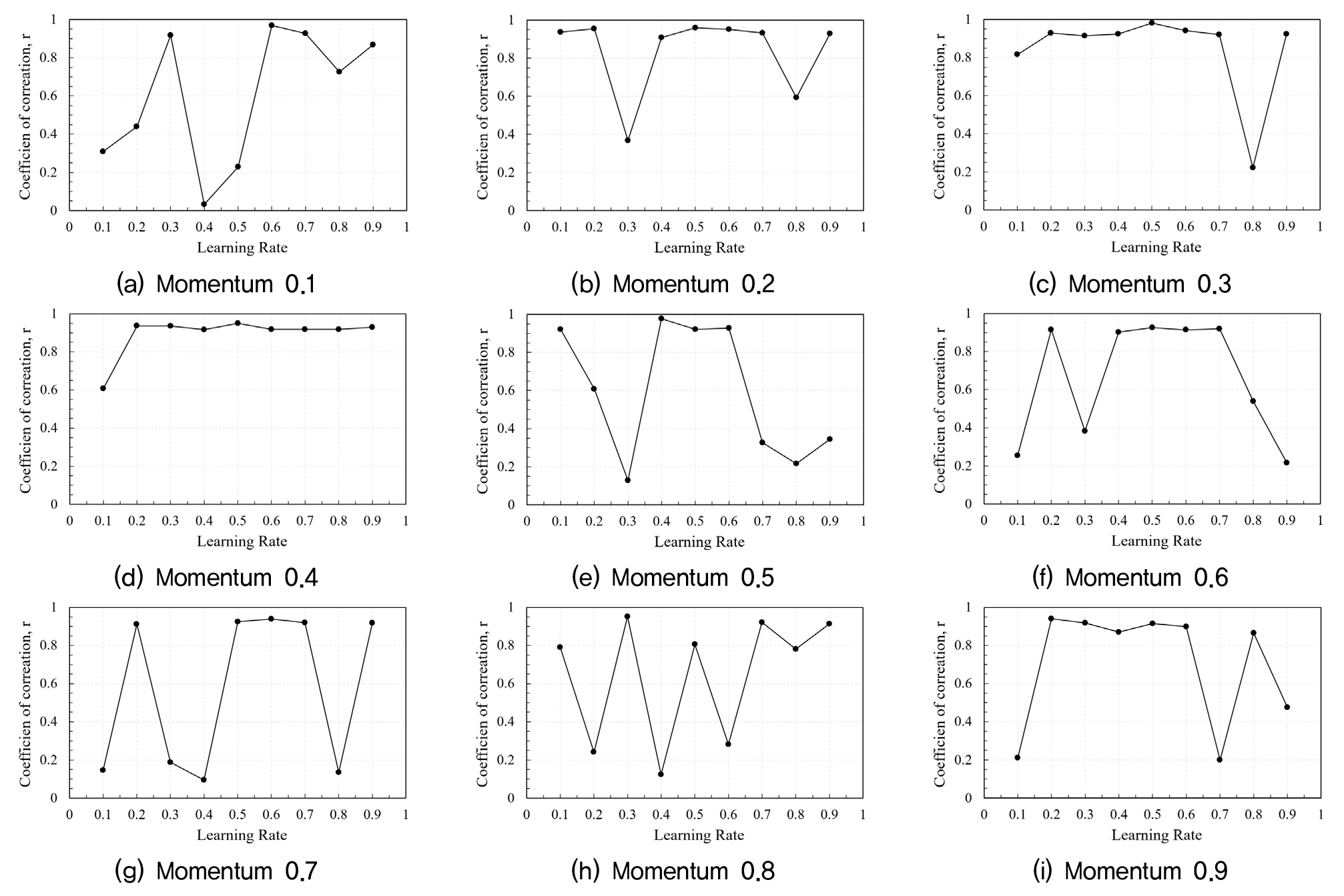
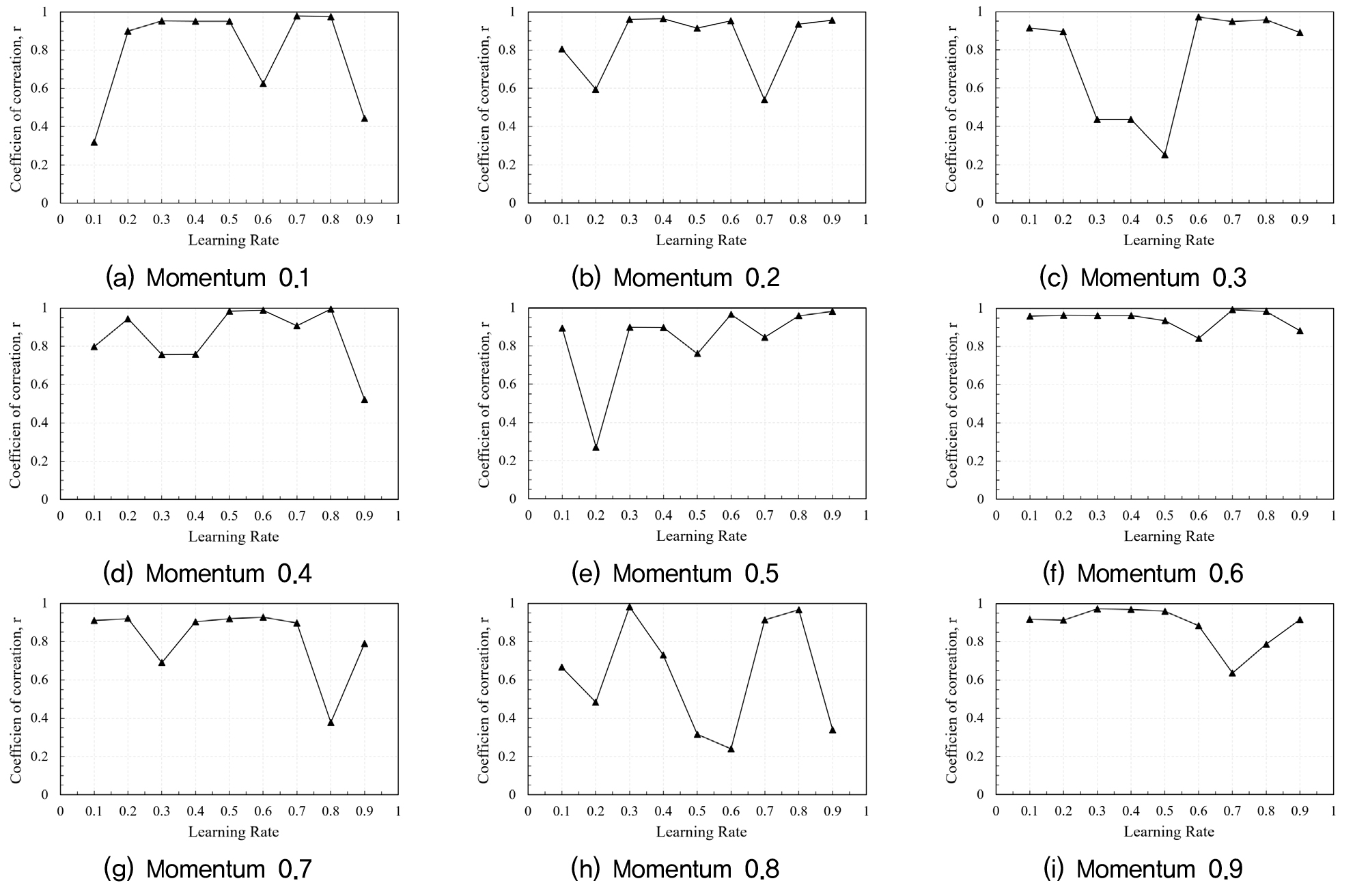
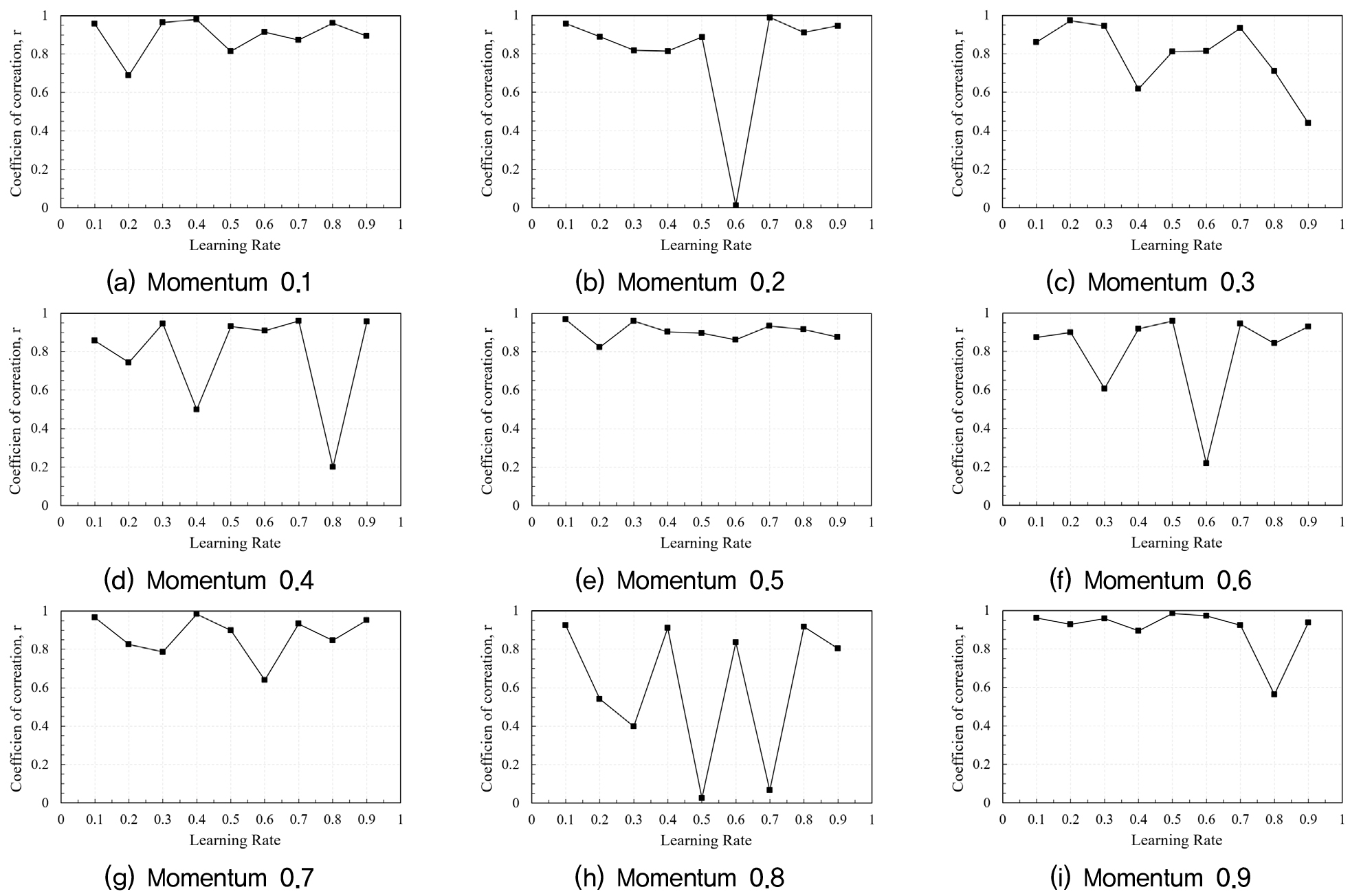
입력변수를 바탕으로 모멘텀 값과 학습율을 변화시켜 각각의 활성화 함수에 대한 영향을 분석하였다. Fig. 2, Fig. 3, Fig. 4는 각각의 활성화 함수 별 모멘텀 학습율 변화에 따른 결과값과 실제 도로 건설 비용 값과의 상관계수를 나타낸다. 또한, 활성화 함수별 상관계수 결과는 Table 3과 같다.
분석 결과에 따르면, TANSIG 활성화 함수 조건에서 모멘텀, 학습율이 각각 0.6, 0.7일 경우 상관계수가 0.9895로 가장 높게 나타났다. 이는 TANSIG는 비선형 데이터를 처리하는데 유리하지만, PURELIN의 경우 높은 모멘텀이 불필요한 선형 특성으로 인해 모멘텀 값이 낮게 나온 것으로 판단된다.
Table 3.
Decision of optimized momentum-learnig rate
| Transfer function | Momentum | Learning rate | Coefficient of correlation, r |
| LOGSIG | 0.3 | 0.5 | 0.9793 |
| TANSIG | 0.6 | 0.7 | 0.9895 |
| PURELIN | 0.2 | 0.7 | 0.9896 |
3.1.2 뉴런수
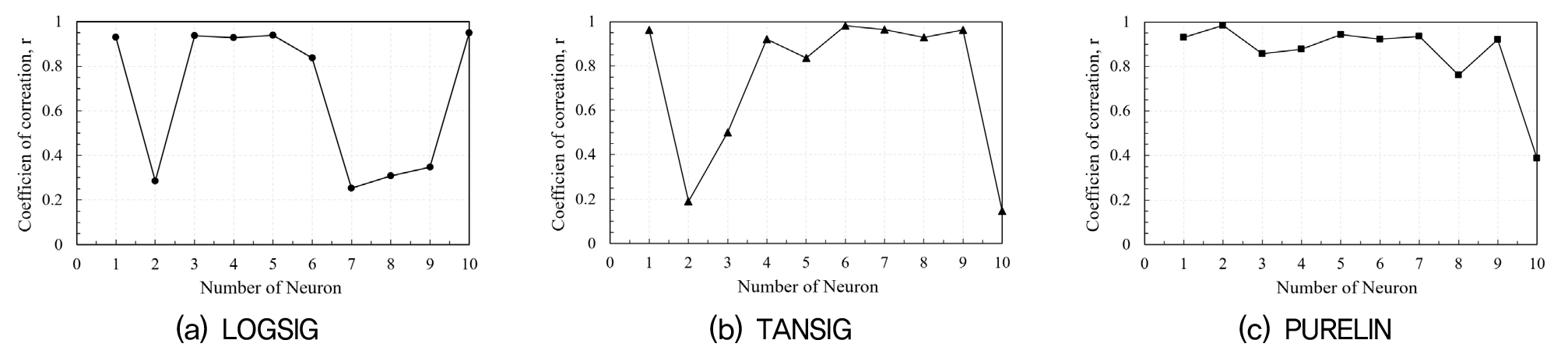
본 연구에서는 최적의 뉴런수를 찾기 위해 뉴런수를 1~10개로 조절한 뒤 예측 값에 따른 실제 건설 비용과의 상관계수를 분석한 결과는 Fig. 5와 같으며 각 활성화 함수별 최적의 조건일 때의 상관계수를 나타낸 결과는 Table 4와 같다.
각 활성화 함수별 결과 LOGSIG함수의 경우 뉴런수 10개, TANSIG의 경우 뉴런수 6개, PURELIN의 경우 뉴런수 2개일 때 각각 상관계수 0.9492, 0.9803, 0.9841로 나타났다.
Table 4.
Decision of optimized number of neurons
| Transfer function | Momentum | Learning rate | Number of neurons | Coefficient of correlation, r |
| LOGSIG | 0.3 | 0.5 | 10 | 0.9492 |
| TANSIG | 0.6 | 0.7 | 6 | 0.9803 |
| PURELIN | 0.2 | 0.7 | 2 | 0.9841 |
3.1.3 은닉층수
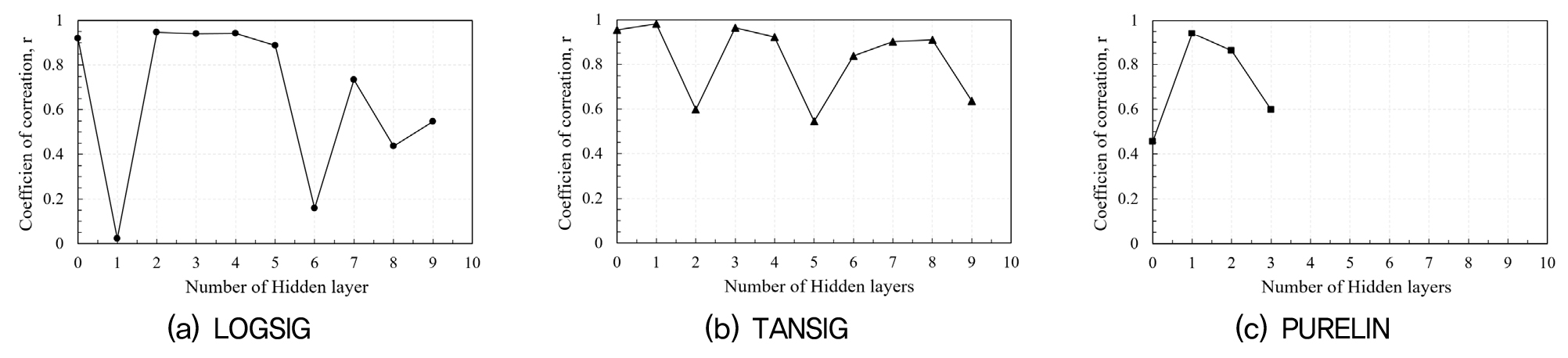
LOGSIG 함수와 TANSIG 함수의 경우 은닉층 수를 0개에서 9개로 변화시키며 예측값에 따른 실제 건설 비용과의 상관 계수 변화를 나타낼 수 있었지만, PURELIN 함수의 경우 은닉층수 5개 이상일 경우 과적합으로 인하여 결과값이 수렴하지 않는 결과를 나타내었다. 각 활성화 함수별 결과값은 Fig. 6과 같으며 최적의 조건에 따른 상관계수 값은 Table 5와 같다.
분석 결과 TANSIG 함수를 활용하여, 모멘텀 0.6, 학습율 0.7, 뉴런수 6, 은닉층수 1개를 적용한 인공신경망 모델의 경우 예측값과 실제 건설비용의 상관계수가 0.9807로 나타나 가장 예측의 정확도가 높은 입력변수 조건으로 판단된다.
Table 5.
Decision of optimized number of hidden layers
| Transfer function | Momentum | Learning rate | Number of neurons |
Number of hidden layers |
Coefficient of correlation, r |
| LOGSIG | 0.3 | 0.5 | 10 | 2 | 0.9411 |
| TANSIG | 0.6 | 0.7 | 6 | 1 | 0.9807 |
| PURELIN | 0.2 | 0.7 | 2 | 1 | 0.9370 |
3.1.4 최적 모델 결정
본 연구에서 사용된 총 6개의 입력자료를 활용하여 최적 인공신경망 모델 도출을 위한 10종류의 모델을 구성한 결과는 Table 6과 같다.
Table 6의 입력변수조건을 바탕으로 총 10개의 모델의 예측값과 실제 도로 건설비용의 상관계수(Correlation coefficient, r) 및 RMSE 값을 비교하였으며, 총 100회에 걸친 학습결과의 상관 계수 및 RMSE 분포는 Table 7과 같다.
Table 8은 각 모델별 인공신경망의 예측값과 실제 도로 건설 비용과의 정확도 검증 결과를 나타낸 것이다.
분석 결과 Model 7의 경우 상관계수 0.964, RMSE 0.033으로 다른 모델에 비해 실제 건설 비용 예측에 효율적인 모델인 것으로 판단된다.
Table 6.
Model Structure of ANN
Table 7.
Distribution of r and RMSE
Table 8.
RMSE and r Results of ANN model
| Model | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| r | 0.893 | 0.501 | 0.665 | 0.965 | 0.762 | 0.929 | 0.964 | 0.920 | 0.906 | 0.915 |
| RMSE | 0.048 | 0.084 | 0.076 | 0.044 | 0.065 | 0.064 | 0.033 | 0.064 | 0.059 | 0.051 |
3.2 기존 연구와의 비교 및 결과
3.2.1 인공신경망 모델 검증
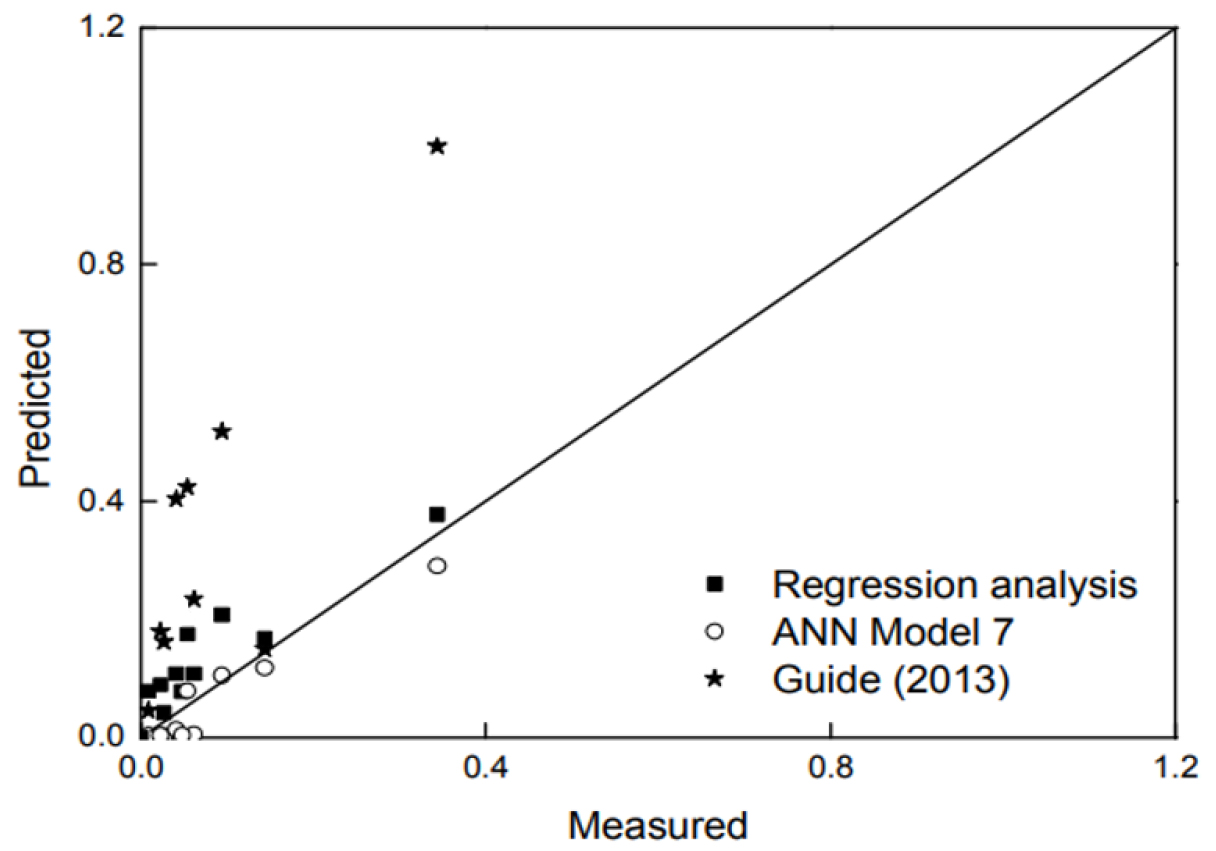
본 연구 결과 최적의 예측 모델인 Model 7과 도로업무편람의 평균단가산정방식, 회귀식을 비교하여 검증한 결과는 Fig. 7과 같다.
Table 9는 인공신경망 모델 검증을 위한 회귀식, Model 7, 도로업무편람산정방식을 비교한 값으로, 연구 결과 Model 7은 상관계수 0.964, RMSE 0.033으로 가장 높은 값을 나타내 도로 건설 비용 예측에 있어 더 정확한 모델임을 확인하였다.
Table 10은 실제 도로건설이 이루어진 10곳의 데이터를 바탕으로 인공신경망을 통한 예측값과 도로업무편람, 회귀분석 결과를 비교한 값이다. 분석 결과 인공신경망 모델을 통한 예측값이 가장 적은 오차를 나타내어 실제 공사비 예측에 적합한 것으로 판단된다.
Table 9.
Validation of ANN model
Table 10.
Decision of optimized number of neurons
3.2.2 입력 변수별 민감도 분석
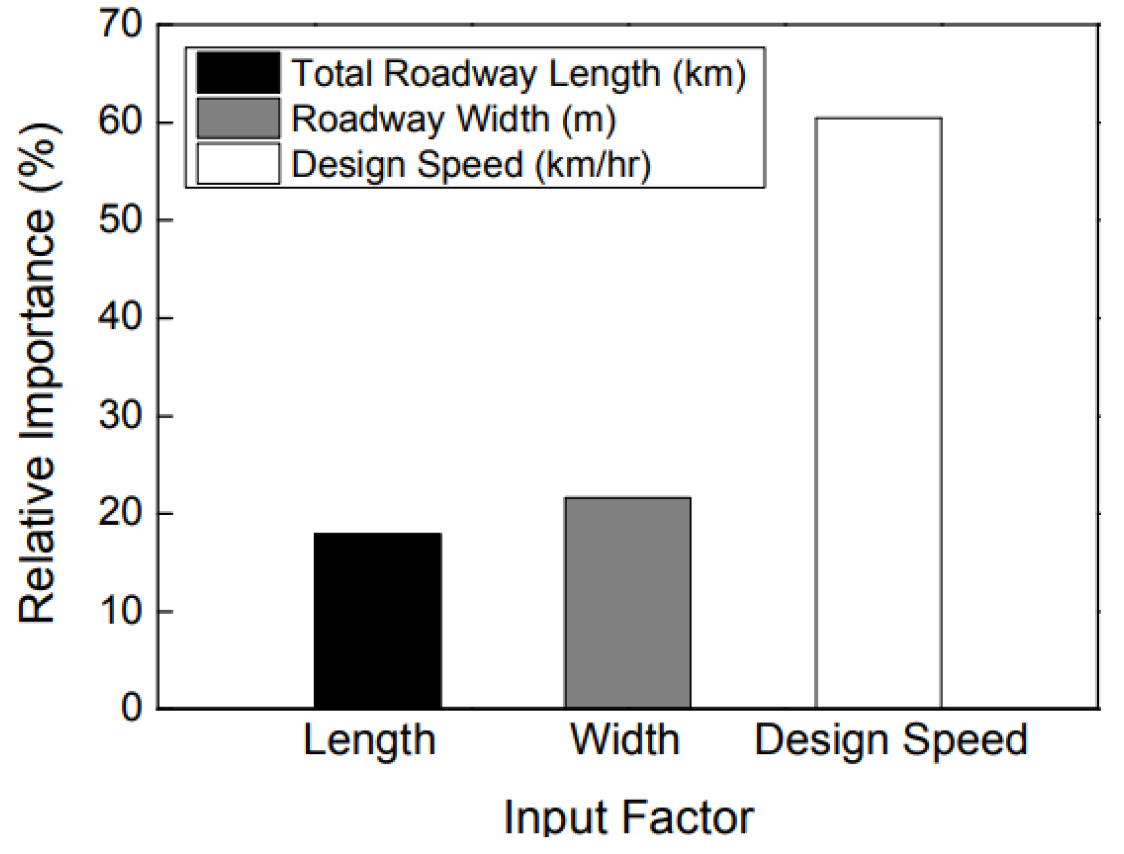
본 연구의 인공신경망 모델에 활용된 도로 총연장, 설계속도, 도로의 폭 등 입력 변수가 결과값에 미치는 상대적 중요성에 대한 민감도 분석을 실시한 결과는 Fig. 8과 같다.
분석 결과 설계속도의 상대적 중요도가 60.47%로 가장 큰 값을 나타내었으며, 도로 총연장이 가장 낮은 17.88%로 나타났다.
4. 결론 및 고찰
본 연구에서는 도로공사 계획단계에서 활용 가능한 데이터를 바탕으로 인공신경망을 통한 건설 비용 예측 모델을 제시하였으며, 최적의 모델 구축을 위한 다양한 입력변수를 조정하였고 그에 다른 도로 건설비 예측 결과를 비교 분석하였다. 구축한 인공신경망 모델은 상관계수 및 평균제곱근오차 등을 통해 검증하였으며, 본 연구를 통해 얻은 결론은 다음과 같다.
1.기존 인공신경망 연구에서 주로 사용되는 시행착오방식을 적용하여 입력변수의 종류, 은닉층 수, 뉴런 수, 학습율, 모멘텀 등을 변수로 하여 오차가 가장 적게 발생하는 건설 비용 예측 인공신경망 모델을 제안하였으며, 국토교통부에서 제시한 기준과 비교한 결과 건설 비용 예측에서 정확도가 우수함을 확인하였다.
2.상관계수 및 평균 제곱근 오차를 통한 분석 결과 도로 총연장, 도로의 폭, 설계속도를 활용한 모델이 기존 도로업무편람, 회귀식과 비교하여 실제 건설비용과 가장 유사한 결과값을 나타냄을 확인하였다.
3.인공신경망 모델에 사용된 입력변수가 예측값에 미치는 상대적 중요도를 분석한 결과 설계속도가 60.47%로 가장 컸으며, 도로 총연장이 가장 낮은 17.88%로 나타났다. 이는 설계 기준이 복잡할수록 건설비용이 증가하는 특성을 반영한 결과로 판단된다.
추후 더 많은 데이터 수집을 통한 인공신경망 모델의 정확를 향상시키고, 입력 데이터를 일반도로 및 고속도로 등으로 확대·구분하여 도로 건설비용 예측을 위한 인공신경망 모델의 성능을 높이는 방안이 모색되어야 할 것으로 판단된다.